洛谷 SP2916 GSS5 - Can you answer these queries V

题目链接

哇塞,大毒瘤题!

0x00 思路

首先你得先过了这道题,题解

我们继续维护和之前一样的:区间和/区间最大前缀和/区间最大后缀和/区间最大子段和

然后我们分类讨论秒切这题

查询区间不相交(y1 < x2)

答案Ans=最大后缀[x1,y1] + 最大前缀 [x2,y2] + 区间和 [y1+1,x2-1]

注意是闭区间

查询区间相交的情况(y1 >= x2)

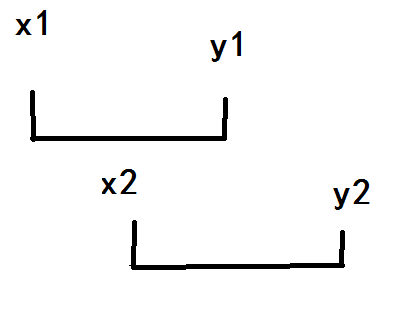
我们把查询区间分成三块\([x1,x2-1] \ [x2,y1] \ [y1+1,y2]\)

显然左端点只能在前两块内,右端点只能在后两块内

刚好分四类讨论:

设左右端点为\(L \ R\)

1. \(L \ R \in [x2,y1]\) 区间最大子段和

2. \(L \in [x1,x2-1] R \in [x2,y1]\) 区间最大后缀+区间最大前缀

3. \(L \in [x2,y1] R \in [y1+1,y2]\) 区间最大后缀+区间最大前缀

4. \(L \in [x1,x2-1] R \in [y1+1,y2]\) 区间最大后缀+区间和+区间最大前缀

综上此题我秒了

以上所有区间均要讨论是否存在,若不存在,是无法用线段树查询的

0x01 Code

#include<bits/stdc++.h>
using namespace std;
#define mid ((l+r)>>1)
#define ls (nod<<1)
#define rs (nod<<1|1)
#define lson ls,l,mid
#define rson rs,mid+1,r

int read(){
	int x=0; char c=getchar(); int flag=1;
	while(!isdigit(c)) { if(c=='-') flag=-1; c=getchar(); }
	while(isdigit(c)) { x=((x+(x<<2))<<1)+(c^48); c=getchar(); }
	return x*flag;
}

const int N=1e5+50;

int n,q;

struct Node{
    int l,r;
    int lv,rv,v;
    int sum;
}t[N<<2];

Node Union(Node a,Node b){
    Node c;
    c.l=a.l; c.r=b.r;
    c.lv=max(a.lv,a.sum+b.lv);
    c.rv=max(b.rv,b.sum+a.rv);
    c.v=max(max(a.v,b.v),a.rv+b.lv);
    c.sum=a.sum+b.sum;
    return c;
}

void pushup(int nod){
    if(t[nod].l==t[nod].r) return ;
    t[nod]=Union(t[ls],t[rs]);
}

void build(int nod,int l,int r){
    t[nod].l=l; t[nod].r=r;
    if(l==r){
	    t[nod].lv=t[nod].rv=t[nod].v=t[nod].sum=read();
	    return ;
	}
	build(lson); build(rson);
	pushup(nod);
}

Node query(int nod,int l,int r,int ll,int rr){
	if(ll>rr) {
	    Node ret;
	    ret.lv=ret.rv=ret.v=ret.sum=0;
	    return ret;
	}
	
    if(l==ll&&r==rr) return t[nod]; 
    if(rr<=mid) return query(lson,ll,rr);
    else if(ll>mid) return query(rson,ll,rr);
    else return Union(query(lson,ll,mid),query(rson,mid+1,rr));
}

signed main(){
	int T=read();
	while(T--){
	    n=read();
		build(1,1,n);
		q=read();
		while(q--){
		    int l1=read(),r1=read(),l2=read(),r2=read();
		    if(r1<l2){
		    	printf("%d\n",query(1,1,n,l1,r1).rv+query(1,1,n,l2,r2).lv+query(1,1,n,r1+1,l2-1).sum);
			}else{
				int ans=query(1,1,n,l2,r1).v;
				if(l1<l2) ans=max(ans,query(1,1,n,l1,l2-1).rv+query(1,1,n,l2,r1).lv);
				if(r1<r2) ans=max(ans,query(1,1,n,l2,r1).rv+query(1,1,n,r1+1,r2).lv);
				if(l1<l2&&r1<r2) ans=max(ans,query(1,1,n,l1,l2-1).rv+query(1,1,n,l2,r1).sum+query(1,1,n,r1+1,r2).lv);
				printf("%d\n",ans);
			    //printf("%d\n",max(,max(query(1,1,n,l2,r1).rv+query(1,1,n,r1+1,r2).lv,max(query(1,1,n,l1,l2-1).rv+query(1,1,n,l2,r1).lv,query(1,1,n,l1,l2).rv+query(1,1,n,r1,r2).lv+query(1,1,n,l2+1,r1-1).sum))));
			}
		}   
	}
    return 0;
}