降维
《机器学习系统设计》第11章 降维 学习笔记
针对书上的内容和网络上的资料记录下来的笔记,大家一起学习交流。
一.为什么需要降维
(一) 多余的特征会影响或误导学习器
(二) 更多特征意味着更多参数需要调整,过拟合风险也越大
(三) 数据的维度可能只是虚高,真实维度可能比较小
(四) 维度越少意味着训练越快,更多东西可以尝试,能够得到更好的结果
(五) 如果我们想要可视化数据,就必须限制在两个或三个维度上
因此,我们需要通过降维把无关或冗余的特征删掉。
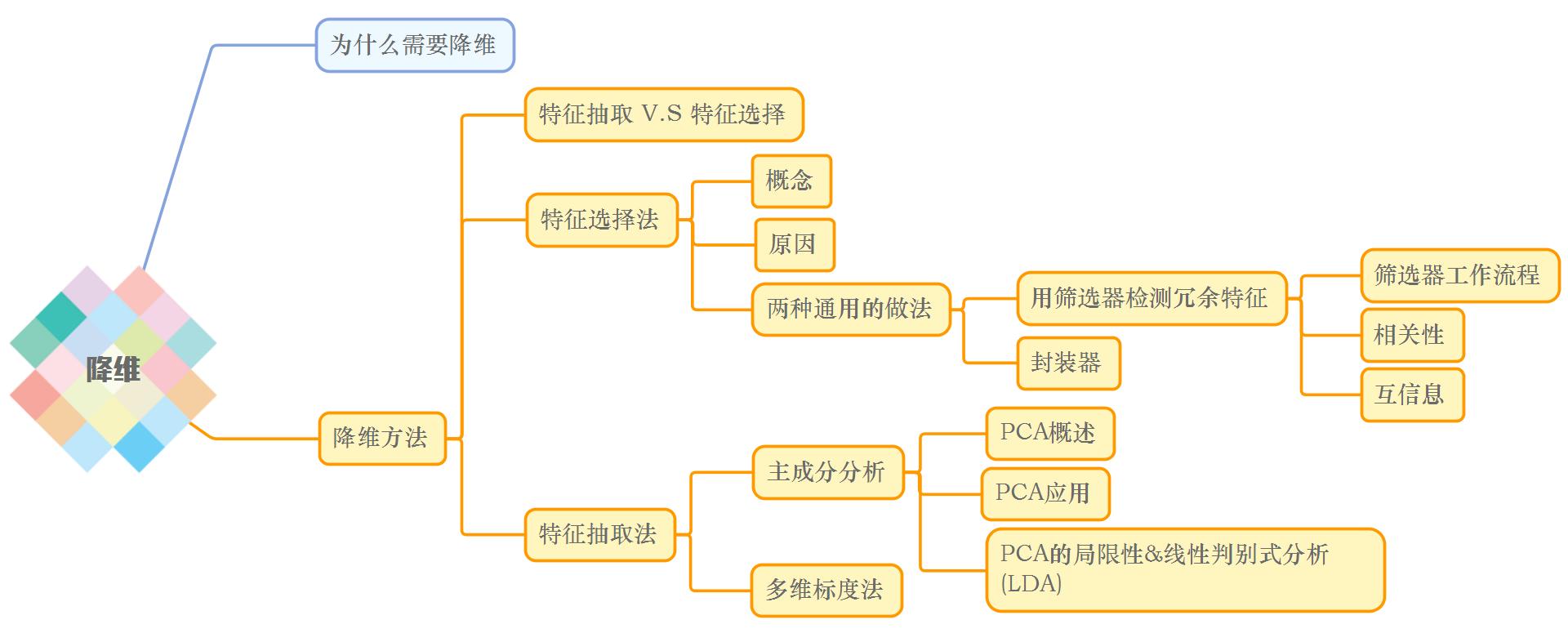
二.降维方法
(一)特征抽取 V.S 特征选择
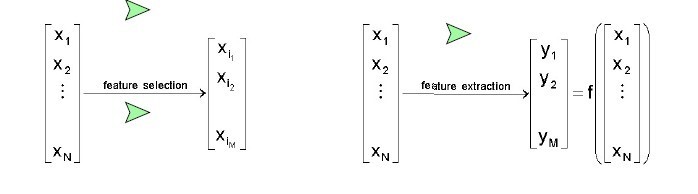
特征抽取和特征选择是降维的两种方法,针对于维数灾难(随着维数的增加,计算量呈指数倍增长的一种现象。),都可以达到降维的目的。
特征抽取(Feature Extraction):特征抽取后的新特征是原来特征的一个映射。
特征选择(Feature Selection):特征选择后的特征是原来特征的一个子集。
(二)特征选择法
1.什么是特征选择
特征选择是指从全部特征中选取一个特征子集,使构造出来的模型更好。
2.为什么要做特征选择
在机器学习的实际应用中,特征数量往往较多,其中可能存在不相关的特征,特征之间也可能存在相互依赖,容易导致如下的后果:
- 特征个数越多,分析特征、训练模型所需的时间就越长。
- 特征个数越多,容易引起“维度灾难”,模型也会越复杂,其推广能力会下降。
特征选择能剔除不相关或亢余的特征,从而达到减少特征个数,提高模型精确度,减少运行时间的目的。另一方面,选取出真正相关的特征简化了模型,使研究人员易于理解数据产生的过程。
特征选择法两种通用的做法:筛选器(filter)和封装器(wrapper)
3.用筛选器检测冗余特征
筛选器通过分析特征子集内部的特点来衡量其好坏。
(1)筛选器工作流程

(2)相关性
通过使用相关性,我们很容易看到特征之间的线性关系。
这儿采用的是scipy.stat里的pearsonr()函数,计算皮尔逊相关系数【p.s. 比集体智慧编程第三章中的皮尔逊相关系数计算代码简单多了有木有,有的包还是 很方便的。】
两个变量之间的相关系数越高,从一个变量去预测另一个变量的精确度就越高,这是因为相关系数越高,就意味着这两个变量的共变部分越多,所以从其中一个变量
的变化就可越多地获知另一个变量的变化。如果两个变量之间的相关系数为1或-1,那么你完全可由变量X去获知变量Y的值。
from scipy.stats import pearsonr pearsonr([1,2,3],[1,2,3.1]) #输出 (0.99962228516121843, 0.017498096813278487)
输出结果为(皮尔逊相关系数,p-值)

前三个具有高相关系数的情形中,我们可能要把X1或X2扔掉,因为它们似乎传递了相似的信息。然而在最后一种情况中,我们应该把两个特征都保留。
尽管这种方法在前面的例子中工作得不错,但在实际应用中却不如意。
基于相关性的特征选择方法的一个最大缺点就是:只能检测出线性关系。
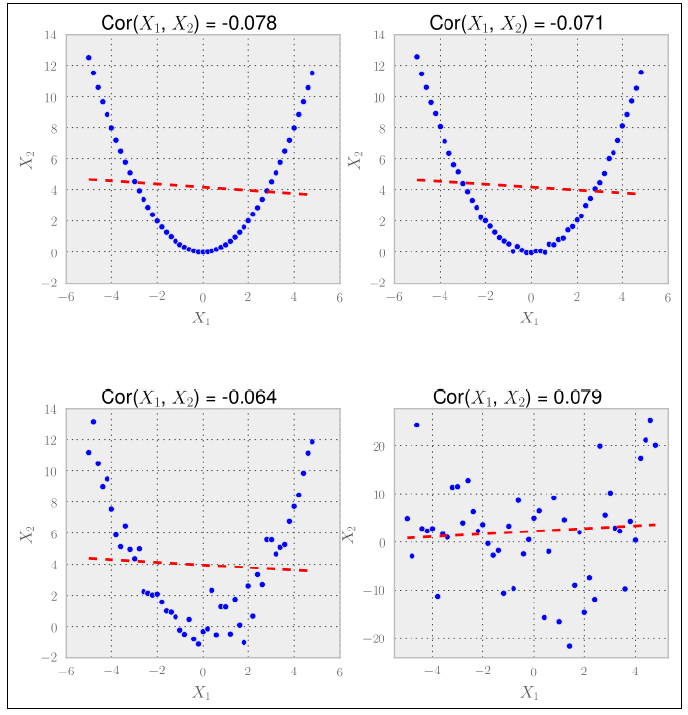
很明显,相关性在检测线性关系中是很有用的,但对于其他关系就不行了。
(3)互信息
对于非线性关系需要用到互信息。
互信息(Mutual Information)是信息论里一种有用的信息度量,它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。
要理解互信息是怎样工作的,我们需要深入理解一些信息熵的知识。
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。直到1948年,香农提出了“信息熵”的概念,才解决了对信息的量化度量问题。信息论之父 C. E. Shannon 在 1948 年发表的论文“通信的数学理论( A Mathematical Theory of Communication )”中, Shannon 指出,任何信息都存在冗余,冗余大小与信息中每个符号(数字、字母或单词)的出现概率或者说不确定性有关。
假设我们有一个公平的硬币,在旋转它之前,它是正面还是反面的不确定性是最大的,因为两种情况都有50%的概率。这种不确定性可以通过信息熵来衡量:

在公平硬币情境下,我们有两种情况令x0代表硬币正面,x1代表硬币反面,p(x0)=p(x1)=0.5
因此我们得到下面的式子:
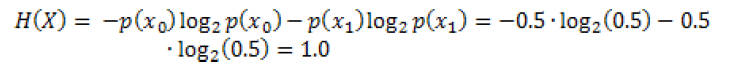
现在想象我们事先不知道这个硬币实际上并不是公平的,旋转之后有60%的可能性会出现硬币的正面:
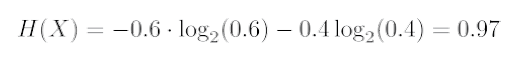
我们可以看到这种情形有较少的不确定性。不管正面出现的概率为0%还是100%,不确定性都将会远离我们在0.5时所得到的熵,到达极端的0值。
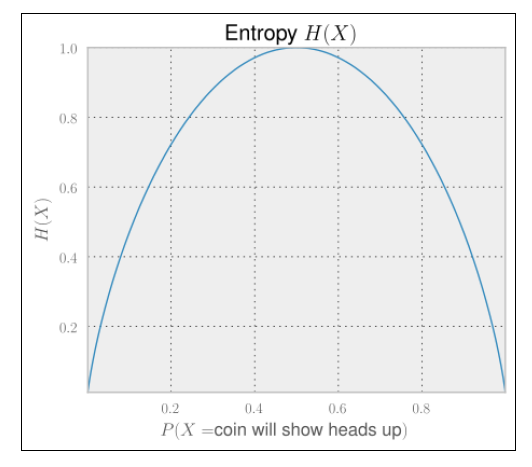

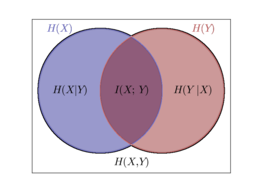
随机变量x,y之间的互信息定义为:
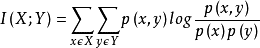

为了把互信息量限制在[0,1]区间,需要把它除以每个独立变量的信息熵之和,然后就可以得到归一化后的互信息量:
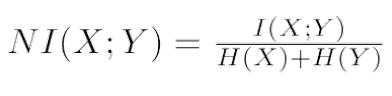
互信息量的一个较好的性质在于,跟相关性不同,它并不只关注线性关系,如下图所示:


所以,我们需要计算每一对特征的归一互信息量,对于具有较高互信息量的特征对,我们会把其中一个特征扔掉。
在介绍封装器之前插播一个Scikit-learn的小介绍
scikit-learn是Python的一个开源机器学习模块,它建立在NumPy,SciPy和matplotlib模块之上。
scikit-learn最大的特点就是,为用户提供各种机器学习算法接口,可以让用户简单、高效地进行数据挖掘和数据分析。
安装方法:
pip install scikit-learn
安装scikit-learn可能会提示你电脑需要装Microsoft Visual C++ 9.0,解决方法就是利用下边的网址安装好Microsoft Visual C++ Compiler for Python 2.7,即可pip install scikit-learn
(四)用封装器让模型选择特征
封装器实质上是一个分类器,封装器用选取的特征子集对样本集进行分类,分类的精度作为衡量特征子集好坏的标准。
- 封装器工作流程图
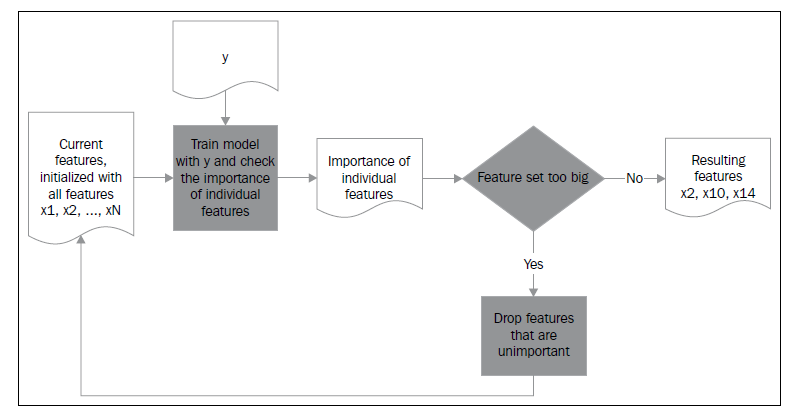
在sklearn.feature_selection包里有各种优秀的封装器类。这个领域中的一个真正的主力军叫做RFE(特征递归消除 recursive feature elimination)。它会把一个估算其和预期数量的特征当做参数,然后只要发现一个足够小的特征子集,就在这个特征集合里训练估算器。
例子:通过datasets的make_classification()函数,创建了一个人工构造的分类问题。它包含100个样本,我们创建了10个特征,其中只有3个对解决这个分类问题是有价值的。
# -*- coding:utf-8 -*- from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression from sklearn.datasets import make_classification X,y = make_classification(n_samples=100,n_features=10,n_informative=3,random_state=0) #make_classification:Generate a random n-class classification problem创建一个随机的分类问题 clf = LogisticRegression()#Logistic回归是一个线性分类器。LogisticRegression实现了该分类器 clf.fit(X,y) #拟合模型 selector = RFE(clf,n_features_to_select=3)#特征递归消除 selector = selector.fit(X,y)#拟合 print selector.support_ print selector.ranking_ #输出 [False True False True True False False False False False] [7 1 4 1 1 3 2 8 6 5]
(三)特征抽取法

1.主成分分析(PCA)
(1)PCA概述
PCA主要 用于数据降维,对于一系列例子的特征组成的多维向量,多维向量里的某些元素本身没有区分性,比如某个元素在所有的例子中都为1,或者与1差距不大,那么这个元素本身就没有区分性,用它做特征来区分,贡献会非常小。所以我们的目的是找那些变化大的元素,即方差大的那些维,而去除掉那些变化不大的维,从而使特征留下的都是精品,而且计算量也变小了。
(2)PCA应用
基于 Python 中 sklearn 模块的 PCA 算法实现
#创建人造数据集 import numpy as np x1 = np.arange(0,10,.2) #arange([start,] stop[, step,], dtype=None) #Return evenly spaced values within a given interval. #起点,终点,步长值。含起点值,不含终点值 x2 = x1+np.random.normal(loc=0,scale=1,size=50) #normal(loc=0.0, scale=1.0, size=None) #Draw random samples from a normal (Gaussian) distribution. #均值,标准差,生成的随机数的个数 X=np.c_[(x1,x2)] #np.r_按row来组合array, #np.c_按colunm来组合array
##创建分类 good = (x1>5)|(x2>5) #x1大于5或x2大于5 bad = ~good #~为取反
##主成分分析 from sklearn import linear_model,decomposition,datasets pca = decomposition.PCA(n_components=1) #把数据降为1个维度 #sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False) '''n_components: 类型:int 或者 string,缺省时默认为None,所有成分被保留。 赋值为int,比如n_components=1,将把原始数据降到一个维度。 赋值为string,比如n_components=‘mle‘,将自动选取特征个数n,使得满足所要求的方差百分比。 意义:PCA算法中所要保留的主成分个数n,也即保留下来的特征个数n copy: 类型:bool,True或者False,缺省时默认为True。 意义:表示是否在运行算法时,将原始训练数据复制一份。若为True,则运行PCA算法后,原始训练数据的值不会有任何改变,因为是在原始数据的副本上进行运算;若为False,则运行PCA算法后,原始训练数据的值会改,因为是在原始数据上进行降维计算。 whiten: 类型:bool,缺省时默认为False 意义:白化,使得每个特征具有相同的方差。''' Xtrans = pca.fit_transform(X) #pca.fit_transform(X):用X来训练PCA模型,同时返回降维后的数据。
print pca.explained_variance_ratio_ #查看在变换中保留下来的数据方差 #output [ 0.9663034]
这意味着,例子中在数据从二维变成一维之后,我们仍然剩下96%的方差
####其它参数解释
PCA对象的属性
components_ :返回具有最大方差的成分。
explained_variance_ratio_:返回 所保留的n个成分各自的方差百分比。
n_components_:返回所保留的成分个数n。
PCA对象的方法
fit(X,y=None)
fit()可以说是scikit-learn中通用的方法,每个需要训练的算法都会有fit()方法,它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法,此处y自然等于None。fit(X),表示用数据X来训练PCA模型。函数返回值:调用fit方法的对象本身。比如pca.fit(X),表示用X对pca这个对象进行训练。用X来训练PCA模型,同时返回降维后的数据。
- fit_transform(X)
newX=pca.fit_transform(X),newX就是降维后的数据。将降维后的数据转换成原始数据,X=pca.inverse_transform(newX)
- inverse_transform()
将数据X转换成降维后的数据。当模型训练好后,对于新输入的数据,都可以用transform方法来降维。
- transform(X)
3.PCA的局限性&线性判别式分析(LDA)
作为一个线性方法,PCA在处理非线性数据时就有局限性了。
LDA与PCA的一大不同点在于,LDA是有监督的算法,而PCA是无监督的,因为PCA算法没有考虑数据的标签(类别),只是把原数据映射到一些方差比较大的方向上去而已,而LDA算法则考虑了数据的标签。
import numpy as np x1 = np.arange(0,10,.2) x2 = x1+np.random.normal(loc=0,scale=1,size=50) X=np.c_[(x1,x2)] good =x1>x2 bad = ~good
from sklearn import lda lda_inst = lda.LDA(n_components=1) Xtrans = lda_inst.fit_transform(X,good)
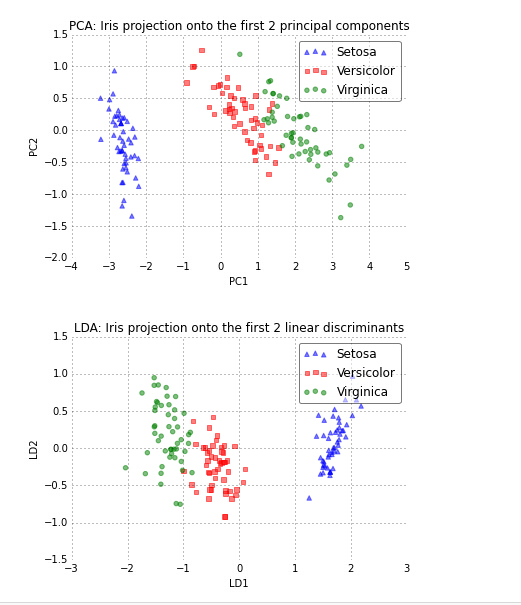
使用PCA和LDA同时对样本集合X进行降维,都降至2维,得到的散点图如下:
可以看出,对于PCA降维后的样本散点图来说,其整体样本沿着X轴的方差最大,而沿着Y轴的方差次大。
而从LDA图可以看出,X轴方向对各类样本的区分度最好,而Y轴对各类样本的区分度次好。
所以可以看出,如果仅仅用于分类的话,LDA降维的效果要比PCA好一些。PCA更适合于解释样本在不同方向上的变化幅度大小。
(二)多维标度法(MDS)
一方面,PCA试图对保留下来的数据方差进行优化,而另一方面,MDS在降低维度的时候试图尽可能保留样本间的相对距离。当我们有一个高维数据集,并希望获得一个视觉印象的时候,这是非常有用的。
多维标度法的目标:当n个对象总各对对象之间的相似性(或距离)给定时,确定这些对象在低维空间中的表示,并使其尽可能原先的相似性“大体匹配”,使得由降维引起的任何变形达到最小。
import numpy as np x1 = np.arange(0,10,.2) x2 = x1+np.random.normal(loc=0,scale=1,size=50) X=np.c_[(x1,x2)] good =x1>x2 bad = ~good from sklearn import manifold mds = manifold.MDS(n_components=3) Xtrans = mds.fit_transform(X)