DS博客作业05--查找
0.PTA得分截图

1.本周学习总结
1.1 总结查找内容
静态查找算法的查找性能指标ASL
顺序查找
-
算法思路
从表的一端开始,顺序扫描线性表,依次将扫描到的关键字和给定值k相比较,若当前扫描到的关键字与k相等,则查找成功;若扫描结束后,仍未找到关键字等于k的记录,则查找失败。 -
顺序查找的算法如下(在顺序表R[0..n-1]中查找关键字为k的元素,成功时返回找到的元素的逻辑序号,失败时返回0)
int SeqSearch(SeqList R,int n,KeyType k)
{
int i=0;
while (i<n && R[i].key!=k) //从表头往后找
i++;
if (i>=n) //未找到返回0
return 0;
else
return i+1;//找到返回逻辑序号i+1
}
-
查找性能指标ASL分析

-
成功时的顺序查找的平均查找长度为:
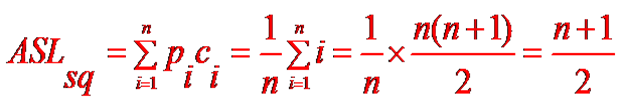
-
查找成功时的平均查找长度:(n+1)/2,即约为表长的一半。
-
查找不成功时的平均查找长度:n,需要查找一整个顺序表
-
二分查找
-
二分查找也称为折半查找,要求线性表中的节点必须己按关键字值的递增或递减顺序排列。
-
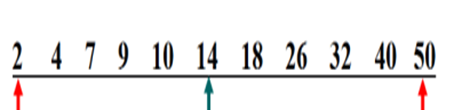
二分查找举例如下
在关键字有序序列{2,4,7,9,10,14,18,26,32,40,50}中采用二分查找法查找关键字为9的元素。

-
二分查找的算法如下
int BinSearch(SeqList R,int n,KeyType k)
{ //迭代版
int low=0,high=n-1,mid;
while (low<=high) //当前区间存在元素时循环
{
mid=(low+high)/2;
if (R[mid].key==k) //查找成功
return mid+1;
if (k<R[mid].key)
high=mid-1;
else
low=mid+1;
}
return 0;
}
int BinSearch1(SeqList R,int low,int high,KeyType k)
{ //递归版
int mid;
if (low<=high) //查找区间存在一个及以上元素
{
mid=(low+high)/2; //求中间位置
if (R[mid].key==k) //查找成功返回其逻辑序号mid+1
return mid+1;
if (R[mid].key>k) //在R[low..mid-1]中递归查找
BinSearch1(R,low,mid-1,k);
else //在R[mid+1..high]中递归查找
BinSearch1(R,mid+1,high,k);
}
else return 0;
}
二分查找的性能分析-判定树
-
二分查找的判定树或比较树定义:
- 把当前查找区间的中间位置上的记录作为根;
- 左子表和右子表中的记录分别作为根的左子树和右子树。
-
以下面的一棵判定树为例计算成功与不成功时的ASL
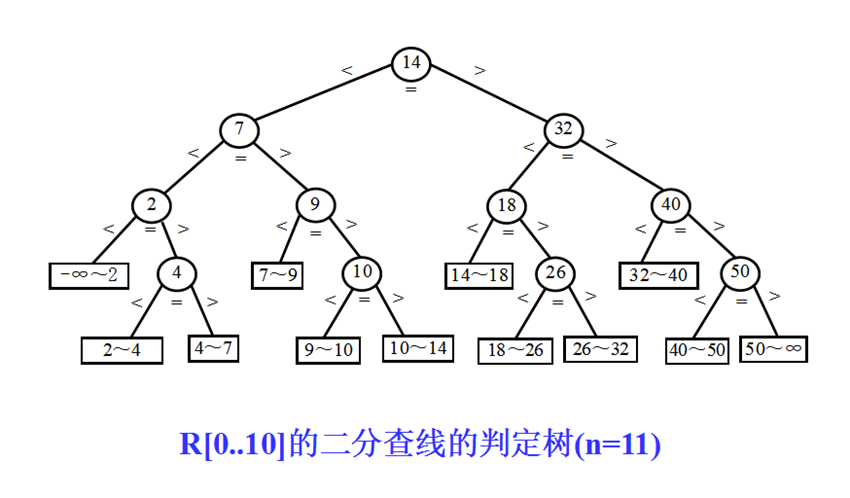
-
(其中,矩形:外部节点不成功对应序号范围;圆形:内部节点)
-
在查找成功时,会找到图中某个圆形节点,则成功时的平均查找长度:
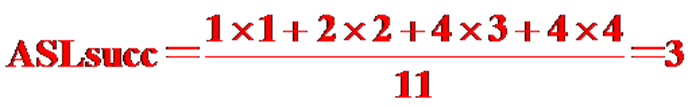
-
在查找不成功时,会找到图中某个方形节点,则不成功时的平均查找长度:
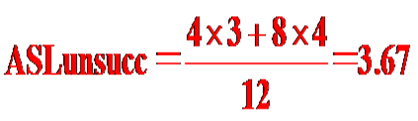
-
二分查找的平均查找长度
- 树中第i层上的记录个数为2i-1,查找该层上的每个记录需要进行i次比较。
- 当n比较大时,判定树看成内部节点的总数为n=2h-1、高度为h=log2(n+1)的满二叉树


- 二分查找的ASL成功和ASL失败还是应该通过画出对应查找序列的判定树,进而进行计算。
动态查找:二叉搜索树
二叉搜索树定义:
- 或者是一棵空树;或者是具有如下特性的二叉树,
- 若它的左子树不空,则左子树上所有结点的值均小于根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于根结点的值;
- 它的左、右子树也都分别是二叉排序树。
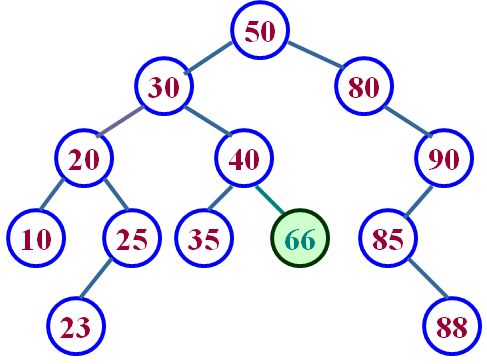
- 如上的一棵树就不是二叉排序树(根节点的左子树中的节点66大于根节点50)
- 注意:二叉排序树中没有相同关键字的节点。
二叉排序树的特点
-
根结点的最左下结点是关键字最小的结点
-
根结点的最右下结点是关键字最大的结点
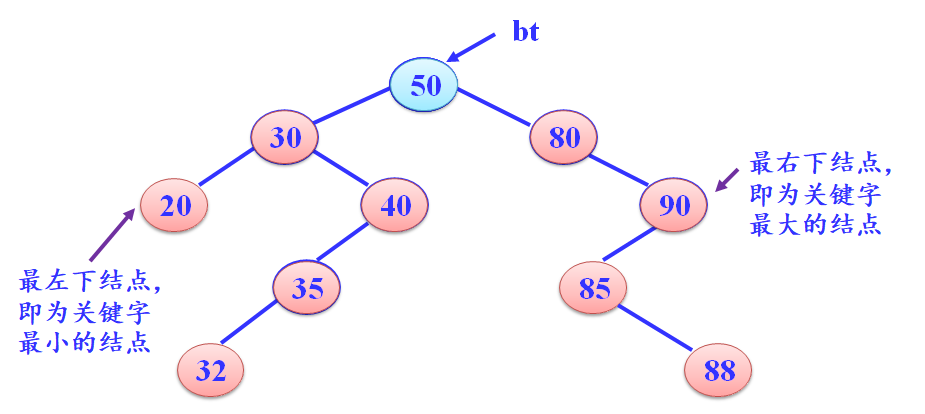
-
二叉排序树的中序序列是一个递增有序序列

二叉搜索树的结点结构体:
typedef struct node
{ KeyType key; //关键字项
InfoType data; //其他数据域
struct node *lchild,*rchild; //左右孩子指针
} BSTNode,*BSTree;
1、二叉排序树的插入和生成
- 在二叉排序树中插入一个关键字为k的新结点,要保证插入后仍满足BST性质。
- 若二叉排序树T为空,则创建一个key域为k的结点,将它作为根结点;否则将k和根结点的关键字比较。
- 若两者相等,则说明树中已有此关键字k,无须插入,直接返回0;
- 若k
key,则将k插入根结点的左子树中。 - 否则将它插入右子树中。
BSTNode *CreatBST(KeyType A[],int n) //返回树根指针
{ BSTNode *bt=NULL; //初始时bt为空树
int i=0;
while (i<n)
{
InsertBST(bt,A[i]); //将A[i]插入二叉排序树T中
i++;
}
return bt; //返回建立的二叉排序树的根指针
}
int InsertBST(BSTree &p,KeyType k)
{
if (p==NULL) //原树为空
{
p=new BSTNode;
p->key=k;p->lchild=p->rchild=NULL;
return 1;
}
else if (k==p->key) //相同关键字的节点0
return 0;
else if (k<p->key)
return InsertBST(p->lchild,k); //插入到左子树
else
return InsertBST(p->rchild,k); //插入到右子树
}
2. 二叉排序树上的查找(Binary Sort Tree)
- 因为二叉排序树可看做是一个有序表,所以在二叉排序树上进行查找,和二分查找类似。
BSTNode *SearchBST(BSTNode *bt,KeyType k) //递归版
{
if (bt==NULL || bt->key==k) //递归终结条件
return bt;
if (k<bt->key)
return SearchBST(bt->lchild,k); //在左子树中查找
else
return SearchBST(bt->rchild,k); //右子树中查找
}
BSTNode *SearchBST1(BSTNode *bt,KeyType k)
{ //迭代版
while (bt!=NULL)
{
if (k==bt->key)
return bt;
else if (k<bt->key)
bt=bt->lchild; //在左子树中迭代查找
else
bt=bt->rchild; //在左子树中迭代查找
}
return NULL; //没有找到返回NULL
}
- 查找最大节点
KeyType maxnode(BSTNode *p)
//返回一棵二叉排序树中最大节点关键字
{
while (p->rchild!=NULL)
p=p->rchild;
return(p->data);
}
- 查找最小节点
KeyType minnode(BSTNode *p)
//返回一棵二叉排序树中的最小节点关键字
{
while (p->lchild!=NULL)
p=p->lchild;
return(p->data);
}
3.二叉排序树的节点删除
-
分为如下情况:
- 被删除的节点是叶子节点。
- 被删除的节点只有左子树或者只有右子树
- 被删除的节点既有左子树,也有右子树。
-
被删除的节点是叶子节点:直接删去该节点

-
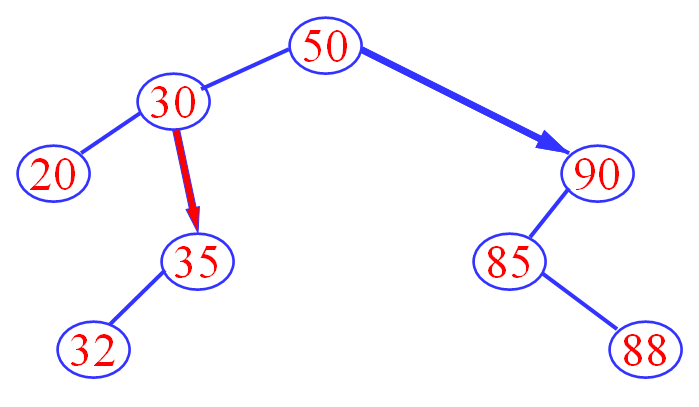
被删除的节点只有左子树或者只有右子树,用其左子树或者右子树代替它
-
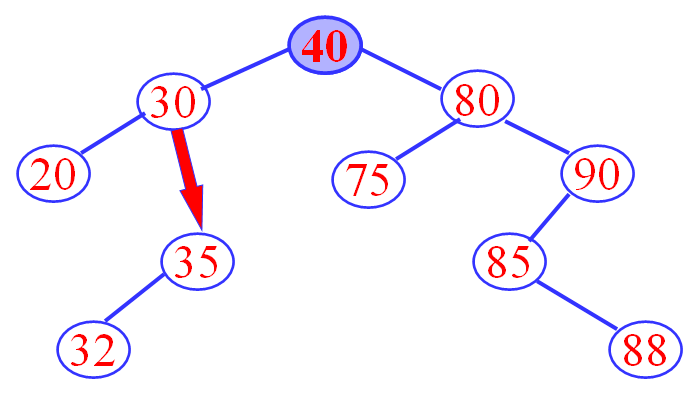
被删除的节点既有左子树,也有右子树。
- 以其前驱替代之,然后再删除该前驱节点。前驱是左子树中最大的节点。
- 也可以用其后继替代之,然后再删除该后继节点。后继是右子树中最小的节点。
-
具体实现代码如下
int DeleteBST(BSTree &bt,KeyType k)
{
if (bt==NULL) return 0; //空树删除失败
else
{
if (k<bt->key) return DeleteBST(bt->lchild,k); //递归在左子树中删除为k的节点
else if (k>bt->key) return DeleteBST(bt->rchild,k); //递归在右子树中删除为k的节点
else
{
Delete(bt); //删除*bt节点
return 1;
}
}
}
void Delete(BSTreee &p) //从二叉排序树中删除*p节点
{
BSTNode *q;
if (p->rchild==NULL) //*p节点没有右子树的情况
{
q=p; p=p->lchild;delete q;
}
else if (p->lchild==NULL) //*p节点没有左子树
{
q=p; p=p->rchild;delete q;
}
else Delete1(p,p->lchild); //*p节点既有左子树又有右子树的情况
}
void Delete1(BSTNode *p,BSTNode *&r) //被删节点:p,p的左子树节点:r
{
BSTNode *q;
if (r->rchild!=NULL)
Delete1(p,r->rchild); //递归找最右下节点
else //找到了最右下节点*r
{ //将*r的关键字值赋给*p
p->key=r->key;
q=r; r=r->lchild;delete q;
}
}
AVL树的定义及4种调整做法
平衡二叉树(又称AVL树)定义
- 左、右子树是平衡二叉树;
- 所有结点的左、右子树深度之差的绝对值(平衡因子)≤ 1
- 平衡因子:该结点左子树与右子树的高度差
AVL树的节点结构体定义如下
typedef struct node //记录类型
{
KeyType key; //关键字项
int bf; //增加的平衡因子
InfoType data; //其他数据域
struct node *lchild,*rchild; //左右孩子指针
} BSTNode;
- 如果在一棵AVL树中插入一个新结点,就有可能造成失衡,此时必须重新调整树的结构,使之恢复平衡。我们称调整平衡过程为平衡旋转,包括:
- LL平衡旋转
- RR平衡旋转
- LR平衡旋转
- RL平衡旋转
- 进行平衡旋转是为了保证AVL树仍然是排序树
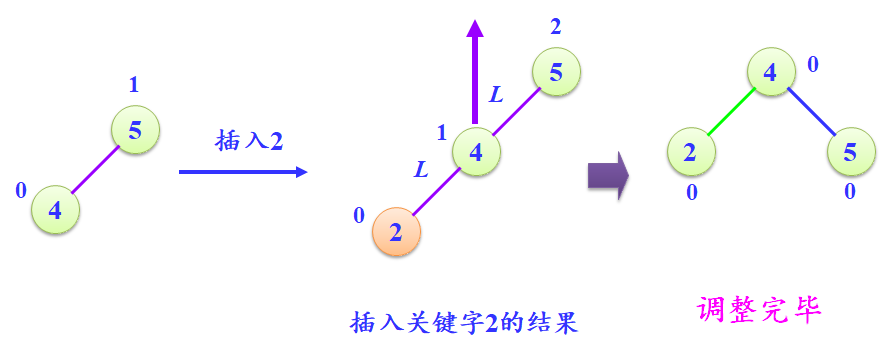
LL型调整
- 若在A的左子树的左子树上插入结点,使A失衡,平衡因子2,需要进行一次顺时针旋转。
- 1.A的左孩子B右上旋转作为A的根节点
- 2.A节点右下旋转称为B的右孩子
- 3.B原右子树称为A左子树
- AVL树LL调整演示
RR型调整
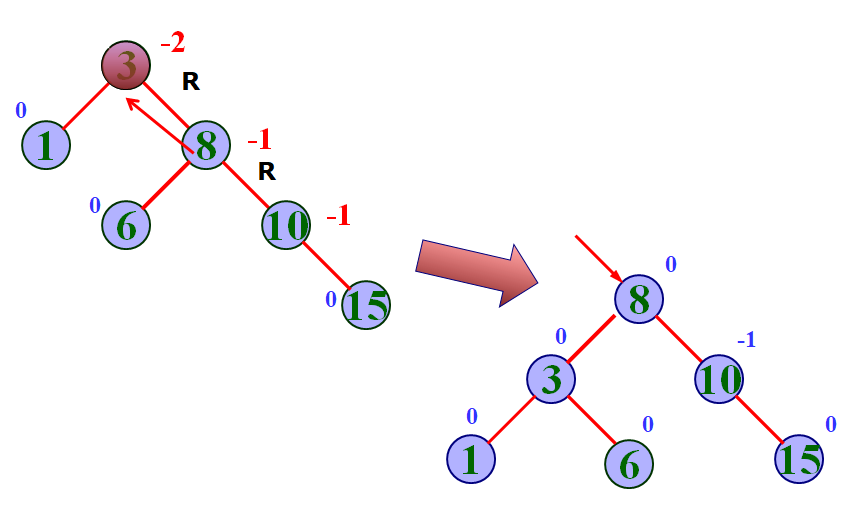
- 若在A的右子树的右子树上插入结点,使A的平衡因子从-1增加至-2,需要进行一次逆时针旋转
- 1.A的右孩子B左上旋转作为A的根节点
- 2.A节点左下旋转称为B的左孩子
- 3.B原左子树称为A右子树
- AVL树RR调整演示
LR型调整
- 若在A的左子树的右子树上插入结点,使A的平衡因子从1增加至2,(以插入的结点C为旋转轴),先C进行逆时针旋转,A再顺时针旋转。
- 1.C向上旋转到A的位置,A作为C右孩子
- 2.C原左孩子作为B的右孩子
- 3.C原右孩子作为A的左孩子
- AVL树LR调整演示
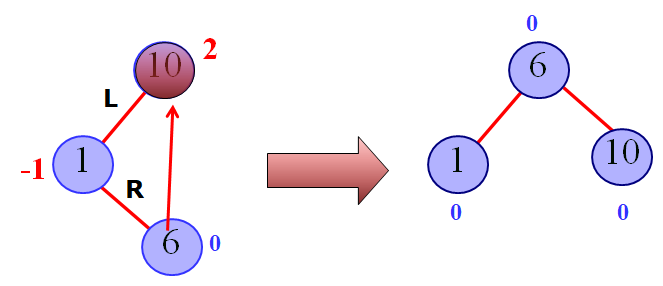
RL型调整
-
若在A的右子树的左子树上插入结点,使A的平衡因子从-1增加至-2,(以插入的结点C为旋转轴),先进行顺时针旋转,再逆时针旋转。
- 1.C向上旋转到A的位置,A作为C左孩子
- 2.C原左孩子作为A的右孩子
- 3.C原右孩子作为B的左孩子
-
AVL树LR调整演示
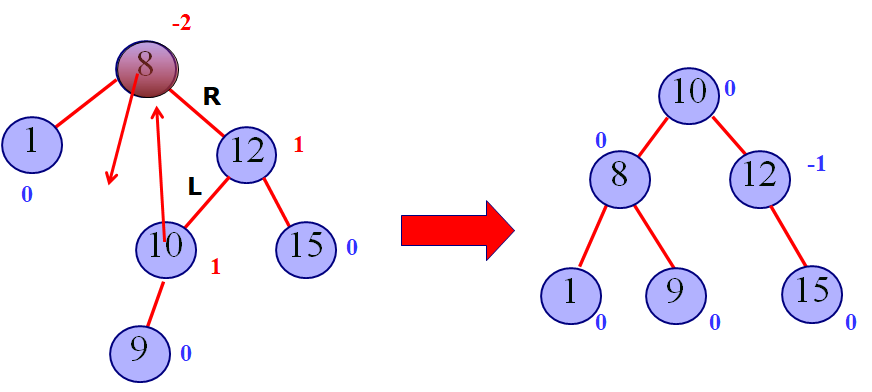
-
总结
- 多个失衡点,从最下面失衡点开始调整
- 了解是哪种失衡,谁是失衡点
- LL和RR是选择失衡点的L或R孩子旋转;LR和RL选择失衡点的相应的LR或RL孙子旋转。
- 每次调整后,检查是否二叉排序树。还有失衡点否。
B-树和B+树
B-树定义
- 一棵m阶B-树或者是一棵空树,或者是满足下列要求的m叉树:
- 每个节点至多m个孩子节点(至多有 m-1 个关键字)
- 除根节点外,其他节点至少有 m/2 个孩子节点(即至少有m/2-1 个关键字);
- 若根节点不是叶子节点,根节点至少两个孩子节点
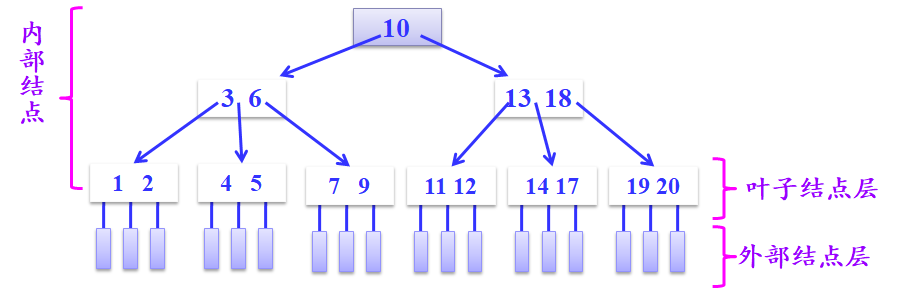
B-树中每个节点的结构为:
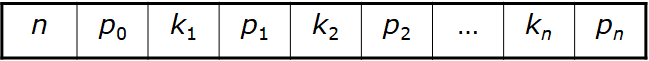
- 1.n为关键字个数,n+1孩子指针。
- 2.结点中按关键字大小顺序排列,ki<ki+1;
- 3.pi为该节点的孩子指针,满足
- p0 指向节点关键字<k0
- pi指向节点关键字大于等于[ki,ki+1]
- pn指向节点关键字>kn
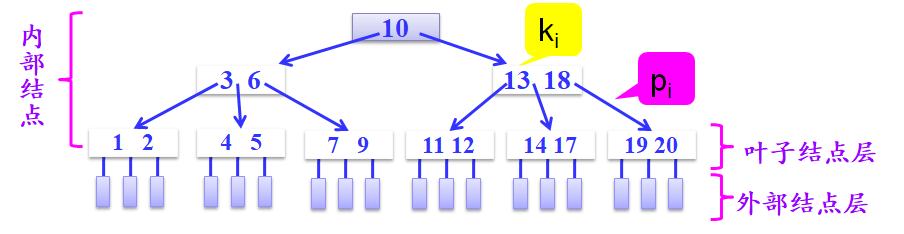
m阶B-树结点特点
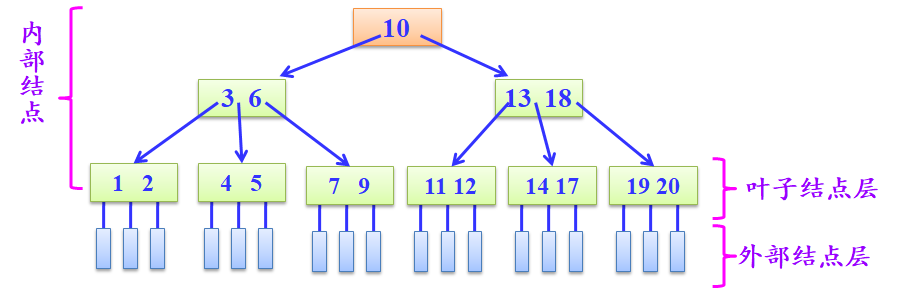
- 非根结点的孩子个数
- 最小:m/2
- 最大:m
- 非根结点的关键字个数
- 最小:m/2-1
- 最大:m-1
- 根节点至少2个孩子:2--m
- B-树是所有结点的平衡因子均等于0的多路查找树。所有外部结点都在同一层上。
- 在计算B-树的高度时,需要计入最底层的外部结点
- 外部结点就是失败结点,指向它的指针为空,不含有任何信息,是虚设的。一棵B树中总有n个关键字,则外部结点个数为n+1。
在B-树的存储结构中,各节点的类型定义如下:
#define MAXM 10 //定义B-树的最大的阶数
typedef int KeyType; //KeyType为关键字类型
typedef struct node //B-树节点类型定义
{
int keynum; //节点当前拥有的关键字的个数
KeyType key[MAXM]; //[1..keynum]存放关键字,[0]不用
struct node *parent; //双亲节点指针
struct node *ptr[MAXM];//孩子节点指针数组[0..keynum]
} BTNode;
在B-树查找结果返回如下类型:
typedef struct
{
BTNode *pt; // 指向找到的结点的指针
int i; // 1..m-1,在结点中的关键字序号
int tag; // 标志查找成功(=1)或失败(=0)
} Result; // 在B树的查找结果类型
1.B-树的查找
- 在一棵B-树上顺序查找关键字为k的方法为:
- 将k与根节点中的key[i]进行比较:
- 若k=key[i],则查找成功;
- 若k<key[1],则沿着指针ptr[0]所指的子树继续查找;
- 若key[i]<k<key[i+1],则沿着指针ptr[i]所指的子树继续查找;
- 若k>key[n],则沿着指针ptr[n]所指的子树继续查找。
- 将k与根节点中的key[i]进行比较:
- 说明:查找到某个叶结点,若相应指针为空,落入一个外部结点,表示查找失败。
2.B-树的插入:
-
在查找不成功之后,需进行插入。关键字插入的位置必定在叶子结点层,有下列几种情况:
- 该结点的关键字个数 n<m-1 ,不修改指针;
- 该结点的关键字个数 n=m-1 ,则需进行“结点分裂”
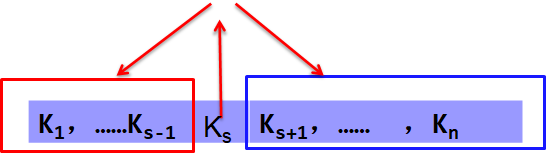
-
结点分裂
- 1.如果没有双亲结点,新建一个双亲结点,树的高度增加一层。
- 2.如果有双亲结点,将ki插入到双亲结点中。
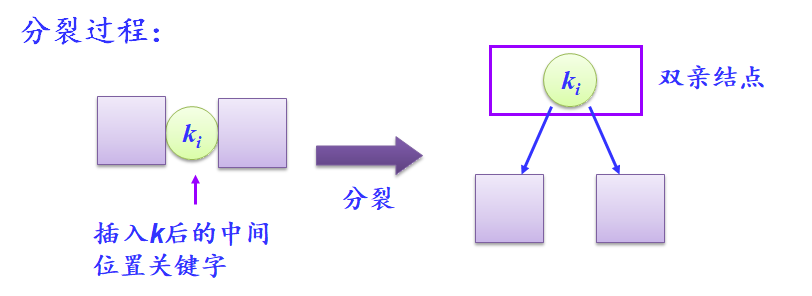
3.B树的删除
-
删除关键字k分两种情况:
- 在叶子结点层上删除关键字k。
- 在非叶子结点层上删除关键字k。
-
注意:非根、非叶子结点的关键字最少个数Min=m/2-1
-
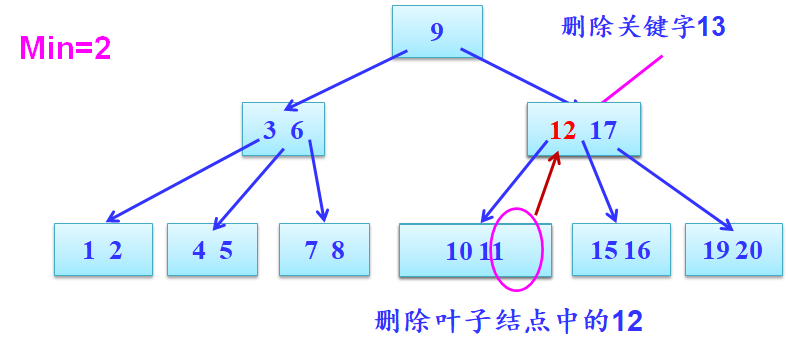
B树非叶子节点删除
- 1.从pi子树节点借调最大或最小关键字key代替ki。
- 2.pi子树中删除key
- 3.若子树节点关键字个数< m/2-1,重复步骤1
-
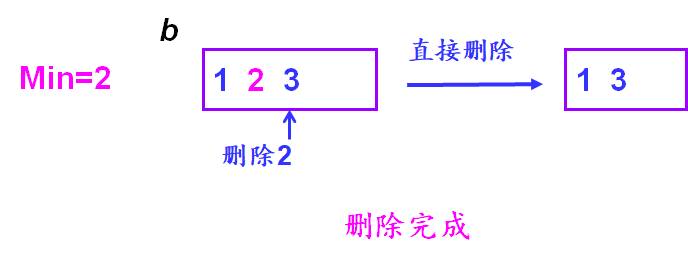
B树叶子节点删除
-
假如b结点的关键字个数大于Min,说明删去该关键字后该结点仍满足B树的定义,则可直接删去该关键字。
-
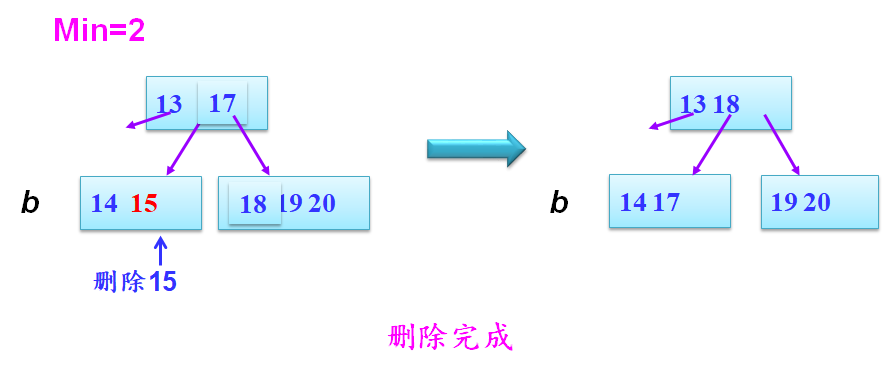
假如b结点的关键字个数等于Min,说明删去关键字后该结点将不满足B树的定义。若可以从兄弟结点借。
- 1.兄弟结点最小关键字上移双亲结点
- 2.双亲结点大于删除关键字的关键字下移删除结点
-
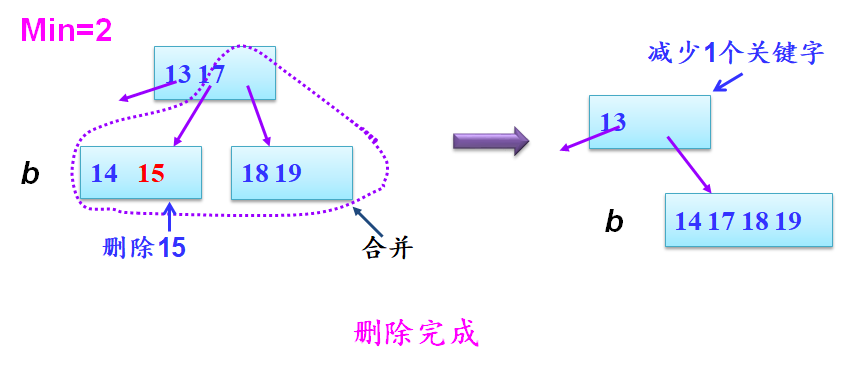
结点的关键字个数等Min,兄弟节点关键字个数也等于Min
- 1.删除关键字
- 2.兄弟节点及删除关键字节点、双亲结点中分割二者关键字合并一个新叶子结点
- 3.若双亲结点关键字个数<=Min,重复2
-
B+树
- 索引文件组织中,经常使用B-树的变形B+树。B+树是大型索引文件的标准组织方式。
- 一棵m阶B+树满足下列条件:
- 1.每个分支节点至多有m棵子树。
- 2.根节点或者没有子树,或者至少有两棵子树
- 3.除根节点,其他每个分支节点至少有m/2棵子树
- 4.有n棵子树的节点有n个关键字。
- 5.所有叶子节点包含全部关键字及指向相应记录的指针
- 叶子节点按关键字大小顺序链接
- 叶子节点是直接指向数据文件中的记录。
- 6.所有分支节点(可看成是分块索引的索引表)
- 包含子节点最大关键字及指向子节点的指针。
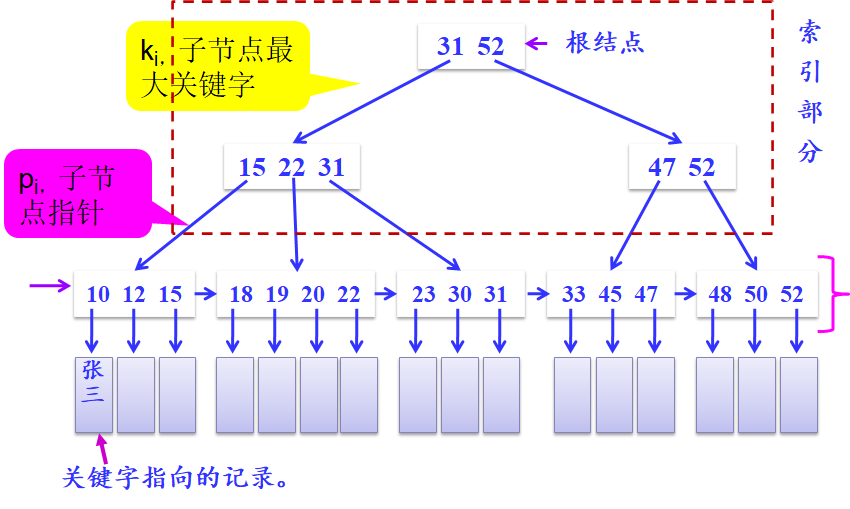
- 包含子节点最大关键字及指向子节点的指针。
B+树的查找
- 直接从最小关键字开始进行顺序查找所有叶节点链接成的线性链表。
- 从B+树的根节点出发一直找到叶节点为止。
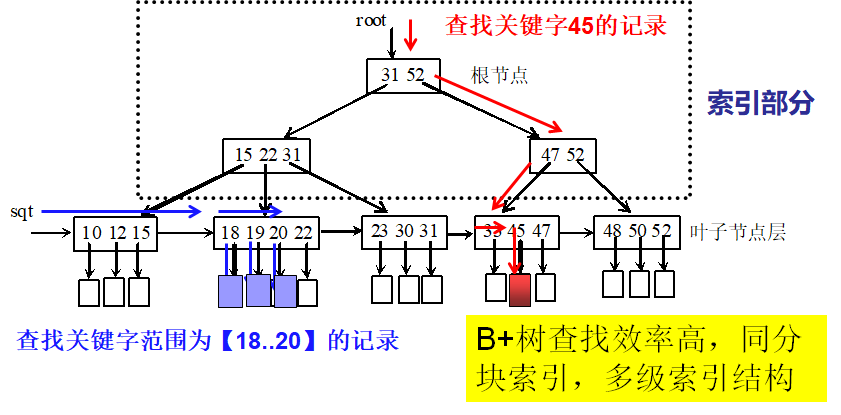
m阶的B+树和m阶的B-树的差异
- 非根结点关键字个数n不同、n取值范围不同
- B+树中:一个节点n个孩子则对应n个关键字
- 取值范围:m/2≤n≤m,根节点是1≤n≤m;
- B-树中:一个节点n个孩子则对应n-1个关键字
- 取值范围:m/2-1≤n≤m-1 ,根节点1≤n≤m-1
- 根节点孩子至少为2.
- 叶子结点不一样
- B+树所有叶子节点包含了全部关键字
- B-树叶子节点包含的关键字与其他节点包含的关键字是不重复的。
- B+树中所有非叶子节点仅起到索引的作用,而在B-树中,每个关键字对应一个记录的存储地址
- 通常在B+树上有两个头指针,一个指向根节点,另一个指向关键字最小的叶子节点,所有叶子节点链接成一个不定长的线性链表。
散列查找
哈希表(Hash Table)
-
又称散列表,是除顺序表存储结构、链接表存储结构和索引表存储结构之外的又一种存储线性表的存储结构。
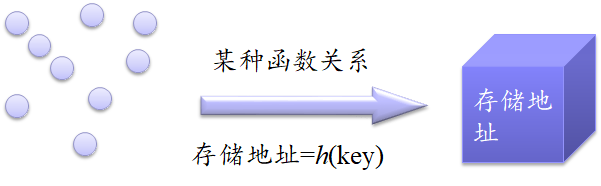
-
注意:哈希表是一种存储结构,它并非适合任何情况,主要适合记录的关键字与存储地址存在某种函数关系的数据。
哈希函数和哈希地址
- 哈希函数h(key):把关键字为ki的对象存放在相应的哈希地址中
- 哈希表:存储数据记录的长度为m(m≥n)的连续内存单元
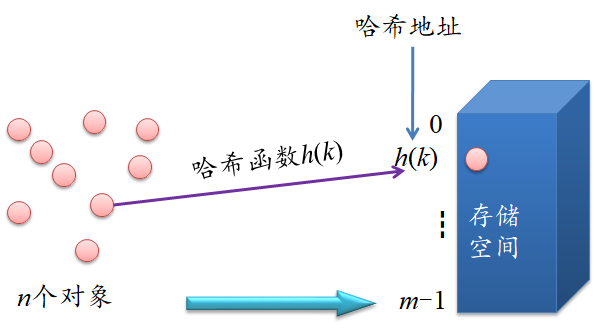
哈希冲突
- 对于两个关键字分别为ki和kj(i≠j)的记录,有ki≠kj,但h(ki)=h(kj)。把这种现象叫做哈希冲突(同义词冲突)。在哈希表存储结构的存储中,哈希冲突是很难避免的!!!
哈希表设计
- 哈希表设计主要需要解决哈希冲突。实际中哈希冲突是难以避免的,主要与3个因素有关:
- 哈希表长度
- 与装填因子有关。
- 装填因子α=存储的记录个数/哈希表的大小=n/m
- α越小,冲突可能性就越小;α越大(最大可取1),冲突的可能性就越大。控制在0.6~0.9的范围内
- 与所采用的哈希函数有关。
- 与解决冲突方法有关。
- 哈希表长度
哈希函数构造方法
-
1. 直接定址法
- 直接定址法是以关键字k本身或关键字加上某个数值常量c作为哈希地址的方法。
- 优点:计算简单,并且不可能有冲突发生
- 缺点:关键字分布不连续将造成内存单元的大量浪费

- 直接定址法是以关键字k本身或关键字加上某个数值常量c作为哈希地址的方法。
-
2. 除留余数法
- 除留余数法是用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址的方法。

- 除留余数法是用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址的方法。
-
3、数字分析法
- 适合于所有关键字值都已知的情况,并需要对关键字中每一位的取值分布情况进行分析。
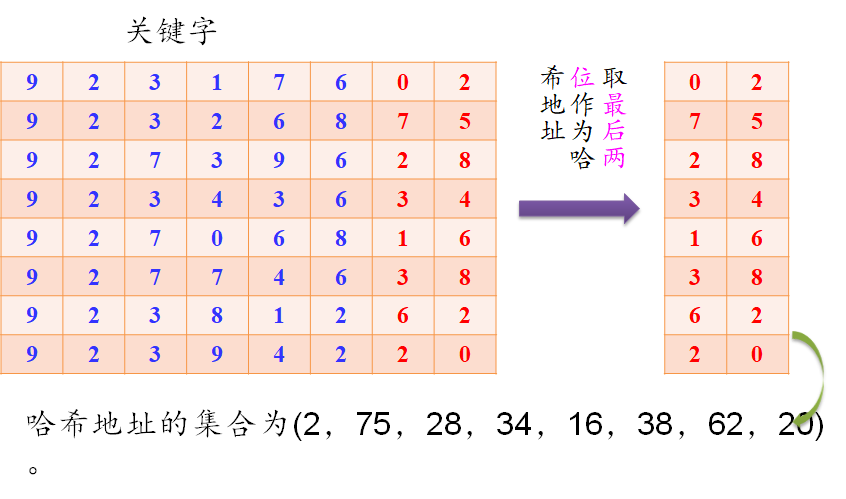
- 适合于所有关键字值都已知的情况,并需要对关键字中每一位的取值分布情况进行分析。
哈希冲突解决方法
-
(1)线性探查法
- 线性探查法的数学递推描述公式为:
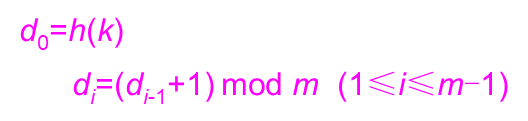
- 线性探查法的数学递推描述公式为:
-
(2)平方探查法
-
平方探查法的数学描述公式为:

-
平方探查法是一种较好的处理冲突的方法,可以避免出现堆积现象。它的缺点是不能探查到哈希表上的所有单元,但至少能探查到一半单元。
-
查找哈希表和哈希链的时间性能ASL
-
对于哈希表:{16,74,60,90,46,17,31,29,88,77}。h=k mod 13
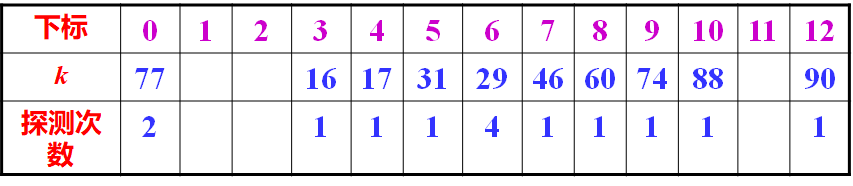
-
1)查找成功ASL:
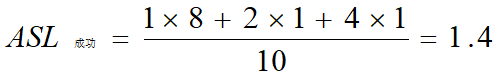
-
2)不成功的ASL:
- 假设查找数为m,计算h(m)
- 查找不成功2种可能:
- 1.h(m)==NULL,探测一次
- 2.h(m)≠NULL,但是m!=key,继续探测,直到 h(key)==NULL
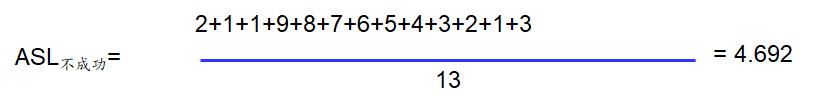
-
总结:
-
查找成功ASL:

-
不成功的ASL:

-
-
-
对于哈希链
-
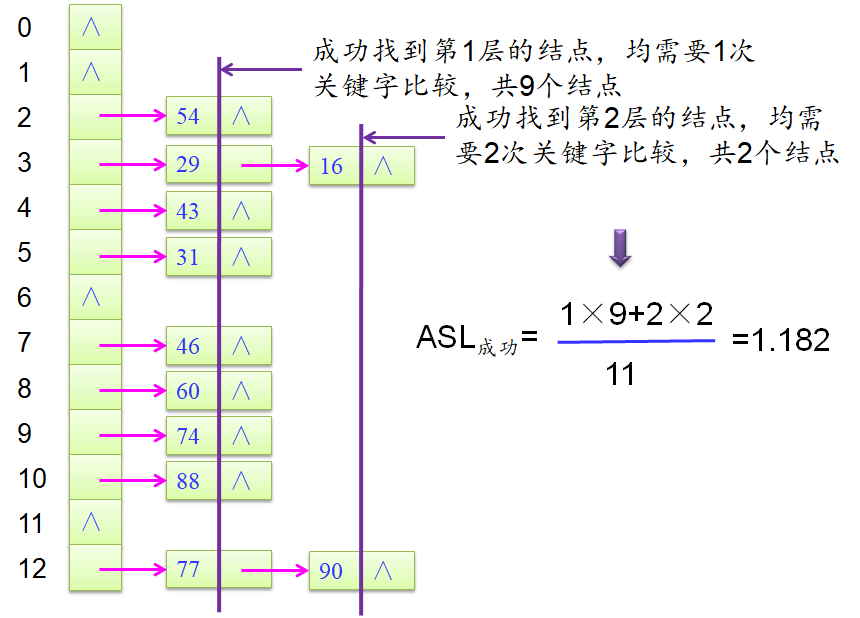
哈希链中成功查找的ASL计算
-
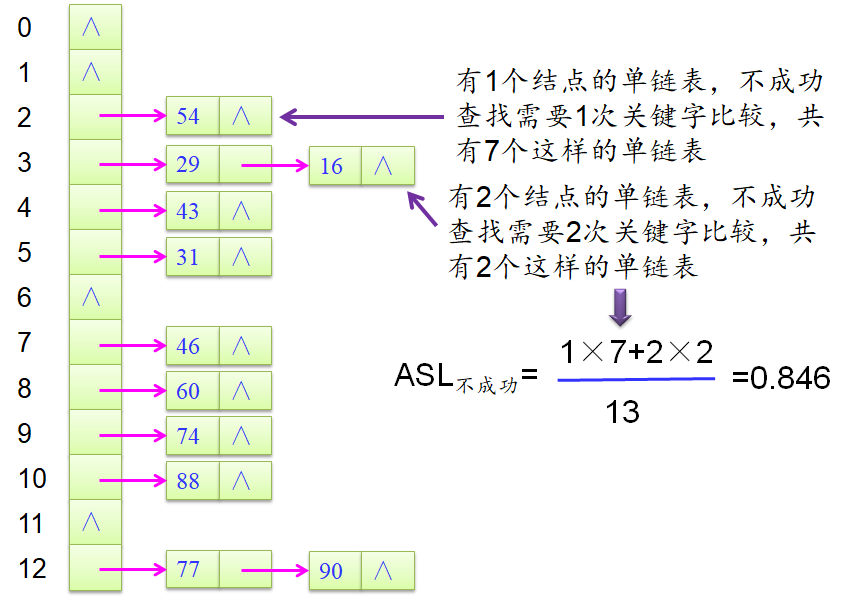
哈希链不成功查找的ASL计算
-
-
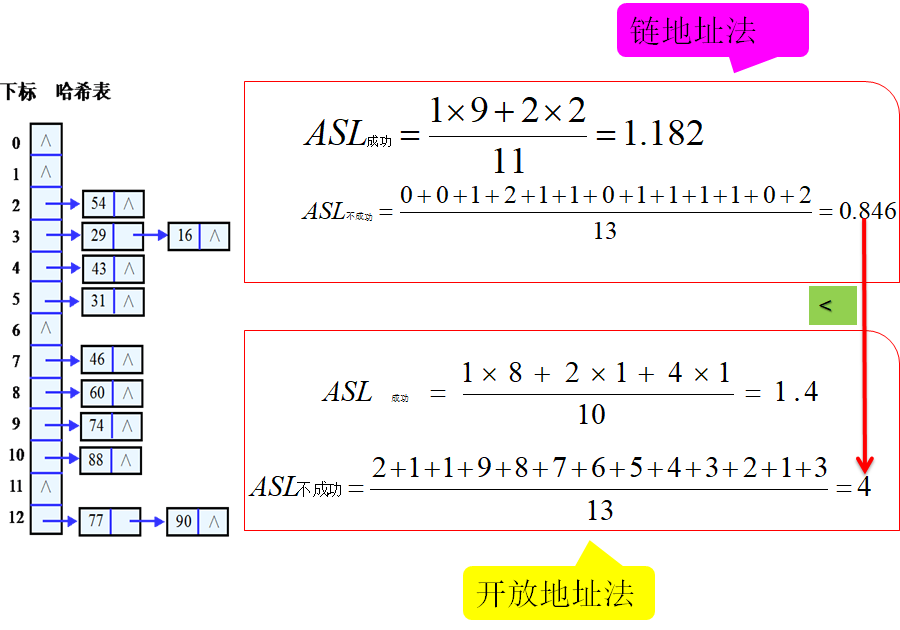
链地址法和开放地址法ASL比较
哈希表上的运算
- 哈希表结构体:
#define MaxSize 100
#define NULLKEY -1
#define DELKEY -2
typedef char *InfoType;
typedef struct
{
int key; // 关键字域
InfoType data; //其他数据域
int count; //探查次数
}HashTable[MaxSize];
- 哈希表插入及建表代码实现
- 每个关键字插入HashTable ha过程
int InsertHT(HashTable ha,int p,int k,int &n)
{ //伪代码
计算k的哈希地址adr=k%p;
若ha[adr]=k,则已存在k,不需要插入
while(ha[adr]不为空 或ha[adr]不等删除标记 )
{
线性探查k的位置。即adr=adr+1;
计算探查次数count
}
ha[adr]=k;
哈希表长度增1
}
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p)
{ //代码实现
int i;
for (i = 0;i < m;i++) //初始化
{
ha[i].key = NULLKEY;
ha[i].count = 0;
ha[i].data = NULL;
}
for (i = 0;i < n;i++) //插入关键字
InsertHT(ha, n, x[i], p);
}
int InsertHT(HashTable ha,int p,int k,int &n)
{
int adr,i;
adr=k % p;
if(adr==NULLKEY || adr==DELKEY) //地址为空,可插入数据
{
ha[adr].key=k;
ha[adr].count=1;
}
else
{
i=1;
while(ha[adr].key!=NULLKEY && ha[adr].key!=DELKEY)
{
adr=(adr+1) % m;
i++;
} //查找插入位置
ha[adr].key=k;ha[adr].count=i; //找到插入位置
}
n++;
}
- 哈希表查找算法
int SearchHT(HashTable ha,int p,int k)
{
int i=0,adr;
adr=k % p;
while(ha[adr].key!=NULLKEY && ha[adr].key!=k)
adr=(adr+1) % m;//探查下一个地址
if(ha[adr].key==NULLKEY) return -1;//地址为空,找不到
if(ha[adr].key==k) return adr; //找到关键字k
else return -1;
}
- 哈希表删除算法
- 查找删除元素,找到话,不能真正删除,做个删除标记DELKEY。
int DeleteHT(HashTable ha,int p,int k,int &n)
{
int adr;
adr=SearchHT(ha,p,k);
if(adr!=-1)
{
ha[adr].key=DELKEY; //逻辑删除,该元素贴删除标记
n--;
return 1;
}
else return 0;
}
哈希链上的运算
-
拉链法是把所有的同义词用单链表链接起来的方法。
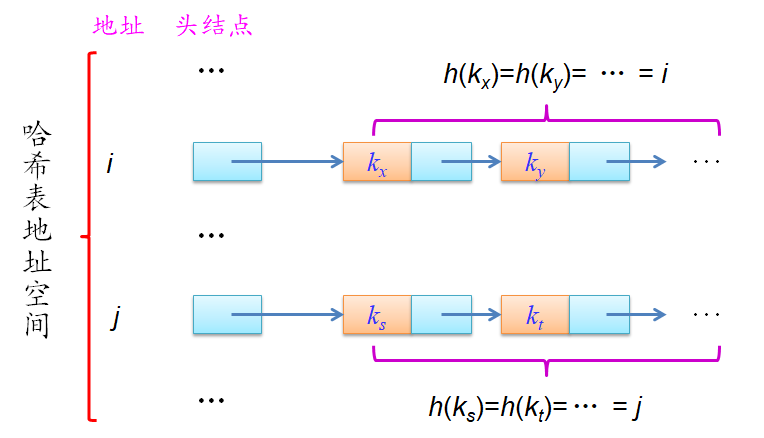
-
哈希链结构体
#define HashSize 20000
#define ID_LAST 17
#define MAXSIZE 20
typedef struct HashNode
{
string ID;
int flight_distance;
struct HashNode* next;
}HashNode, * HashChain;
- 创建哈希链以及插入数据
void CreateHashChain(HashChain HC[], int n, int k)
{
int i;
for (i = 0;i < HashSize;i++)
{
HC[i] = new HashNode;
HC[i]->next = NULL;
}
for (i = 0;i < n;i++) Insert(HC, k);
}
void Insert(HashChain HC[], int k)
{
string ID;
int distance;
int index;
HashChain node;
HashChain p;
ID.resize(MAXSIZE);
scanf("%s%d", &ID[0], &distance);
if (distance < k) distance = k;
index = GetID(ID) % HashSize;
p = HC[index]->next;
while (p != NULL)
{
if (p->ID == ID) break;
else p = p->next;
}
if (p == NULL)
{
node = new HashNode;
node->ID = ID;
node->flight_distance = distance;
node->next = HC[index]->next;
HC[index]->next = node;
}
else p->flight_distance += distance;
}
- 哈希链查找
void Search(HashChain HC[], string ID)
{
int index;
HashChain p;
index = GetID(ID) % HashSize;
p = HC[index]->next;
while (p != NULL)
{
if (p->ID == ID)
{
printf("%d", p->flight_distance);
return;
}
p = p->next;
}
printf("No Info");
}
1.2.谈谈你对查找的认识及学习体会。
查找就是在一堆数据元素中找到我们所需的数据,它是一个平台上最基础的算法,很大部分决定了该平台的运行效率,因此使用高效的查找算法尤为重要。在本章中学习了静态查找中的顺序查找以及二分查找,二分查找的效率更高,学习了新的数据结构--二叉搜索树,也了解了B树和B+树的一些基本操作,还知道了哈希表,哈希链这种时间复杂度为O(1)的高效数据结构,学习完这一章,才发现原来查找有这么多种方法,感觉学到了很多。
2.PTA题目介绍(0--6分)
2.1 7-2 二叉搜索树的最近公共祖先
2.1.1 该题的设计思路
题面分析
- 输入样例:
6 8
6 3 1 2 5 4 8 7
2 5
8 7
1 9
12 -3
0 8
99 99
- 由于
待查询的结点对数 M(≤ 1 000)和二叉搜索树中结点个数 N(≤ 10 000)和最后 M 行,每行给出一对整数键值 U 和 V。所有键值都在整型int范围内都在整型int范围内,所以我们可以用int来存储这些数据。对第二行的先序遍历序列int型数组来存储。
解法
- 1.首先我们需要建树,我们将先序遍历序列升序排序,得到中序遍历序列,然后根据先中序列建树
- 2.然后我们需要在二叉搜索树中寻找所给定的一对键值,并根据相应的情况输出相应的结果
- 3.若这对键值均在树上,则用二分法寻找它们的LCA
代码的时空复杂度
- 时间复杂度:O(MlogN)
- 空间复杂度:O(n)
2.1.2 该题的代码实现
伪代码
BSTree CreateBSTree(int* pre, int* in, int n)
if 没有节点 返回NULL
新建节点bst赋值为根节点
for pos=in to in+n
if 找到根节点 then 退出循环
end for
k=中序序列的逻辑位置
bst->lchid = CreateBSTree(pre + 1, in, k);
bst->rchid = CreateBSTree(pre + k + 1, pos + 1, n - k - 1);
返回bst
BSTree Find(BSTree bst, int key)
while bst不为空
if key小于bst->key then bst移向左子树
else if key大于bst->key then bst移向右子树
else(找到key) 返回bst
end if
end while
查找失败,返回空节点
BSTree SearchLCA(BSTree bst, int u, int v)
while bst不为空
if u和v都在左子树 then bst移向左子树
else if u和v都在右子树 then bst移向右子树
else(u和v在根节点两边或者其中一个为根节点)then 返回LCA
end if
end while
源代码
#include<iostream>
#include<algorithm>
using namespace std;
typedef struct node
{
int key;
struct node* lchid;
struct node* rchid;
}BSTNode, * BSTree;
BSTree SearchLCA(BSTree bst, int u, int v);
BSTree Find(BSTree bst, int key);
BSTree Insert(BSTree bst, int key);
BSTree CreateBSTree(int* pre, int* in, int n);
int main()
{
int m, n;
int i;
int* pre;
int* in;
int u, v;
BSTree bst;
BSTree u_node;
BSTree v_node;
BSTree LCA;
bst = NULL;
cin >> m >> n;
pre = new int[n];
in = new int[n];
for (i = 0;i < n;i++)
{
cin >> pre[i];
in[i] = pre[i];
}
sort(in, in + n);
bst = CreateBSTree(pre, in, n);
for (i = 0;i < m;i++)
{
cin >> u >> v;
u_node = Find(bst, u);
v_node = Find(bst, v);
if (u_node == NULL && v_node == NULL) cout << "ERROR: " << u << " and " << v << " are not found.";
else if (u_node == NULL) cout << "ERROR: " << u << " is not found.";
else if (v_node == NULL) cout << "ERROR: " << v << " is not found.";
else
{
LCA = SearchLCA(bst, u, v);
if (LCA->key == u) cout << u << " is an ancestor of " << v << ".";
else if (LCA->key == v) cout << v << " is an ancestor of " << u << ".";
else cout << "LCA of " << u << " and " << v << " is " << LCA->key << ".";
}
cout << endl;
}
return 0;
}
BSTree SearchLCA(BSTree bst, int u, int v)
{
while (bst != NULL)
{
if (u < bst->key && v < bst->key) bst = bst->lchid;
else if (u > bst->key&& v > bst->key) bst = bst->rchid;
else return bst;
}
return NULL;
}
BSTree Find(BSTree bst, int key)
{
while (bst != NULL)
{
if (key < bst->key) bst = bst->lchid;
else if (key > bst->key) bst = bst->rchid;
else return bst;
}
return NULL;
}
BSTree Insert(BSTree bst, int key)
{
if (bst == NULL)
{
bst = new BSTNode;
bst->key = key;
bst->lchid = bst->rchid = NULL;
}
else if (key < bst->key) bst->lchid = Insert(bst->lchid, key);
else if (key > bst->key) bst->rchid = Insert(bst->rchid, key);
return bst;
}
BSTree CreateBSTree(int* pre, int* in, int n)
{
if (n <= 0) return NULL;
BSTree bst;
int* pos;
int k;
bst = new BSTNode;
bst->key = pre[0];
for (pos = in;pos < in + n;pos++)
{
if (*pos == *pre) break;
}
k = pos - in;
bst->lchid = CreateBSTree(pre + 1, in, k);
bst->rchid = CreateBSTree(pre + k + 1, pos + 1, n - k - 1);
return bst;
}
2.1.3 PTA提交列表
提交列表截图
代码编写中碰到问题及解决方法
-
Q1:建树函数写错了,直接按照先序遍历序列依次顺序建树,导致树过高
-
A1:根据先序遍历序列得到中序遍历序列,然后根据先中序列建树
-
Q2:先是在寻找LCA的过程中从其中一个节点开始,逐渐往上寻找以该节点为根节点的树中是否含有另外一个节点;后来思路是先求出两个节点的高度,然后较高的那个节点上移至与较低的节点同一层,然后一起上移,直至相遇,相遇点就是LCA。两种算法过于复杂,导致运行超时。
-
A2:使用二分法,从根节点开始向下寻找,直至其中一个节点为根节点或者两个节点分别分布在左右子树。
2.1.4 本题设计的知识点
- 1.温习了一遍根据先序和中序序列建树,根据先序创建节点,根据中序划分左右子树
- 2.学习使用二分法,一直靠近所求节点,直至两个节点分叉
- 3.温习了二叉搜索树寻找节点的做法,小于就移向左子树,大于就移向右子树,等于那就是找到了节点
2.2 7-4 整型关键字的散列映射
2.2.1 该题的设计思路
题面分析
- 输入样例
4 5
24 15 61 88
- 由于
两个正整数N(≤1000)和P(≥N的最小素数),分别为待插入的关键字总数、以及散列表的长度以及输入第二行均为整型数据,因而均可以用int存储。
解法
- 建立哈希表,在插入数据的过程中,将插入位置作为Insert函数的返回值,进而输出其逻辑位置
代码的时空复杂度
- 时间复杂度:O(n²)
- 空间复杂度:O(n)
2.2.2 该题的代码实现
伪代码
void CreateHT(HashTable*& ha, int n, int p)
创建并初始化哈希表
for i=0 to n
将数据插入InsertHT(ha, key, p)到哈希表中
输出插入数据的逻辑位置
end for
int InsertHT(HashTable* ha, KeyType k, int p)
adr=计算所得的哈希地址
if ha[adr].key == NULLKEY || ha[adr].key == DELKEY then 插入数据
else
while ha[adr].key != NULLKEY && ha[adr].key != DELKEY
if 发现重复关键字 then 返回所在位置adr
线性探测插入位置
end while
插入数据
end for
返回插入位置adr
源代码
#include<iostream>
#include<limits.h>
#define MaxSize 1010 //定义最大哈希表长度
#define NULLKEY -1 //定义空关键字值
#define DELKEY -2 //定义被删关键字值
using namespace std;
typedef int KeyType; //关键字类型
typedef char* InfoType; //其他数据类型
typedef struct node
{
KeyType key; //关键字域
InfoType data; //其他数据域
int count; //探查次数域
} HashTable; //哈希表类型
int InsertHT(HashTable* ha, KeyType k, int p);
void CreateHT(HashTable*& ha, int n, int p);
int main()
{
int n, p;
HashTable* ha;
cin >> n >> p;
CreateHT(ha, n, p);
return 0;
}
int InsertHT(HashTable* ha, KeyType k, int p)
{
int adr, times;
adr = k % p;
times = 1;
if (ha[adr].key == NULLKEY || ha[adr].key == DELKEY)
{
ha[adr].key = k;
ha[adr].count = times;
}
else
{
while (ha[adr].key != NULLKEY && ha[adr].key != DELKEY)
{
if (k == ha[adr].key) return adr;
adr = (adr + 1) % p;
times++;
}
ha[adr].key = k;
ha[adr].count = times;
}
return adr;
}
void CreateHT(HashTable*& ha, int n, int p)
{
int i;
int key;
int adr;
bool flag;
bool* engaged;
flag = true;
ha = new HashTable[p];
for (i = 0;i < p;i++)
{
ha[i].key = NULLKEY;
ha[i].count = 0;
ha[i].data = NULL;
}
for (i = 0;i < n;i++)
{
cin >> key;
adr = InsertHT(ha, key, p);
if (flag)
{
cout << adr;
flag = false;
}
else cout << ' ' << adr;
}
}
2.2.3 PTA提交列表
提交列表截图

代码编写中碰到问题及解决方法
-
Q1:重复关键字重复插入到哈希表中
-
A1:若发现重复的关键字就return
-
Q2:发现重复的关键字,return -1,题意没有理解清楚
-
A2:修正为return原来的插入位置
2.2.4 本题设计的知识点
- 1.练习哈希表的建立,每次插入一个关键字,出现哈希冲突就使用线性探测的方法解决冲突
- 2.在插入关键字之前要先进行初始化,不然会因为自动给定的初始值不是NULLKEY导致无法插入
2.3 7-5(哈希链) 航空公司VIP客户查询
2.3.1 该题的设计思路
题面分析
- 输入样例
4 500
330106199010080419 499
110108198403100012 15000
120104195510156021 800
330106199010080419 1
4
120104195510156021
110108198403100012
330106199010080419
33010619901008041x
- 由于
正整数N(≤10⁵)和K(≤500)和正整数M(≤10⁵)均在整型范围内,因而可用int来存储;对于身份证可用stl库中的string类来存储,而飞行里程也可以使用int型来存储数据
解法
- 首先是要建立起顾客信息的哈希链
- 根据客户的ID,取后五位转化为数字,然后计算哈希地址
- 遍历对应的链,如果已存在相同的ID,则直接累加里程即可,不存在则添加
- 对应每个需要查询的信息,同样的方法取哈希地址,之后遍历查找即可
代码的时空复杂度
- 时间复杂度:O(n²)
- 空间复杂度:O(n)
2.3.2 该题的代码实现
伪代码
void CreateHashChain(HashChain HC[], int n, int k)
初始化哈希链hc
for i=0 to n
Insert(HC, k)插入关键字
end for
void Insert(HashChain HC[], int k)
输入ID和飞行里程
数据处理并计算哈希地址
while 遍历对应的单链表
if 查找到对应的ID then break
else p = p->next
end while
if 没查找到
申请节点并复制
头插法插入关键字
else
累加飞行里程
end for
void Search(HashChain HC[], string ID)
计算哈希地址
while 遍历哈希地址对应的单链表
if 找到 then 输出总飞行里程
else p = p->next
end while
未找到,输出No Info
源代码
#include<iostream>
#define HashSize 20000
#define ID_LAST 17
#define MAXSIZE 20
using namespace std;
typedef struct HashNode
{
string ID;
int flight_distance;
struct HashNode* next;
}HashNode, * HashChain;
void CreateHashChain(HashChain HC[], int n, int k);
void Insert(HashChain HC[], int k);
int GetID(string ID);
void Search(HashChain HC[], string ID);
int main()
{
int n, k, m;
int i;
string ID;
HashChain* HC;
HC = new HashChain[HashSize];
ID.resize(MAXSIZE);
scanf("%d%d", &n, &k);
CreateHashChain(HC, n, k);
scanf("%d", &m);
for (i = 0;i < m;i++)
{
scanf("%s", &ID[0]);
Search(HC, ID);
printf("\n");
}
return 0;
}
void Search(HashChain HC[], string ID)
{
int index;
HashChain p;
index = GetID(ID) % HashSize;
p = HC[index]->next;
while (p != NULL)
{
if (p->ID == ID)
{
printf("%d", p->flight_distance);
return;
}
p = p->next;
}
printf("No Info");
}
void CreateHashChain(HashChain HC[], int n, int k)
{
int i;
for (i = 0;i < HashSize;i++)
{
HC[i] = new HashNode;
HC[i]->next = NULL;
}
for (i = 0;i < n;i++) Insert(HC, k);
}
void Insert(HashChain HC[], int k)
{
string ID;
int distance;
int index;
HashChain node;
HashChain p;
ID.resize(MAXSIZE);
scanf("%s%d", &ID[0], &distance);
if (distance < k) distance = k;
index = GetID(ID) % HashSize;
p = HC[index]->next;
while (p != NULL)
{
if (p->ID == ID) break;
else p = p->next;
}
if (p == NULL)
{
node = new HashNode;
node->ID = ID;
node->flight_distance = distance;
node->next = HC[index]->next;
HC[index]->next = node;
}
else p->flight_distance += distance;
}
int GetID(string ID)
{
int last_5_ID = 0;
int i;
for (i = 12;i < ID_LAST;i++)
last_5_ID = last_5_ID * 10 + (ID[i] - '0');
if (ID[ID_LAST] == 'x') last_5_ID = last_5_ID * 10 + 10;
else last_5_ID = last_5_ID * 10 + (ID[i] - '0');
return last_5_ID;
}
2.3.3 PTA提交列表
提交列表截图

代码编写中碰到问题及解决方法
-
Q1:直接取ID的最后一位作为哈希地址,导致每条单链表过长
-
A1:取后五位的对哈希表长度进行取余,余数作为哈希地址,扩大哈希表长度,以减少每条单链表的长度
-
Q2:使用cin和cout耗时过长,导致运行超时
-
A2:改用scanf和pritf进行输入输出
2.3.4 本题设计的知识点
- 1.练习哈希链的创建和查找,创建就是计算哈希地址,然后插入对应的单链表中;查找也得先计算哈希地址,然后在单链表中查找对应的信息
- 2.使用cin和cout比起使用scanf和pritf来输入输出,要更加耗时,在时间限制严格的题目中,应该使用scanf和pritf来输入输出
- 3.创建哈希链的过程中,应该注意不要让单链表的长度过长,否则查找和插入都将耗时过长
- 4.使用scanf来对string进行输入时,应先使用resize方法重新申请空间,因为默认申请的空间可能不足以容纳数据,比如该题的ID;同时语句的格式也应该注意,应该使用
scanf("%s", &ID[0]);,而非scanf("%s", ID);,后者的格式无法输入




