DS博客作业02--栈和队列
0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
栈
- 栈的基本认识
栈(stack):栈是限定仅在表的一端进行插入或删除操作的线性表。
我们把允许插入和删除操作的一端称为栈顶(top),另一端称为栈底(bottom)。不含任何数据元素的栈称为空栈。栈又称为“后进先出(Last In First Out,简称LIFO)的线性表”,简称为LIFO结构。
栈的插入操作,称为进栈/入栈/压栈。
栈的删除操作,称为出栈/弹栈。
不过要注意的是,最先进栈的元素不代表最后出栈。栈对线性表的插入删除位置做了限制,但并没有对出栈和入栈的时间做限制。也就是说,在不是所有元素都入栈的情况下,事先入栈的元素也可以在任意时间出栈,只要保证每次出栈的元素都是栈顶元素就可以。 - 栈的顺序存储结构
顺序栈是栈的顺序实现。顺序栈是指利用顺序存储结构实现的栈。采用地址连续的存储空间(数组)依次存储栈中数据元素,由于人栈和出栈运算都是在栈顶进行,而栈底位置是固定不变的,可以将栈底位置设置在数组空间的起始处;栈顶位置是随入栈和出栈操作而变化的,故需用一个整型变量top来记录当前栈顶元素在数组中的位置
顺序栈的结构定义:
typedef int SElemType;
typedef int Status;
struct SqStack
{
SElemType *base;
SElemType *top;
int stacksize;
};
- 顺序栈的操作
1.栈的初始化
Status InitStack(SqStack &S)
{
S.base = (SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));
if(!S.base) return OVERFLOW;
S.top = S.base;
S.stacksize = STACK_INIT_SIZE;
return OK;
}
2.销毁栈
Status DestoryStack(SqStack &S)
{
free(S.base);
S.base = NULL;
S.top = NULL;
S.stacksize = 0;
return OK;
}
3.清空栈
Status ClearStack(SqStack &S)
{
S.top = S.base;
return OK;
}
4.判断栈空
Status StackEmpty(SqStack S)
{
if(S.top == S.base)
return TRUE;
else
return FALSE;
}
5.取栈长
int StackLength(SqStack S)
{
return S.top - S.base;
}
6.取栈顶
Status GetTop(SqStack S,SElemType &e)
{
if(S.top == S.base) return ERROR;
e = *(S.top -1);
return OK;
}
7.入栈
Status Push(SqStack &S, SElemType e)
{
if(S.top - S.base >= S.stacksize)
{
S.base = (SElemType *)realloc(S.base,(S.stacksize + STACKINCREMENT)*sizeof(SElemType));
if(!S.base) return OVERFLOW;
S.top = S.base + S.stacksize;
S.stacksize += STACKINCREMENT;
}
*S.top++ = e;
return OK;
}
8.出栈
Status Pop(SqStack &S, SElemType &e)
{
if(S.top == S.base) return ERROR;
e = * --S.top;
return OK;
}
- 栈的链式存储结构
对于顺序栈来说,主要的缺点就是栈的大小已经固定,若有超过栈长的元素个数,则此时栈会发生“溢出”。这时我们可以采用链式栈的存储结构,这样就不用再考虑栈的空间是否足够大的问题。
栈的链式存储结构,简称为链栈。
思考:对于栈的链式存储结构来说,栈顶指针是在链表头结点位置更好,还是在链表尾节点位置更好?
答:头结点位置更好
链表有头指针,而栈的主要操作也是在栈顶进行,那么我们就可以将二者合一,将单链表的头指针作为栈顶指针,即栈的链式存储结构的栈顶指针为单链表的头指针。
链栈的结构定义:
typedef char ElemType;
typedef struct linknode
{
ElemType data;
struct linknode *next;
}LinkStNode;LinkStNode *s;
- 链栈的操作
1.初始化栈
void InitStack(LinkStNode*&s)//初始化栈
{
cout<<"初始化栈"<<endl;
s=(LinkStNode*)malloc(sizeof(LinkStNode));
s->next=NULL;
}
2.进栈
void Push(LinkStNode*&s)//进栈
{
ElemType e;
int i=0;
LinkStNode *p;
cout<<"依次进栈的元素为:";
while (i<n)
{
cin>>e;
p=(LinkStNode*)malloc(sizeof(LinkStNode));
p->data=e;
p->next=s->next;
s->next=p;
i++;
}
}
3.判断栈空
void StackEmpty(LinkStNode *s)//判断栈是否为空
{
if(s->next==NULL)
{
cout<<"栈为空"<<endl;
}
else
cout<<"栈非空"<<endl;
}
4.取栈顶
void GetTop(LinkStNode*s)//得到栈顶元素
{
if(s->next!=NULL)
{
cout<<"栈顶元素为:";
cout<<s->next->data;
cout<<endl;
}
}
5.出栈
void Pop(LinkStNode *&s)//出栈操作
{
cout<<"出栈序列为:";
LinkStNode *p;
while(s->next!=NULL)
{
cout<<s->next->data<<" ";
p=s->next;
s->next=p->next;
free(p);
}
cout<<endl;
}
6.销毁栈
void DestroyStack(LinkStNode*&s)//释放栈
{
cout<<"释放栈";
LinkStNode *q=s,*p=s->next;
while(p!=NULL)
{
free(q);
q=p;
p=q->next;
}
free(q);
}
- 栈的应用:后缀表达式
对于数学运算来说,确定运算符的优先级是十分重要的,直接决定了该算式是否计算正确。在实际生活中,我们书写的算式都是中缀表达式,即运算符(此处特指算数运算符)在操作数中间。例如:
9+(3-1)*3+10/2
我们把这种平时使用的四则运算表达式的写法称为中缀表达式。但是对于计算机而言,中缀表达式并不方便。计算机计算都是从左到右顺序计算,在该算式中,*在+之后,但是却要先于+进行运算,而加入括号后,运算则会变得更加复杂。
对于四则运算,20世纪50年代,波兰逻辑学家Jan Lukasiewicz发明了一种不需要括号的表达式方法,称为后缀表示法,也称为逆波兰(Reverse Polish Notation,简称RPN)表示法。
那么,如何把中缀表达式转化为后缀表达式呢?方法:
从左至右遍历中缀表达式的每个数字和符号,按照以下规则,直到最终输出后缀表达式:
使用map容器将-+和1配对,*/和2配对,(和3配对
for 遍历字符串
if 遇到) then 一直出栈至遇到(为止
else if 遇到数字或者小数点 then 直接出栈
else if 遇到(+ || -)&&(在第一位 || 前面不是数字不是) ) (为正负号) then
直接出栈
else if 遇到运算符 then
while 栈不空
if 运算符优先级大于栈顶优先级 或 栈顶为(
直接入栈
否则 出栈
end if
end while
if 栈空 then 运算符入栈
end if
遍历完字符串后 if 栈不空 then
一直出栈至栈空
end if
我们以下面的算式为例进行讲解
9+(3-1)*3+10/2------>9 3 1 - 3 * + 10 2 / +
1.初始化一个空栈,用于对符号进出栈使用。
2.第一个数字是9,输出9。后面的符号+入栈。
3.第三个字符是(,依然是符号,因其是左括号还未配对,故进栈。
4.第四个字符是数字3,输出,此时表达式为9 3,接着符号-进栈。
5.接下来是数字1,输出,此时表达式为9 3 1,后面是符号),此时我们需要把(之前的所有元素都出栈,直至输出(为止。此时总的表达式是9 3 1 -。
6.紧接着是符号,因为此时的栈顶符号是+,优先级低于,因此不输出,进栈。紧接着是数字3,输出,总表达式为9 3 1 – 3.
7.之后是符号+,此时栈顶元素是,比+优先级高,因此栈中元素出栈并输出(因为没有比+更低优先级的符号,所以全部出栈),总输出表达式为9 3 1 – 3 * +。然后将这个符号+进栈。
8.紧接着输出数字10,总表达式为9 3 1 – 3 * + 10。之后是符号/,所以/进栈。
9.最后一个数字为2,此时总表达式为9 3 1 – 3 * + 10 2。
10.因已到最后,所以将栈中符号全部出栈。最终获得的后缀表达式为9 3 1 – 3 * + 10 2 / +。
具体的代码实现如下:
#include<iostream>
#include<map>
#include<stack>
#include<string>
using namespace std;
void InfixToSuffix(string infix, string& suffix);
int main()
{
string infix;
string suffix;
cin >> infix;
InfixToSuffix(infix, suffix);
cout << suffix;
return 0;
}
void InfixToSuffix(string infix, string& suffix)
{
int i;
int len;
map<char,int> op;
stack<char> oper;
len = infix.length();
op['-'] = 1;op['+'] = 1;op['*'] = 2;op['/'] = 2;op['('] = 3;
for (i = 0;i <= len;i++)
{
if (infix[i] == ')')
{
while (oper.top() != '(')
{
suffix = suffix + oper.top() + ' ';
oper.pop();
}
oper.pop();
}
else if (isdigit(infix[i])||infix[i]=='.')
{
while (isdigit(infix[i]) || infix[i] == '.')
{
suffix += infix[i];
i++;
}
suffix += ' ';
i--;
}
else if ((infix[i] == '-' || infix[i] == '+') && (i == 0 || (infix[i - 1] != ')' && !isdigit(infix[i - 1]))))
{
if (infix[i] == '-')
{
suffix += infix[i];
}
}
else
{
while (!oper.empty())
{
if (op[infix[i]] > op[oper.top()] || oper.top() == '(')
{
oper.push(infix[i]);
break;
}
else
{
suffix = suffix + oper.top() + ' ';
oper.pop();
}
}
if (oper.empty())
{
oper.push(infix[i]);
}
}
}
while (!oper.empty())
{
suffix = suffix + oper.top() + ' ';
oper.pop();
}
suffix.erase(suffix.length() - 3);
}
队列
- 队列的基本认识
队列(queue):队列是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入操作的一端称为队尾,允许删除操作的一端称为队头。
队列与现实生活中的排队机制很像,排在队头的出队,而想入队则只能从队尾开始。
队列的基本操作包括:
初始化队列:InitQueue(Q)
操作前提:Q为未初始化的队列。
操作结果:将Q初始化为一个空队列。
判断队列是否为空:IsEmpty(Q)
操作前提:队列Q已经存在。
操作结果:若队列为空则返回1,否则返回0。
判断队列是否已满:IsFull(Q)
操作前提:队列Q已经存在。
操作结果:若队列为满则返回1,否则返回0。
入队操作:EnterQueue(Q,data)
操作前提:队列Q已经存在。
操作结果:在队列Q的队尾插入data。
出队操作:DeleteQueue(Q,&data)
操作前提:队列Q已经存在且非空。
操作结果:将队列Q的队头元素出队,并使用data带回出队元素的值。
取队首元素:GetHead(Q,&data)
操作前提:队列Q已经存在且非空。
操作结果:若队列为空则返回1,否则返回0。
清空队列:ClearQueue(&Q)
操作前提:队列Q已经存在。
操作结果:将Q置为空队列。
- 队列的顺序存储结构之循环队列
队列的顺序存储有很大的缺陷,会造成大量的已出队的元素的存储空间浪费。而且,若此时入队元素已经大于n,则我们需要更大的存储空间才行,但队头位置有大量空间未利用,空间浪费严重。
解决以上问题的方法就是如果后面满了,则我们就从头开始,也就是将队列做成头尾相接的循环。我们把这种头尾相接的顺序存储结构的队列称为循环队列。
循环队列的结构定义:
typedef int DataType; //队列中元素类型
typedef struct Queue
{
DataType Queue[MaxSize];
int fornt; //队头指针
int rear; //队尾指针
}SeqQueue;
- 循环队列的基本操作
1.初始化队列:InitQueue(Q)
//队列初始化,将队列初始化为空队列
void InitQueue(SeqQueue *SQ)
{
SQ->fornt = SQ->rear = 0; //把对头和队尾指针同时置0
}
2.判断队列是否为空:IsEmpty(Q)
//判断队列为空
int IsEmpty(SeqQueue* SQ)
{
if (SQ->fornt == SQ->rear)
{
return 1;
}
return 0;
}
3.判断队列是否已满:IsFull(Q)
//判断队列是否为满
int IsFull(SeqCirQueue* SCQ)
{
//尾指针+1追上队头指针,标志队列已经满了
if ((SCQ->rear + 1) % MaxSize == SCQ->fornt)
{
return 1;
}
return 0;
}
4.入队操作:EnterQueue(Q,data)
int EnterSeqCirQueue(SeqCirQueue* SCQ, DataType data)
{
if (IsFull(SCQ))
{
printf("队列已满,不能入队!\n");
return 0;
}
SCQ->Queue[SCQ->rear] = data;
SCQ->rear = (SCQ->rear + 1) % MaxSize; //重新设置队尾指针
}
5.出队操作:DeleteQueue(Q,&data)
int DeleteSeqCirQueue(SeqCirQueue* SCQ,DataType* data)
{
if (IsEmpty(SCQ))
{
printf("队列为空!\n");
return 0;
}
*data = SCQ->Queue[SCQ->fornt];
SCQ->fornt = (SCQ->fornt + 1) % MaxSize; //重新设置队头指针
}
6.取队首元素:GetHead(Q,&data)
int GetHead(SeqCirQueue* SCQ,DataType* data)
{
if (IsEmpty(SCQ))
{
printf("队列为空!\n");
return 0;
}
*data = SCQ->Queue[SCQ->fornt];
return *data;
}
7.清空队列:ClearQueue(&Q)
void ClearSeqCirQueue(SeqCirQueue* SCQ)
{
SCQ->fornt = SCQ->rear = 0;
}
- 队列的链式存储结构
队列的链式存储结构简称为链式队列,它是限制仅在表头进行删除操作和表尾进行插入操作的单链表。链队的操作实际上是单链表的操作,只不过是出队在表头进行,入队在表尾进行。入队、出队时分别修改不同的指针。
链式队列的结点是动态开辟的,入队时,为新节点开辟空间,出队使释放出队元素结点的空间。所以相对于顺序队列和循环队列,链式队列没有判断队列是否为满操作。但在清空队列时需要将队列所有结点的空间动态释放,从而防止内存泄露。
链式队列的结构定义:
typedef int DataType;
typedef struct Node
{
DataType _data;
struct Node* _next;
}LinkQueueNode;
typedef struct
{
LinkQueueNode* front;
LinkQueueNode* rear;
}LinkQueue;
- 链式队列的操作
1.初始化队列
//初始化队列
void InitLinkQueue(LinkQueue* LQ)
{
//创建一个头结点
LinkQueueNode* pHead = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(pHead);
LQ->front = LQ->rear = pHead; //队头和队尾指向头结点
LQ->front->_next = NULL;
}
2.判断队列是否为空
//判断队列是否为空
int IsEmpty(LinkQueue* LQ)
{
if (LQ->front->_next == NULL)
{
return 1;
}
return 0;
}
3.入队
//入队操作
void EnterLinkQueue(LinkQueue* LQ, DataType data)
{
//创建一个新结点
LinkQueueNode* pNewNode = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(pNewNode);
pNewNode->_data = data; //将数据元素赋值给结点的数据域
pNewNode->_next = NULL; //将结点的指针域置空
LQ->rear->_next = pNewNode; //将原来队列的队尾指针指向新结点
LQ->rear = pNewNode; //将队尾指针指向新结点
}

4.出队
//出队操作
void DeleteLinkQueue(LinkQueue* LQ,DataType* data)
{
if (IsEmpty(LQ))
{
printf("队列为空!\n");
return;
}
//pDel指向队头元素,由于队头指针front指向头结点,所以pDel指向头结点的下一个结点
LinkQueueNode* pDel = LQ->front->_next;
*data = pDel->_data; //将要出队的元素赋给data
LQ->front->_next = pDel->_next; //使指向头结点的指针指向pDel的下一个结点
//如果队列中只有一个元素,将队列置空
if (LQ->rear = pDel)
{
LQ->rear = LQ->front;
}
free(pDel); //释放pDel指向的空间
}

5.取队头元素
//取队头元素
int GetHead(LinkQueue* LQ, DataType* data)
{
if (IsEmpty(LQ))
{
printf("队列为空!\n");
return 0;
}
LinkQueueNode* pCur;
pCur = LQ->front->_next; //pCur指向队列的第一个元素,即头结点的下一个结点
*data = pCur->_data; //将队头元素值赋给data
return *data; //返回队头元素值
}
6.清空队列
//清空队列
void ClearQueue(LinkQueue* LQ)
{
while (LQ->front != NULL)
{
LQ->rear = LQ->front->_next; //队尾指针指向队头指针的下一个结点
free(LQ->front); //释放队头指针指向的结点
LQ->front = LQ->rear; //队头指针指向队尾指针
}
}
- 队列应用:报数游戏
题干:报数游戏是这样的:有n个人围成一圈,按顺序从1到n编好号。从第一个人开始报数,报到m(m<n)的人退出圈子;下一个人从1开始报数,报到m的人退出圈子。如此下去,直到留下最后一个人。其中n是初始人数;m是游戏规定的退出位次(保证为小于n的正整数)。
分析:使用队列可以很好的模拟报数游戏,如果报数为m那么退出队列,否则重新进入队列,重复此过程直至队列为空,即所有人都退出圈子
解题思路(以伪代码的形式呈现):
输入队列
while 队列中有元素
出队
if 报数为m then 输出该元素
else 入队
end if
end while
具体实现代码如下:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
void CountGame(queue<int> qu, int m, int n);
int main()
{
queue<int> qu;
int n;
int m;
int i;
cin >> n >> m;
for (i = 1;i <= n;i++)
{
qu.push(i);
}
CountGame(qu, m, n);
return 0;
}
void CountGame(queue<int> qu, int m, int n)
{
if (m >= n)
{
cout << "error!";
return;
}
int temp;
int num = 0;
int flag = 1;
while (!qu.empty())
{
temp = qu.front();
qu.pop();
num++;
if (num == m)
{
if (flag)
{
cout << temp;
flag = 0;
}
else cout << " " << temp;
num = 0;
}
else qu.push(temp);
}
}
关于顺序存储和链式存储的选择,总体来说
- 若可以大致确定元素个数的情况下,推荐使用顺序存储
- 若无法事先预知元素个数,则应使用链式存储
1.2.谈谈你对栈和队列的认识及学习体会
- 对栈和队列的认识
栈是限定仅在表尾进行插入和删除操作的线性表,是一种具有后进先出的数据结构,又称为后进先出的线性表,也就是说后存放的先取,先存放的后取,这就类似于我们要在取放在箱子底部的东西(放进去比较早的物体),我们首先要移开压在它上面的物体(放进去比较晚的物体)。
队列是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。和栈一样,队列是一种操作受限制的线性表。队列是一种先进先出的数据结构,又称为先进先出的线性表,也就是说先放的先取,后放的后取,就如同行李过安检的时候,先放进去的行李在另一端总是先出来,后放入的行李会在最后面出来。 - 学习体会
最近学习了栈和队列的知识,从最初的看到就懵逼到现在对它们有一个清晰的认识,并能够进行简单的应用,就说明还是学到了一点东西。栈和队列这两种数据结构可以很轻易地解决某些特定的问题,也难怪老师说选对了数据结构,题目就解决了一半多。好好学习,天天向上!
2.PTA实验作业
2.1 表达式转换
2.1.1 代码截图

2.1.2 本题PTA提交列表说明
-
PTA提交列表

-
说明
| 错误 | 解决办法 |
|---|---|
| 多种错误 | 将运算符栈为空的情况单独考虑,并修正输出格式 |
2.2 符号配对
2.2.1 代码截图
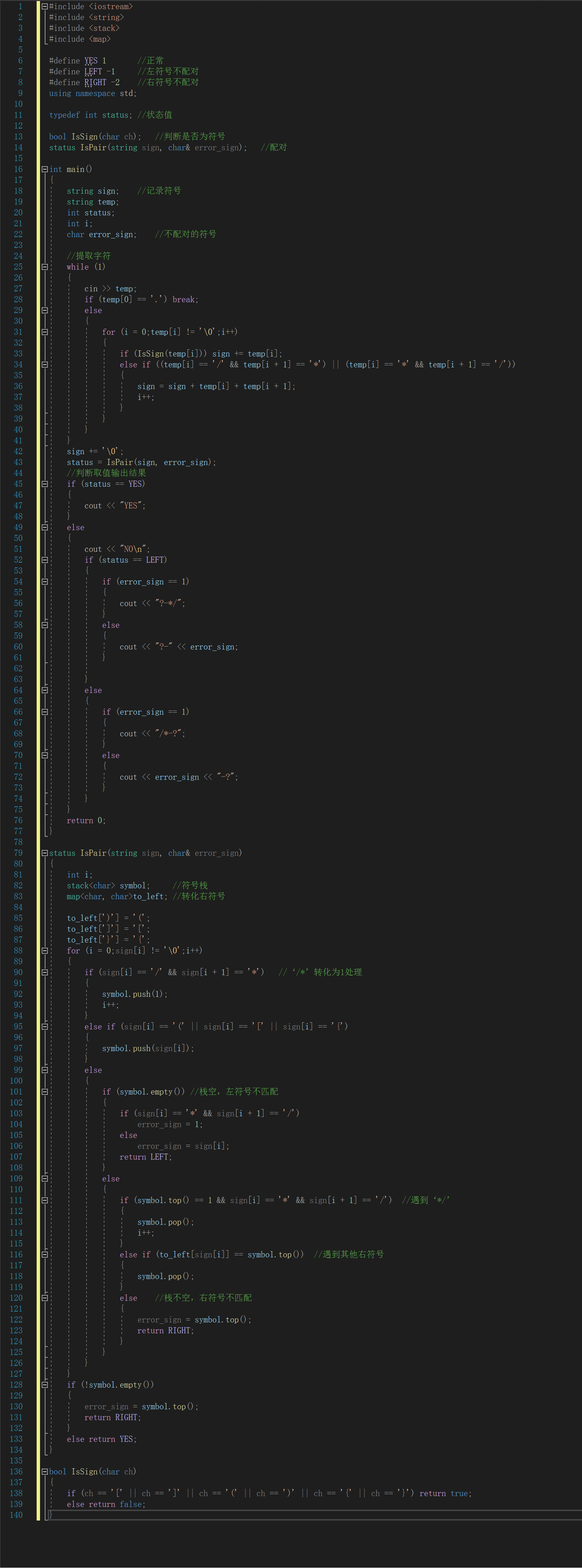
2.2.2 本题PTA提交列表说明
-
PTA提交列表

-
说明
| 错误 | 解决办法 |
|---|---|
| Map容器转化反了 | 将右符号转化成左符号 |
| /*可能是乘除号 | 限制/后是或者后是/才是符号 |
| 开头多余左符号没有判断 | 最后判断栈是否空,空则配对,不空则右符号不匹配 |
3.阅读代码
3.1 题目及解题代码
题干:

题解:

3.1.1 该题的设计思路
设计思路:将数字直接放入栈内,遇到其他字符转化为对应的数字存入栈内,最后将栈内的数字一一取出相加就是得分的总和
时间复杂度:O(n)。需要遍历一次字符数组,遍历一次栈。
空间复杂度:O(n)。分配空间给了int型的index和res,以及一个栈。
3.1.2 该题的伪代码
for 遍历字符串
if 是"C" then 出栈
else
if 是"+" then tmp=栈内头两个数相加
else if 是"D" then tmp=栈顶*2
else tmp=得分
入栈tmp
end if
end if
for 出栈所有元素
累加到res中
end for
返回res
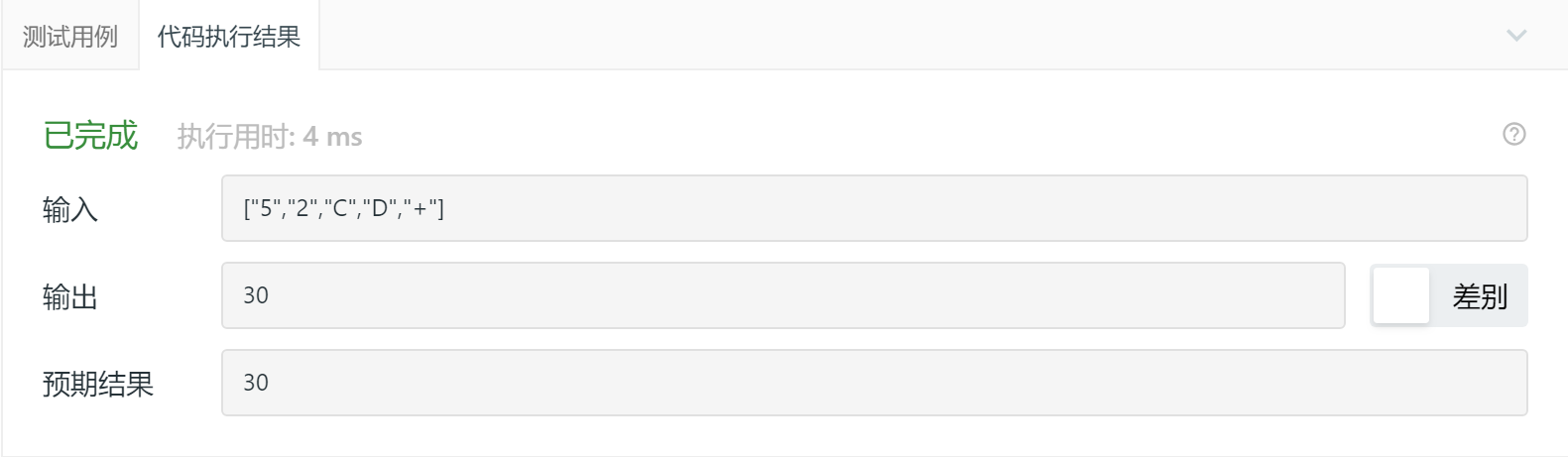
3.1.3 运行结果
3.1.4分析该题目解题优势及难点
-
解题优势
- 使用vector容器,就不用再考虑需要多少空间
- 将对应的操作字符转化为数字,统一了数据类型
- 使用for+auto遍历栈方便快捷
-
难点:
- 如何将操作字符转化为对应的数据
3.2 题目及解题代码
题干:
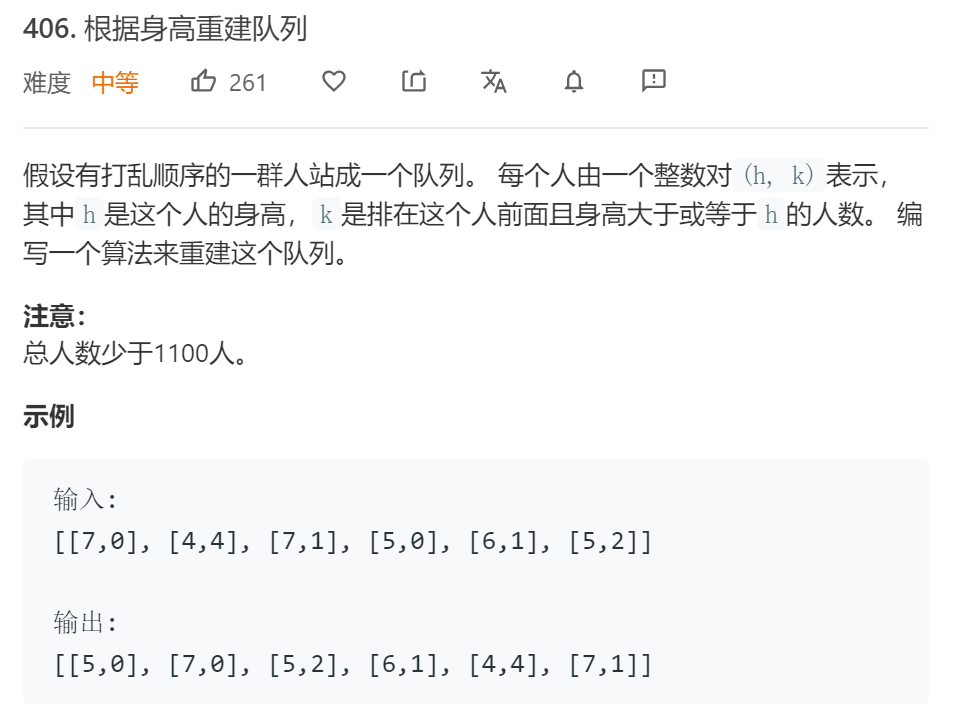
题解:

3.2.1 该题的设计思路
设计思路:
- 先排身高更高的,这是要防止后排入人员影响先排入人员位置
- 每次排入新人员[h,k]时,已处于队列的人身高都>=h,所以新排入位置就是people[k]
时间复杂度:O(n)。sort排序一次,for循环遍历list,重建vector容器
空间复杂度:O(n)。新建list存放people中的数据,重建vector存放排序好的数据
3.2.2 该题的伪代码
将people按照身高降序排序
相同身高需要按k升序排序
新建list容器tmp临时存放people中的数据
for 遍历tmp
寻找并将数据插入对应位置
end for
返回 根据tmp新建的vector容器
3.2.3 运行结果

3.1.4分析该题目解题优势及难点
- 解题优势:
- 使用sort函数,并重载比较函数,很方便的按照所需将数据排序好
- 使用list容器进行插入操作,代码的执行效率更高
- 难点
- 如何在存在k限制的情况下将身高排序好



