Java--算法--基础知识

1. 时间复杂度

   1. 时间复杂复杂度就是程序的循环次数
      分类：O(1),O(logn),O(n),o(nlogn),O(n^2),o(o^3)

      • 常数阶O(1)

      • 对数阶O(logN)

      • 线性阶O(n)

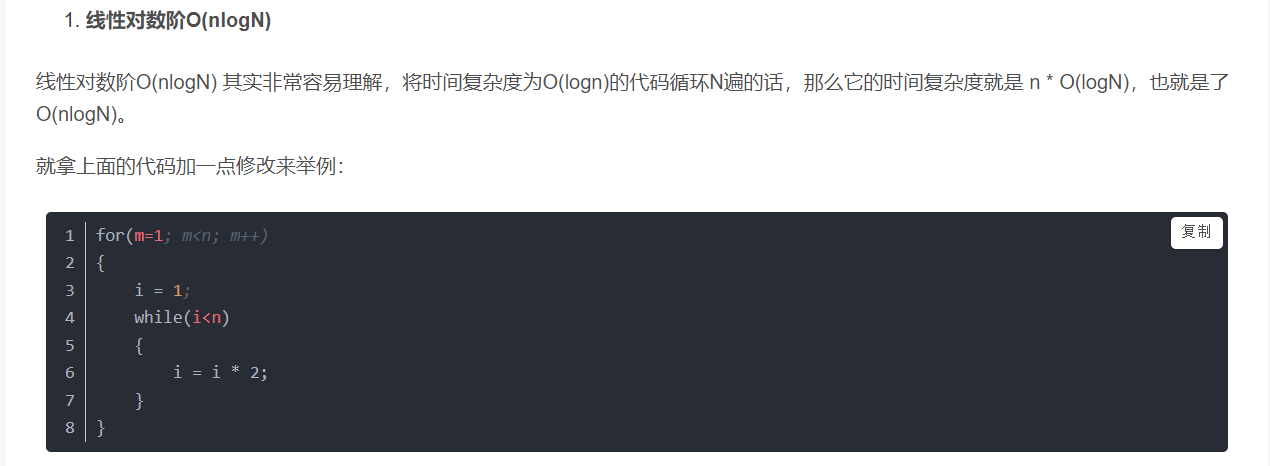
      • 线性对数阶O(nlogN)

      • 平方阶O(n²)

      • 立方阶O(n³)

      • K次方阶O(n^k)【n的k次方，符号不会敲】

      • 指数阶(2^n)

   2. 

   3. 

       

       

   4. 

       

       

   5. 

       

       

   6. 

       

       

   7. 

       

       

       

      　　
2. 空间复杂度:

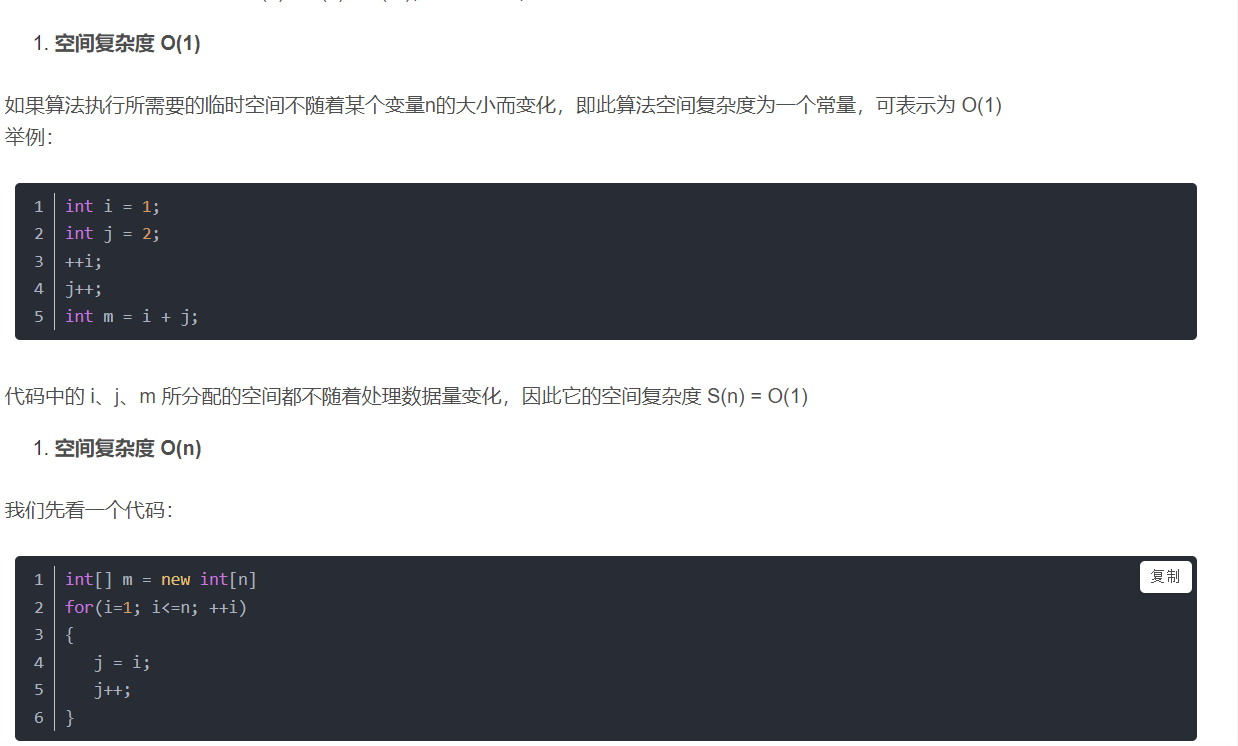
   1. 空间复杂度就是所占用的空间会不会随这程序执行次数的增加而增加
      如果不随程序执行次数增加，就是固定占用空间则空间复杂度但是o(1)
      反之为o(n)

   2.  

3.  ^运算：

   1. 0^n=n
      n^n=0
      满足交换律和结合律
      
      交换a和b两个数：
      a=a^b;
      b=a^b;
      a=a^b;
      
      
      题目：一个数组，已知：某个数出现次数为奇数次，其他的数都出现偶数次，求出这个数
      int res=0;  让res和数组中所有的数都异或一次的最后的结果就是我们要求的出现奇数次的数
      
      题目：一个数组，已知：某两个数出现次数事奇数次，其他的都是偶数次，求出这两个数
      int res=0; 让res和数组中所有的数都进行异或操作的得到的数事 a^b a:出现奇数次的数，b:出现奇数次的数
      res=a^b  res就是一个数，比如说：res=1000 0000， 这就是说明a^b=1000 0000 即a和b在第八位上的数不相等，只有两种情况a的第八位为1,b的第八位为0，或者是a的第八位为0，b的第八位为1
      在定义一个数 int res1=0;让res1异或数组中所有第八位上是 1 的数，即只包含了a或者b中的一个数，最后得到的就是a或者b
      再让 res^res1 的到了 a,b中的另一个数
      结果就是 ：res1 和 res^res1
      
      

4. 位运算符：

   1. 1.&（按位与）参加运算的两个二进制数，同时为1，才为1，否则为0。举例 3&5=1。
      2.|（按位或）参加运算的两个二进制数，一个为1就为1，否则为0。2 | 4=6
      3.^（按位异或）参加运算的两个二进制数，位不同则为1，位相同则为0。6^7=1
      4.~（按位非）需要一个操作数，非运算会将该数的底层二进制码（补码）取反。~ -5 =4
      5.<< （左位移运算符）注：位移补码，而非原码。。。将二进制码整体左移指定位数，左移后空出来的位用“0”填充，例如 -5 << 2 = -20

      6.>>（右位移运算符）与 >>>（无符号右位移运算符）
      >> 把操作数的二进制码右位移指定位数，左边空出来的位以原来的符号位填充。原来是负数就填充1，原来是正数就填充0。符号位不变。

      举例： -5 >> 2 【把 -5 的底层机器数（补码）右移 2位。移动的都是补码，千万别蒙。机器中存储的都是数值的补码形式。】

5. 树：

   1. BST：搜索二叉树
      AVL：平衡搜索二叉树，（子树的高度差不能超过1）