Java--算法--动态规划

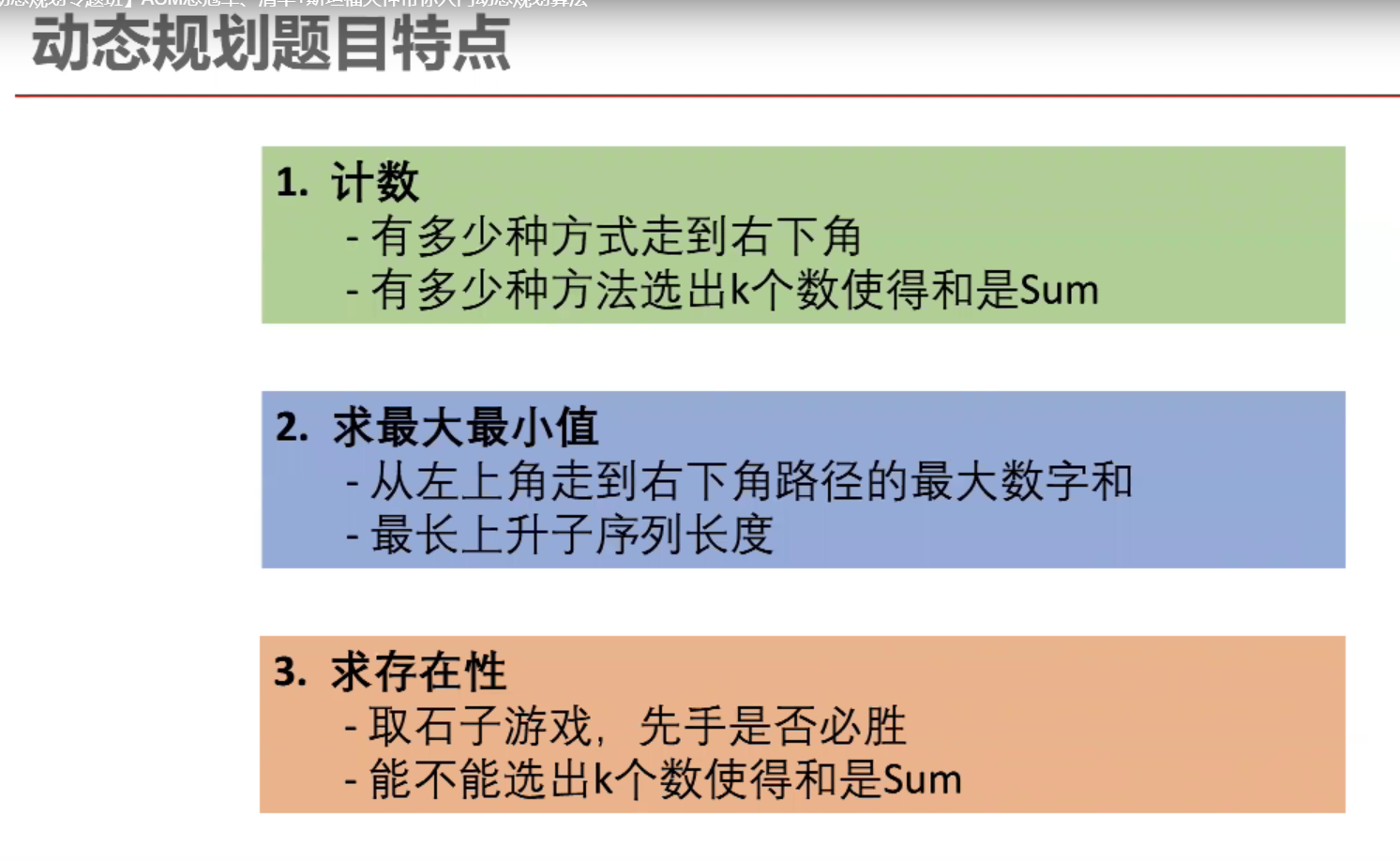
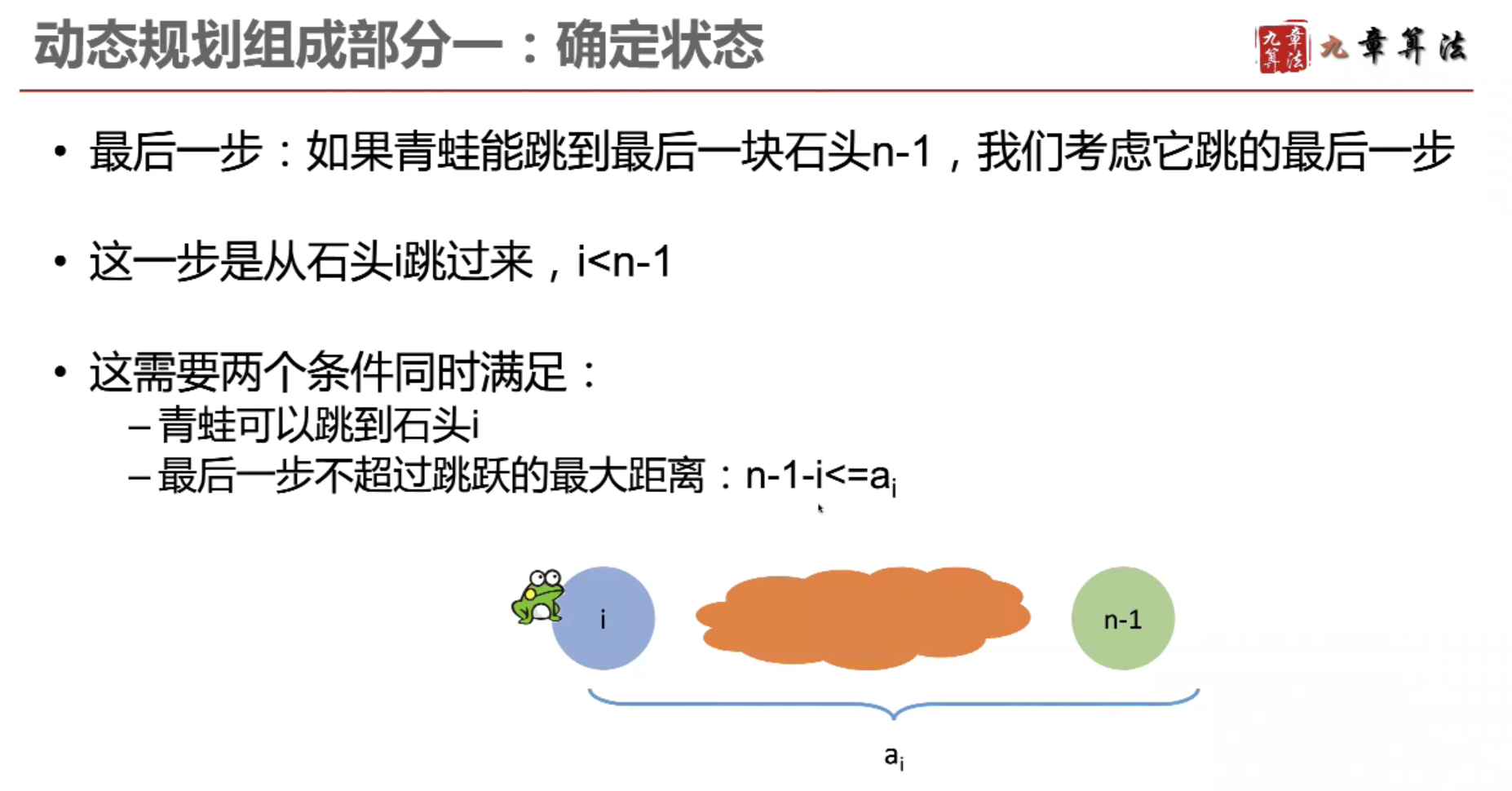
1. 动态规划基本介绍：
   1. 
   2. 
   3. 

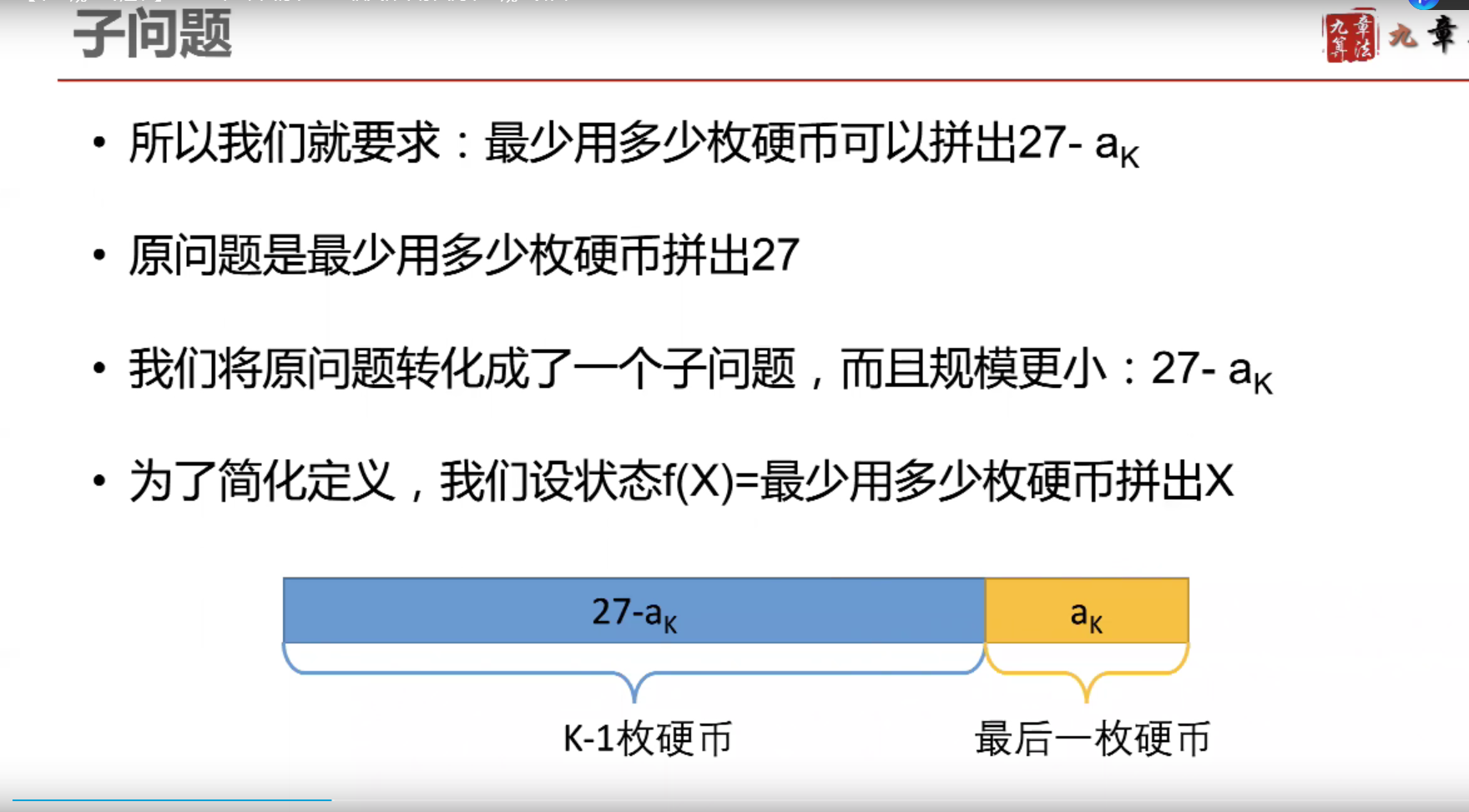
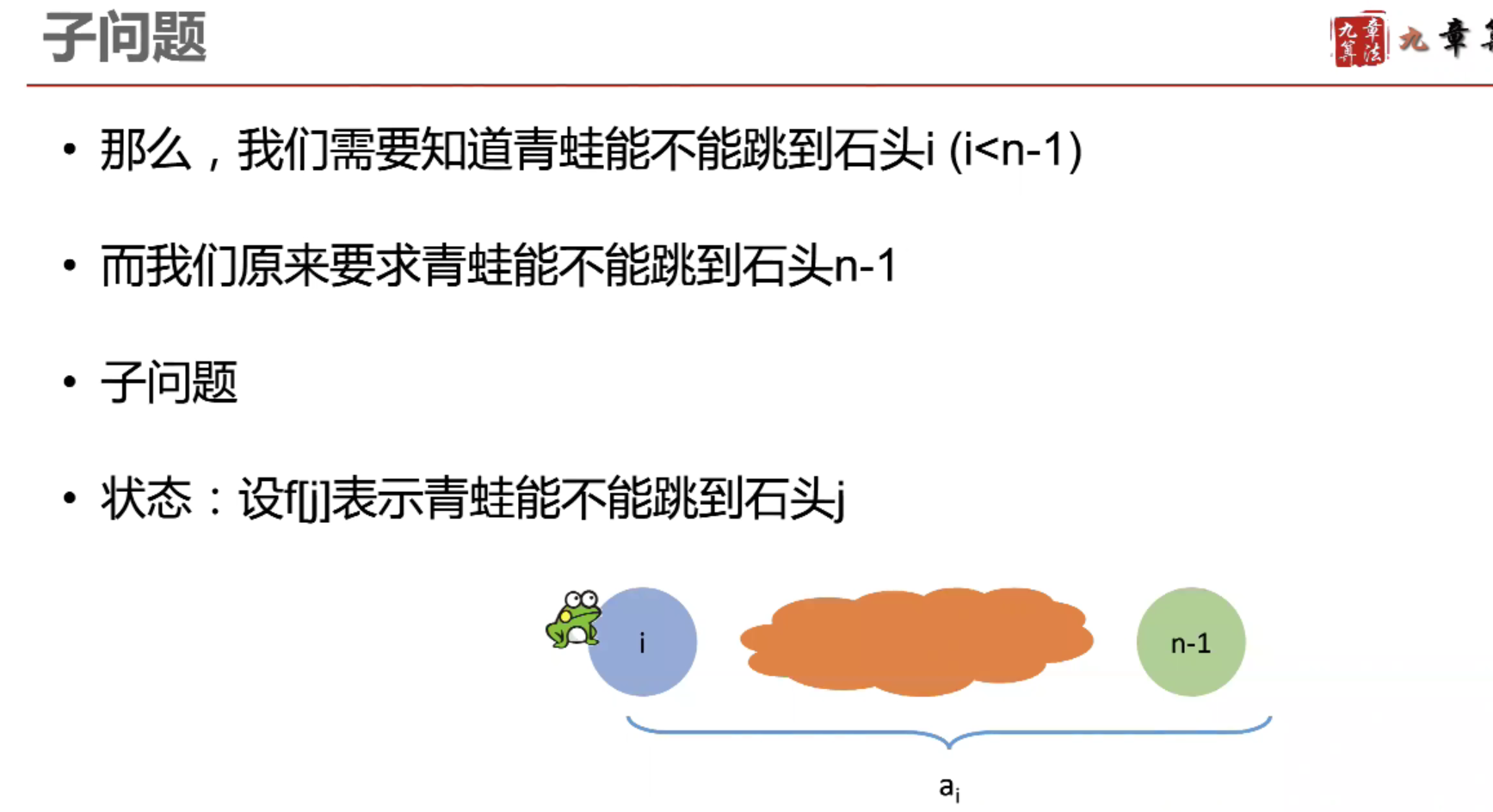
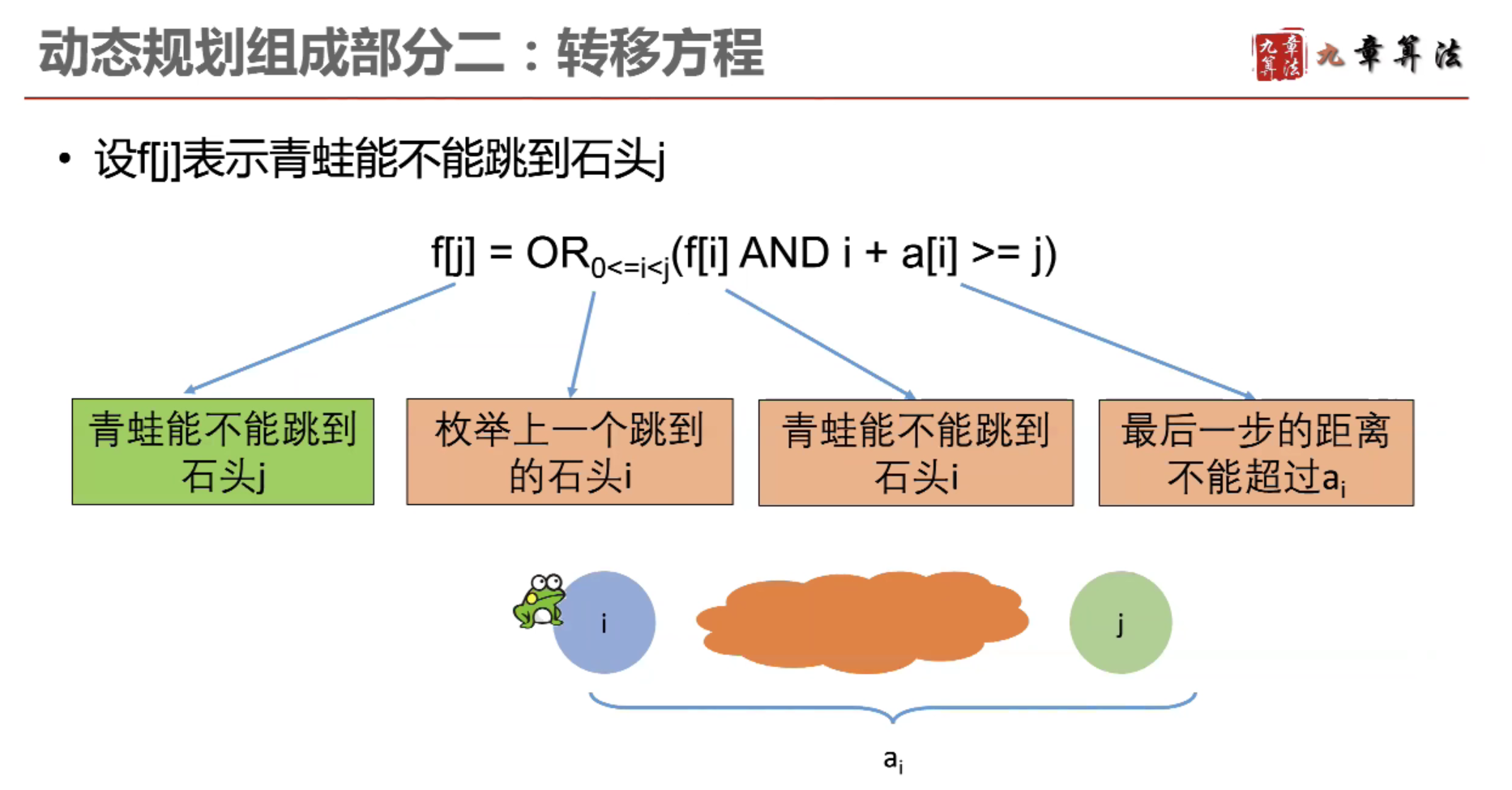
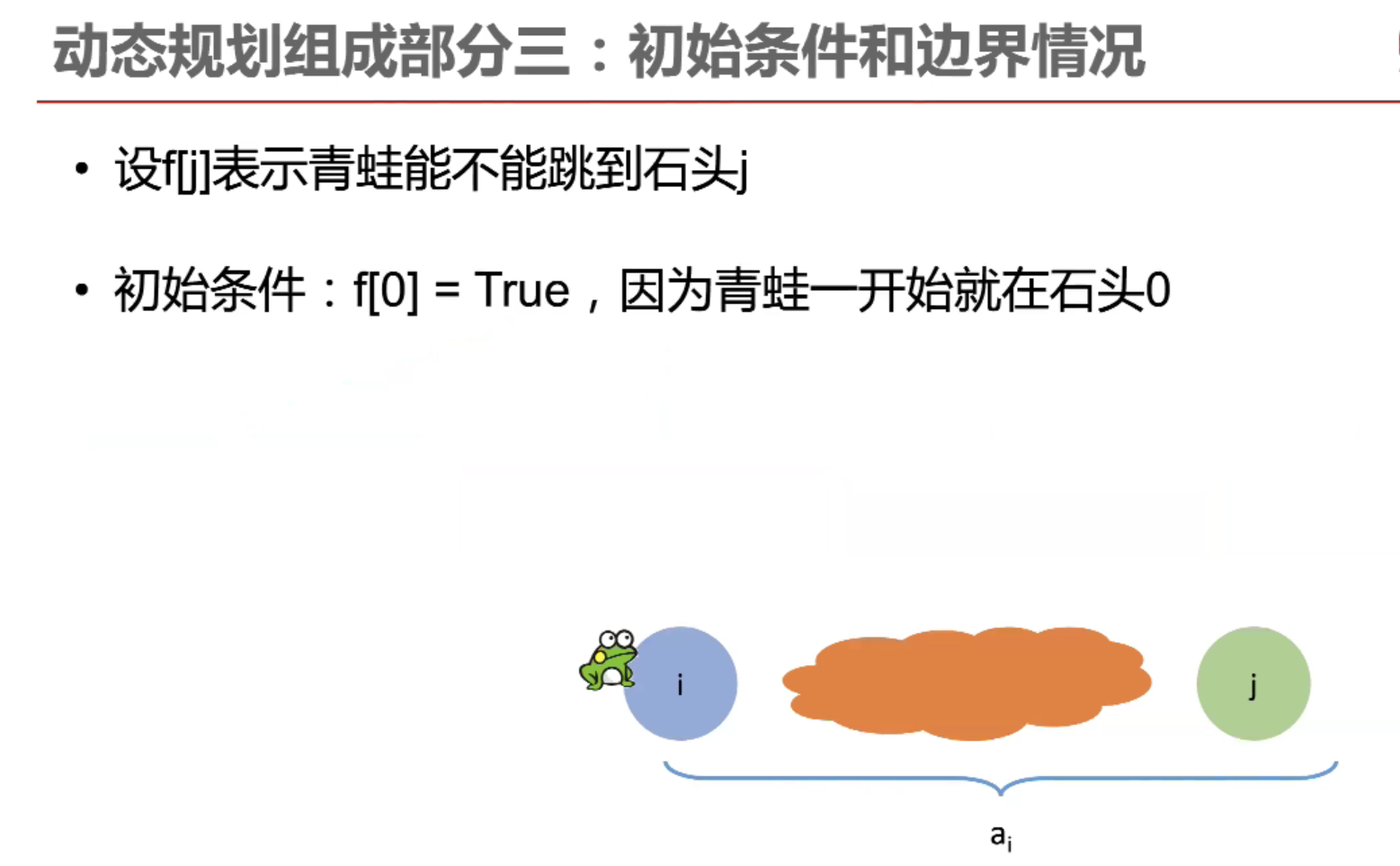
2. 动态规划解题思路：

   1. 

      1. 
      2. 
      3.  

   2. 

       

   3. 

   4. 

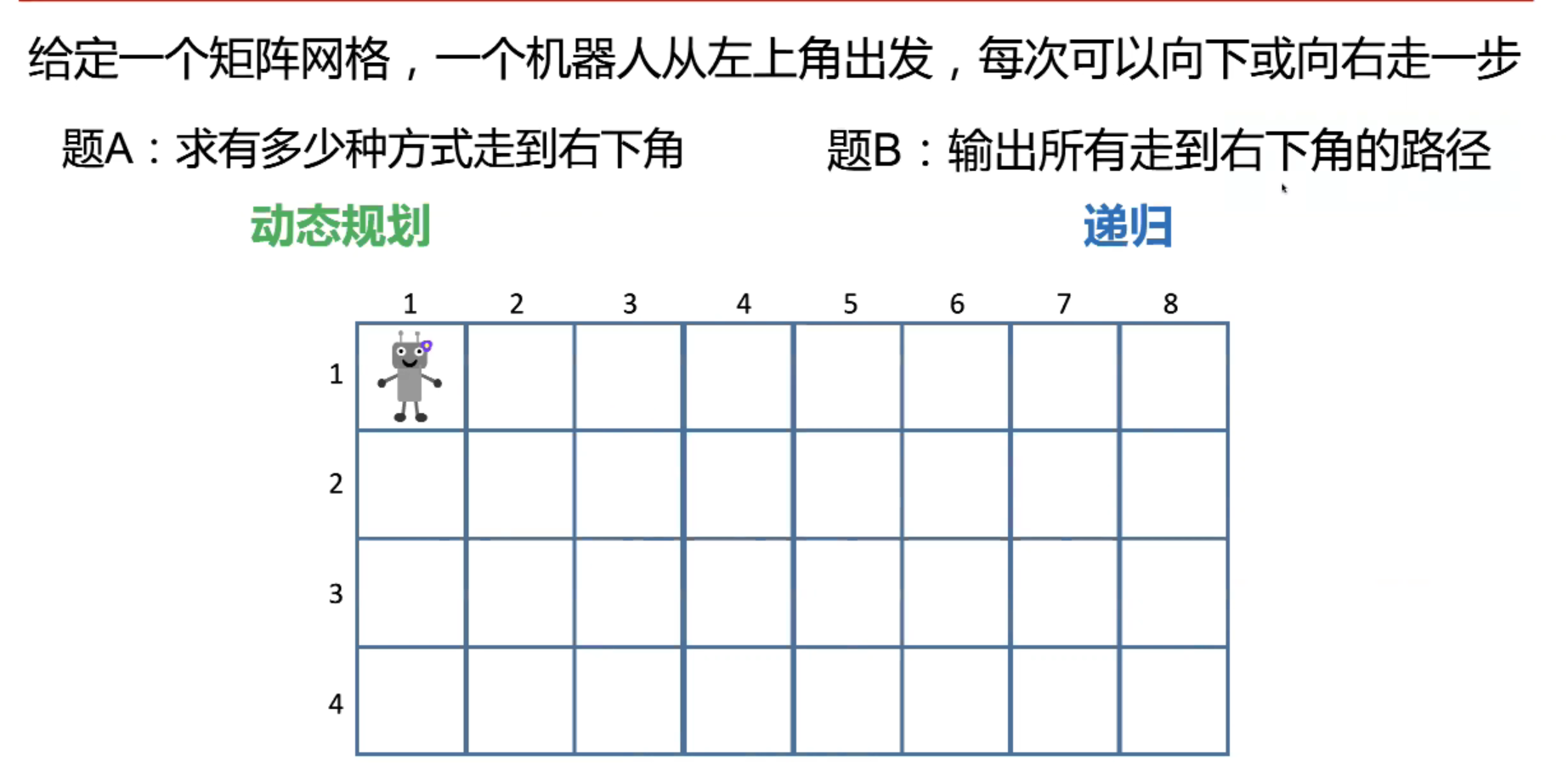
3. 动态规划例题:

   1. 

   2. 
      1. 
   3. 

      1. 

         1. 

      2. 

      3. 

      4. 

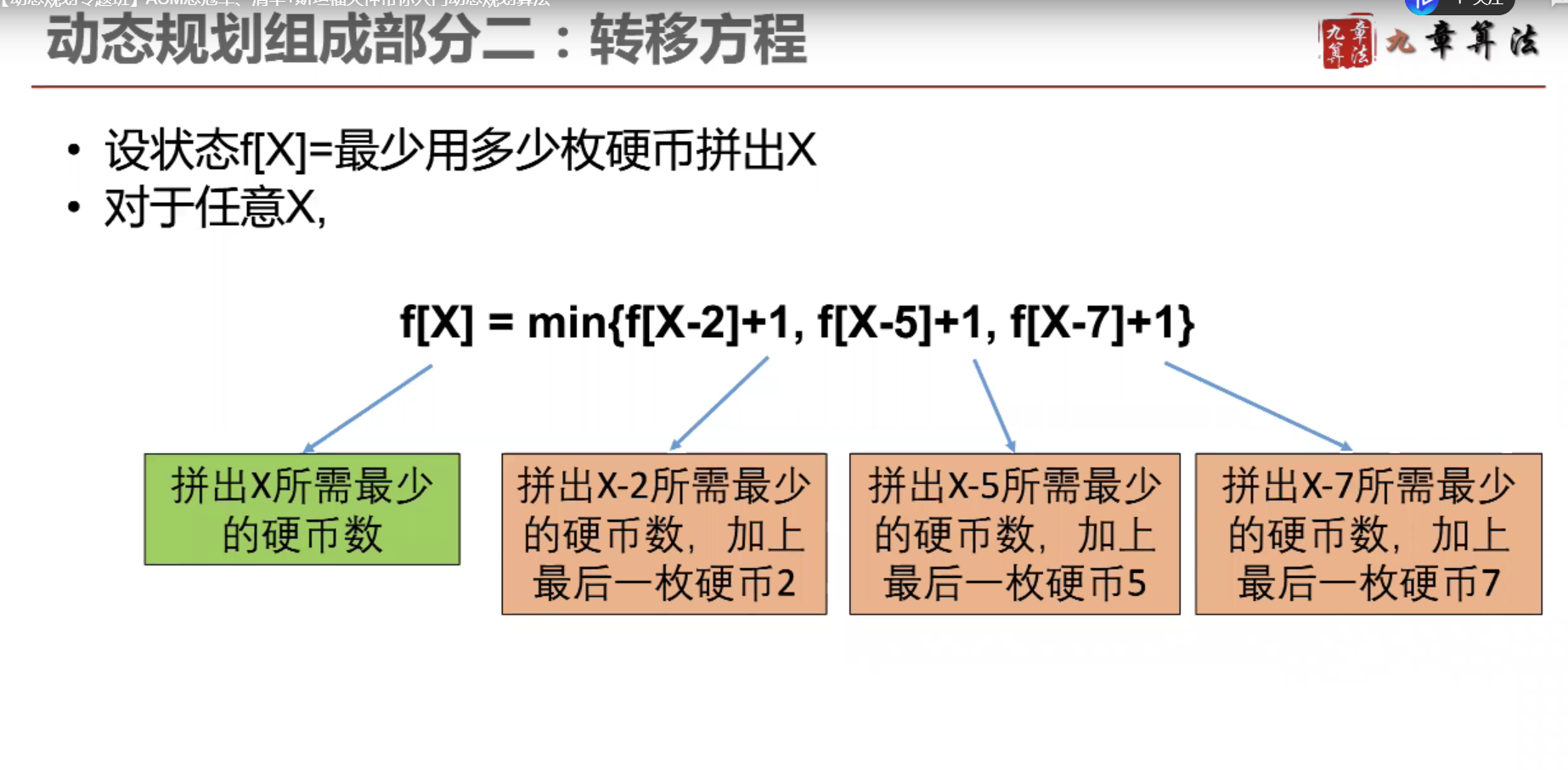
   4. package com.model.dynamic;
      
      import java.util.Arrays;
      
      /**
       * @Description:测试类
       * @Author: 张紫韩
       * @Crete 2021/8/10 11:17
       * 动态规划
       * 怎样组合会是硬币的数量最少,最少的硬币数
       * 1.求最值（给定硬币面值，用最少的硬币数组成 27）
       * 2.计数（从最左上角到右下角有几种走法）
       * 3.是否存在可能性（这一组数之中是否存在几个数之和等于0）
       */
      public class DynamicDemo01 {
          public static void main(String[] args) {
              int[] a = {2, 5, 7};
              System.out.println(count(a, 27));
      
              int[][] f = new int[1][1];
              System.out.println(path(f));
      
              int[] jump={3,2,1,2};
              System.out.println(isJump(jump));
          }
      
          //    f[num]=min{f[num-2]+1,f[num-5]+1,f[num-7]+1}
      //    A：中有所有的硬币面值(2,5,7)
      //    num：我们拼num元
      //    求出用所给的硬币，用最少的数拼出num元
          public static int count(int[] A, int num) {
              int[] f = new int[num + 1];
              Arrays.fill(f, Integer.MAX_VALUE);
              f[0] = 0;
              for (int i = 1; i < f.length; i++) {
                  for (int k : A) {
                      if (i >= k && f[i - k] != Integer.MAX_VALUE) {
                          f[i] = Math.min(f[i - k] + 1, f[i]);
                      }
                  }
              }
              return f[num] == Integer.MAX_VALUE ? -1 : f[num];
          }
      
          //   一个二维数组，从左上角到右下角，只能向右或向下走
      //    求从左上角到右下角有多少种
      //    f[i-1][j-1]=f[i-1][j-2]+f[i-2][j-1]
          public static int path(int[][] f) {
              for (int i = 0; i < f.length; i++) {
                  for (int j = 0; j < f[i].length; j++) {
                      if (i == 0 || j == 0) {
                          f[i][j] = 1;
                      } else {
                          f[i][j] = f[i - 1][j] + f[i][j - 1];
                      }
                  }
      
              }
              return f[f.length - 1][f[0].length - 1];
          }
      
          //跳跃问题，能否跳到n [3,2,1,0,1]
          public static boolean isJump(int[] nums) {
              int n = nums.length;
              boolean[] f = new boolean[n];
              Arrays.fill(f, false);
              f[0] = true;
              for (int i = 1; i < n; i++) {
                  for (int j = 0; j < i; j++) {
                      if (f[j] && i - j <= nums[j]) {
                          f[i] = true;
                          break;
                      }
                  }
              }
              return f[n-1];
          }
      
      }

       

4. 总结

   1.