关于二分与三分(基础)
二分查找:
不再细说,就是在单调的一段区间查找一个数(或比它大(小))的数。
在STL中也有lower_bound,upper_bound两函数可用。
二分查找应用广泛,尤其配合DP中的数据处理上效率极高。
二分答案:
在求解一个形如:最大(小)值最小(大)的问题。显然是从可行解中寻找最优解的过程,那么易知可行解的取值是单调的。
因此我们可以二分范围内的解,若解可行,尝试二分更优解,否则二分较差解。这样以来,当l==r时,我们就找到了最优解。
综上可以看出二分答案的过程实际上就是将求解转化为了解的判定(一般可以O(n)判断),在思维难度和算法复杂度上都有很好的优化。
那么一般来说,二分答案有固定套路,只是在解的判定上有所不同:
while(l<=r) { int mid=(l+r)>>1; if(check(mid))r=mid-1; else l=mid+1; } cout<<l;//最大值最小
while(l<=r) { int mid=(l+r)>>1; if(check(mid))l=mid+1; else r=mid-1; } cout<<r;//最小值最大
当然了,如果不知道输出什么,那就把mid记录下来,最后满足check(mid)==true的mid一定是最优解。
另外的,二分答案可以同DP,贪心等东西联系起来,这里有几道简单的例题:
进击的奶牛
最基础的题,我们只需要二分距离判断如果奶牛间距离最小为mid能否放开全部奶牛就好(当然还需要排序牛棚位置):
bool check(int x) { int before=a[1],total=1; for(int i=2;i<=n;i++) { if(a[i]-before>=x) { before=a[i]; total++; } if(total==c)return 1; } return 0; }
时间管理
我们按照S_i排序,令二分的mid作为初始时间,然后从1开始模拟,如果从某处时间超过了S_i,舍去,反之,可行。
bool check(int x) { int _time=x; for(int i=1;i<=n;i++) { _time+=e[i].t; if(_time>e[i].s)return false; } return true; }
数列分段
我们令二分出的数为x,则需要数列分成m部分且每部分和不大于x。
考虑这样一个贪心:
从头开始累加,直到超过x,则需要多分一部分,当我们考虑过所有数,共分为cnt个部分,那么此解合法当且仅当cnt<=m。正确性显然。
bool check(int x) { int now=0,cnt=1; for(int i=1;i<=n;i++) { if(a[i]>x)return false; if(now+a[i]>x) { cnt++; now=0; } now+=a[i]; } return cnt<=m; }
一元三次方程求解
我们观察一元三次方程的大致图像:

如图便是一个标准情况下的三次函数图像。当a>0时通过观察我们会发现从左到右的趋势是:升——降——升。而当a<0时情况相反。
当然了,输入保证方程有三个解,为了方便观察解的分布,我们绘制样例的图像:
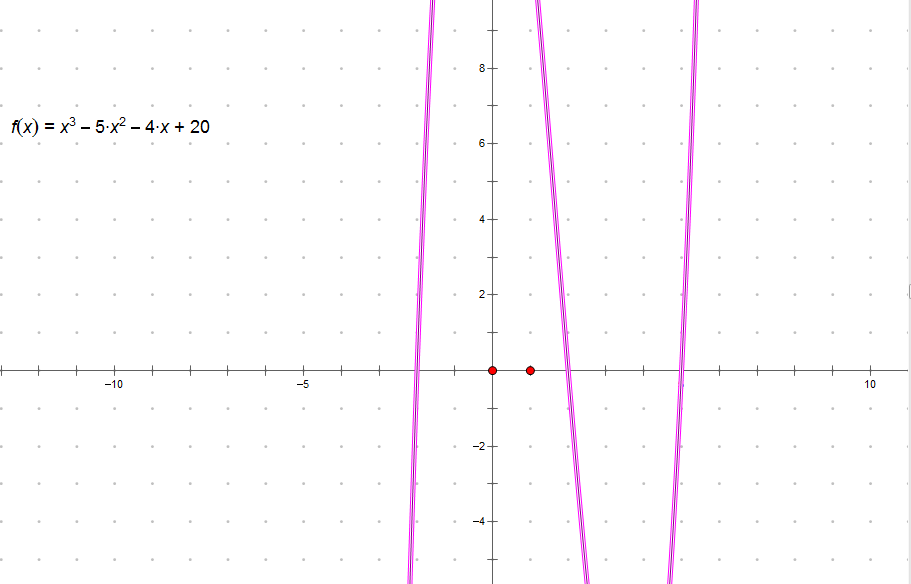
我们发现三个解分别分布在其三个单调区间内,因此我们可以在每个单调区间内二分。
接下来一步是如何求 其单调区间,显然其单调区间为:[-100,x1],[x1,x2],[x2,100];关键就是求函数的两极值点。
考虑求导(逃
导函数f’(x)=3ax^2+2bx+c,求其两零点(题目保证了解的存在性),由公式法知:
x1=(-2*b+sqrt(4*b*b-12*a*c))/(6*a);
x2=(-2*b-sqrt(4*b*b-12*a*c))/(6*a);
对于a<0的情况,为了统一将a变为-a,其余系数也乘-1,方程-ax^3-bx^2-cx-d=0 仍成立,不影响答案。
对于增区间和减区间分别二分求解即可。
这里是之前没有提过的对于实数的二分:
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; double a,b,c,d; const double eps=0.001; double judge(double x) { return a*x*x*x+b*x*x+c*x+d;//带入求值 } double find_up(double l,double r) { while(fabs(r-l)>eps)//控制精度 { double mid=(r+l)/2.0; if(judge(mid)<0)l=mid; else r=mid; } return l; } double find_down(double l,double r) { while(fabs(r-l)>eps) { double mid=(r+l)/2.0; if(judge(mid)<0)r=mid; else l=mid; } return r; } int main() { cin>>a>>b>>c>>d; if(a<0) { a=-a; b=-b; c=-c; d=-d; } double x1=(-2*b+sqrt(4*b*b-12*a*c))/(6*a); double x2=(-2*b-sqrt(4*b*b-12*a*c))/(6*a); printf("%.2f ",find_up(-100.0,x2)); printf("%.2f ",find_down(x2,x1)); printf("%.2f",find_up(x1,100.0)); }
U盘
接口大小直接限制了可选文件的范围,如果接口大小确定,那么可用文件也就确定了。
我们二分接口大小,考虑如何check.
我们对于可用文件跑一个01背包,那么f[s]表示大小为s可获的最大价值。方案可行当且仅当f[s]>=p;
bool check(int x) { memset(f,0,sizeof(f)); for(int i=1;i<=n;i++) if(w[i]<=x) for(int j=s;j>=w[i];j--) f[j]=max(f[j],f[j-w[i]]+v[i]); return f[s]>=p; }
以上是最基础的二分答案例题,想深入理解还要多训练。
三分:
三分法,适用于求解凸性函数的极值问题,
流程:设当前求解区间为[l,r],令m1=l+(r-l)/3,m2=r-(r-l)/3;我们记函数值更优的点为好点,函数值更劣的点为坏点。那么显然最优点和好点会与坏点同侧,我们的求解区间就成了[l,m2],
注:单峰函数必须严格单调,否则f(m1)==f(m2),将无法判定如何缩小左右界
(以上摘自《信息学奥赛一本通·提高篇》 注:良心推荐这本书,你值得拥有!虽然本人在书中找出了几处小错误(手动滑稽),但白璧微瑕,毕竟还是第一版嘛,之后肯定会完善的)
当然了对于二分和三分而言,如果你不想卡精度,那么可以限制二分次数,这里不再赘述。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const double eps=1e-6; double n,l,r; double a[14]; double f(double x) { double ans=0; for(int i=1;i<=n+1;i++) ans+=a[i]*pow(x,n-i+1); return ans; } int main() { cin>>n>>l>>r; for(int i=1;i<=n+1;i++) cin>>a[i]; while(fabs(r-l)>=eps) { double m1=l+(r-l)/3,m2=r-(r-l)/3; if(f(m1)<f(m2))l=m1; else r=m2; } printf("%.5f",r); }

