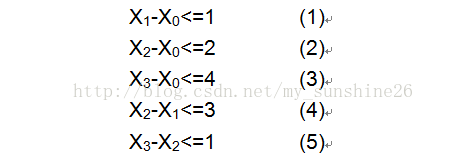差分约束系统

一、概念

差分约束系统（system of difference constraints），是求解关于一组变数的特殊不等式组之方法。如果一个系统由n个变量和m个约束条件组成，其中每个约束条件形如xj-xi<=bk(i,j∈[1,n],k∈[1,m]),则称其为差分约束系统(system of difference constraints)。亦即，差分约束系统是求解关于一组变量的特殊不等式组的方法。

通俗一点地说，差分约束系统就是一些不等式的组，而我们的目标是通过给定的约束不等式组求出最大值或者最小值或者差分约束系统是否有解。(如果一个系统由n个变量和m个约束条件组成，形成m个形如ai-aj≤k的不等式(i,j∈[1,n],k为常数),则称其为差分约束系统。)

二、引例

给定n个变量和m个不等式，每个不等式的形式为 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m， a[k]已知)，求 x[i] - x[j] 的最大值。 例如当n = 4，m = 5，给出如下图所示的不等式组，求x3 - x0的最大值。

一般思路：我们可以尝试把几个不等式组合得到最后我们要求的式子，于是这些式子里最小的那个就是答案。 比如，在这个例子中： （3） --> x3 - x0<=4； （1）（4）（5） --> x3 - x0<=5； （2）（5） --> x3 - x0<=3; 所以最后结果就是3. 在这个过程中，我们是否想到这种方法与我们已经学的一种算法有所联系，是的，就是最短路算法。

三、差分约束与最短路模型

1、与最短路模型的联系

先给出结论：求解差分约束系统，都可以转化成图论的单源最短路径（或最长路径）问题。

我们观察上面例子中的不等式，都是x[i] - x[j] <= a[k]，可以进行移项，成为x[i] <= x[j] + a[k]，我们令a[k] = w(j, i)，dis[i]=x[i],并使i=v,j=u,那么原始就变为：dis[u]+w(u,v)>=dis[v],于是可以联想到最短路模型中的一部分代码

if(dis[u]+w(u,v)<=dis[v])
{
    dis[v]=dis[u]+w(u,v);
}

这不正与松弛操作相似吗？

但是好像不等号方向刚好相反，但其实这并不矛盾

上面的代码要实现的是使dis[u]+w(u,v)>dis[v],而对于不等式，我们进行建边的操作：对于每个不等式 x[i] - x[j] <= a[k]，对结点 j 和 i 建立一条 j -> i的有向边，边权为a[k]，求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路，两者刚好吻合。所以求解差分约束问题就转化为了最短路问题。

2.问题解的存在性

由于在求解最短路时会出现存在负环或者终点根本不可达的情况，在求解差分约束问题时同样存在

（1）、存在负环

如果路径中出现负环，就表示最短路可以无限小，即不存在最短路，那么在不等式上的表现即X[n-1] - X[0] <= T中的T无限小，得出的结论就是 X[n-1] - X[0]的最大值不存在。在SPFA实现过程中体现为某一点的入队次数大于节点数。（貌似可以用sqrt(num_node)来代替减少运行时间）

（2）、终点不可达

这种情况表明X[n-1]和X[0]之间没有约束关系，X[n-1] - X[0]的最大值无限大，即X[n-1]和X[0]的取值有无限多种。在代码实现过程中体现为dis[n-1]=INF。

3、不等式组的转化

做题时可能会遇到不等式中的符号不相同的情况，但我们可以对它们进行适当的转化

（1）方程给出：X[n-1]-X[0]>=T ,可以进行移项转化为： X[0]-X[n-1]<=-T。

（2）方程给出：X[n-1]-X[0]<T, 可以转化为X[n-1]-X[0]<=T-1。

（3）方程给出：X[n-1]-X[0]=T，可以转化为X[n-1]-X[0]<=T&&X[n-1]-X[0]>=T，再利用（1）进行转化即可

4、应用

对于不同的题目，给出的条件都不一样，我们首先需要关注问题是什么，如果需要求的是两个变量差的最大值，那么需要将所有不等式转变成"<="的形式，建图后求最短路；相反，如果需要求的是两个变量差的最小值，那么需要将所有不等式转化成">="，建图后求最长路。 //以上摘自差分约束算法总结