day01-数组理论基础|704.二分查找|27.移除元素
数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合,可以通过下标索引的方式方便的获取到下标对应元素的值。
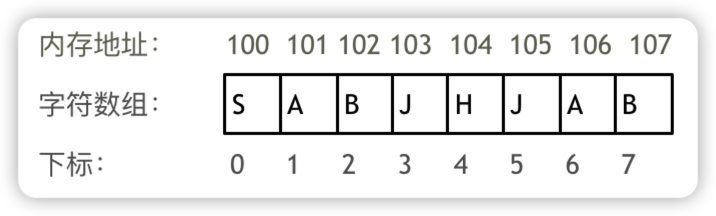
- 数组下标索引是从0开始的
- 数组内存空间地址是连续的,所以在对数组进行增删操作时,只能进行覆盖操作(需要移动后续所有元素)
704.二分查找
leetcode题目链接:https://leetcode.cn/problems/binary-search/
题目描述:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例:
示例一:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4示例二:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
题目解读过程:
该题需要我们从一个有序且无重复的数组中,去搜索对应的值是否存在的问题(返回对应值在数组中的下标);其中的两个特点是满足使用二分法的前提条件:有序 & 无重复元素。
在使用二分法的过程中,涉及到很多区间的判断:
- 循环的结束条件
- 右指针的取值
- 左右指针该如何移动
为了解决区间问题,在解题过程中需要先定义好数组的区间定义(左闭右闭 or 左闭右开),然后在涉及区间判读时通过举例去比对是否满足我们最开始定义的区间。
下面以我个人熟悉的左闭右闭区间为例:
class Solution:
def search(self, nums: List[int], target: int) -> int:
# 定义区间为左闭右闭
left = 0
right = len(nums) - 1 # right需要满足区间定义[ ],所以需要进行-1操作
while(left <= right): # 例如只有一个元素时[1, 1],left=right符合区间定义
middle = left + (right - left) // 2 # 避免left+right的值越界
if(nums[middle] > target): # target在左区间,更新right的值
right = middle - 1 # 因为middle已经比较过了,所以[left, middle-1]
elif(nums[middle] < target): # target在右区间,更新left的值
left = middle + 1 # 因为middle已经比较过了,所以[middle + 1, right]
else:
return middle
return -1
总结:
使用二分法的难点在与边界条件的判断上,所以在一开始做题之前就需要定义好接下来的区间定义,后续在写边界条件时举例去判断是否符合区间的定义。
二分法的时间复杂度为O(logN)。
27.移除元素
leetcode题目链接:https://leetcode.cn/problems/remove-element/
题目描述:给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例:
示例一:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。示例二:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
题目解读过程:
该题需要我们原地的从数组中移除等于val的元素,不能使用额外的数组空间。涉及了两个比较关键的内容:
- 只能在当前数组进行操作
- 需要移除数组中的元素-->数组只能进行覆盖
其本质就是用后面的元素覆盖前面元素的一个操作,解题思路是双指针法:
- 快指针fast用于遍历数组中的元素,并判读是否符合相等的条件
- 慢指针slow用于生成新的数组(本质是一个覆盖的过程)
代码示例:
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
slow = 0 # 定义慢指针的索引下标
for fast in range(len(nums)):
if(nums[fast] != val):
nums[slow] = nums[fast]
slow += 1
return slow



