椭圆光学性质的几何证明
椭圆有个很好的光学性质:从一个焦点发出的光线,都会汇聚到另一个焦点。这种神奇的性质的证明,往往都是通过解析几何来说明。这里介绍一个简单的、只需要几何方法即可说明的证法。
问题描述和证明思路
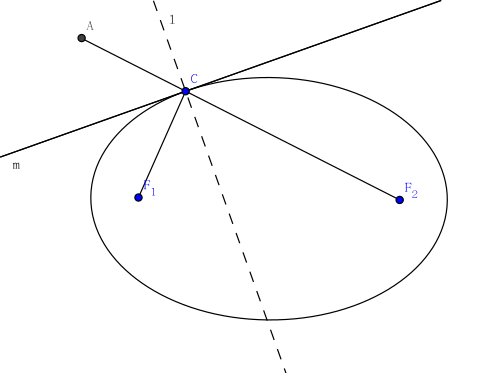
先描述下问题:已知椭圆的半长轴为a,焦点是\(F_1\)和\(F_2\),在椭圆上任选一点C(共线情况好说,这里不妨认为C与\(F_1\)、\(F_2\)不共线),作C的角平分线\(l\),过C点作\(l\)的垂线m,则m是椭圆的切线。
这和高中的一道题有些像:已知有两个村庄F1、F2和河流m,在m上要建一个抽水站P,问P在哪里使得\(PF_1+PF_2\)最小。受到启发,证明如下
证明思路:添加辅助线——作\(CF_1\)关于m的对称线段CA。容易证明A、C、\(F_2\)是共线的。这和抽水站问题很像:如果取m上不是C的点P,则
\[PA+PF_2>CA+CF_2=2a
\]
也就是说,\(PF_1+PF_2\)也要大于2a,即P点要落在椭圆外面。这意味着直线m与椭圆只有一个交点。即m是椭圆的切线。
后记
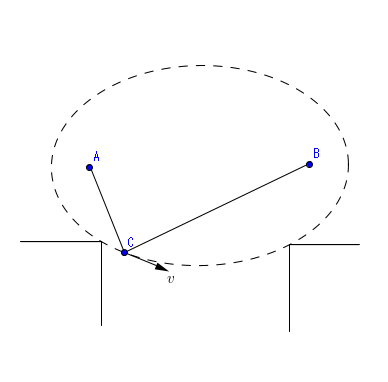
当时遇到了一道物理题,一根2a长的绳子两端固定在两点上,一个人挂在滑轮上从一端滑向另一端。他的轨迹就是椭圆,而速度就是切线。从这个出发突然想到了椭圆的光学性质,可以这样证。
在百度的时候,发现已经有人发表了类似的完整证明,还有其他类型的二次曲线。这里是一些链接:


