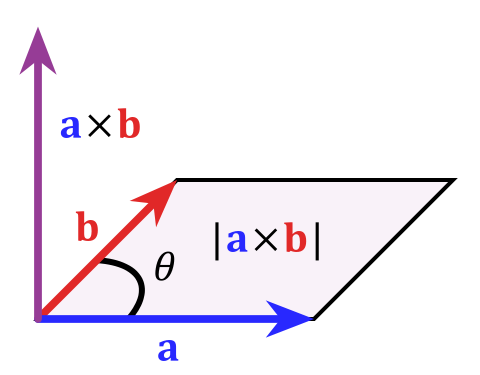
叉乘(向量的外积)是物理里面常常用到的概念, 它是由两个向量得到一个新的向量的运算。一般我们都是从几何意义下手: 向量\(\vec a\)和\(\vec b\)叉乘, 得到一个垂直于\(\vec a\)和\(\vec b\)的向量\(\vec a \times \vec b\), 它的方向由右手螺旋法则确定, 它的长度是\(\vec a\)和\(\vec b\)张开的平行四边形的面积:
\[| \vec a \times \vec b | = |\vec a| \cdot |\vec b| \cdot \sin \theta
\]
其中\(\theta\)是\(\vec a\)和\(\vec b\)的夹角.
![]()
叉乘满足的基本的性质如下:
- \(\vec a \times \vec a = \vec0\), 因为夹角是0, 所以平行四边形面积也是0, 即叉积长度为0
- \(\vec a \times \vec b = - (\vec b \times \vec a)\), 等式两边的叉积等大反向, 模长因为平行四边形不变而相同, 方向因为右手法则旋转方向相反而相反
- \((\lambda \vec a)\times b = \lambda (\vec a \times \vec b)\), 这点比较好想, 因为: ①正数\(\lambda\)数量乘不会影响\(\vec a\)的方向, 所以左右的叉积方向一样; 负数\(\lambda\)使得\(\vec a\)反向了, 但也使得左右叉积方向相反. ②对\(\vec a\)进行缩放, 平行四边形面积也同等缩放.
- \((\vec a+\vec b) \times \vec c = \vec a \times \vec c + \vec b \times \vec c\), 这种分配率是以前最难想象的了.
上述3. 4.两点结合起来, 说明叉乘具有一种线性性质, 再结合2.就是双线性了(同时对左右具有线性性质). 一直以来我都想找到性质4. 的一种几何证明, 可它就像一个过不去的坎, 挡住了我追求完美的心.
每次想到性质4., 都会去想象空间中一点出发的三个随机向量, 然后又叉乘出两个新向量, 一共5个向量, 甚至画图都很难. 这个问题一直持续了很久, 后来某天突然想到, 可以固定一个向量, 剩余的工作在二维投影面完成啊~
结论4的证明
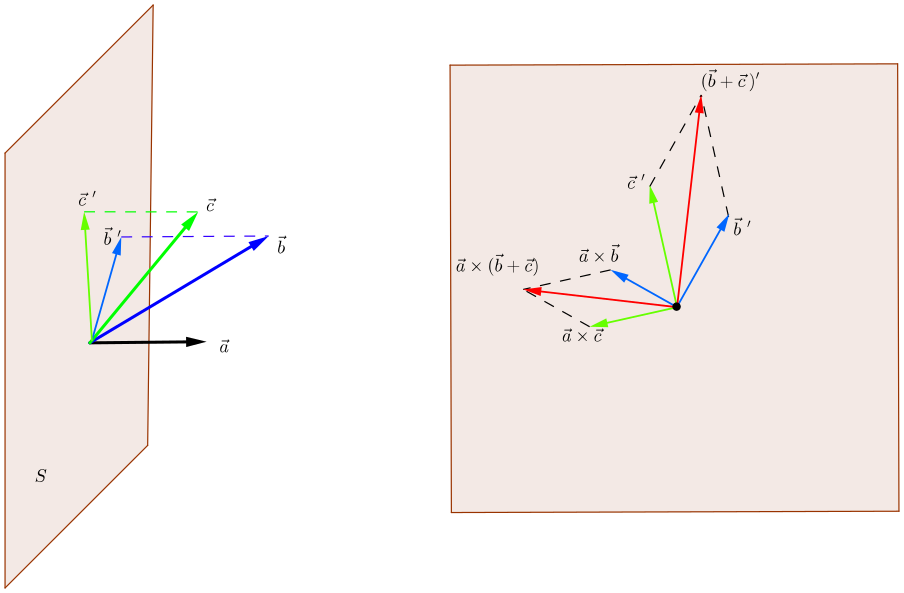
这里证明4.的等价结论: \(\vec a \times (\vec b + \vec c) = \vec a \times \vec b + \vec a \times \vec c\). 如下图所示, 把向量\(\vec b\)和\(\vec c\)按照向量\(\vec a\)的负方向, 投影到与\(\vec a\)垂直的平面S.
![]()
这里先要说明, 向量\(\vec a\)和\(\vec b\)的叉乘, 等于和\(\vec b\)的投影\(\vec b \,'\)的叉乘:
\[\vec a \times \vec b = \vec a \times \vec b \, '
\]
这个结论很好想象, 这种投影其实是把\(\vec b\)掰成与\(\vec a\)垂直的等价部分: 叉乘方向不会变, 并且平行四边形面积不变(底乘高,高没变).
那么这就好说了, 直接在投影面分析:
- \(\vec a \times \vec b\)就是\(\vec b \,'\)逆时针旋转90度, 并且伸缩\(|\vec a|\)(蓝色的向量)
- \(\vec a \times \vec c\)就是\(\vec c\,'\)逆时针旋转90度, 并且伸缩\(|\vec a|\)(绿色的向量)
- \(\vec a \times (\vec b +\vec c)\)就是\(\vec b\,'+\vec c\,'\)逆时针旋转90度, 并且伸缩\(|\vec a|\)(红色的向量)
换句话说, 两个平行四边形是相似的. 在左边那个平行四边形里, 我们得到了结论
\[\vec a \times (\vec b + \vec c) = \vec a \times \vec b + \vec a \times \vec b.
\]
几何证明以后...
所有性质得到几何理解以后, 就感觉整个理论都通畅很多呢...
比如就可以分析, 解析几何下怎么计算叉乘:
\[{\begin{aligned}\mathbf {u} \times \mathbf {v} ={}&(u_{1}\mathbf {i} +u_{2}\mathbf {j} +u_{3}\mathbf {k} )\times (v_{1}\mathbf {i} +v_{2}\mathbf {j} +v_{3}\mathbf {k} )\\={}&u_{1}v_{1}(\mathbf {i} \times \mathbf {i} )+u_{1}v_{2}(\mathbf {i} \times \mathbf {j} )+u_{1}v_{3}(\mathbf {i} \times \mathbf {k} )+{}\\&u_{2}v_{1}(\mathbf {j} \times \mathbf {i} )+u_{2}v_{2}(\mathbf {j} \times \mathbf {j} )+u_{2}v_{3}(\mathbf {j} \times \mathbf {k} )+{}\\&u_{3}v_{1}(\mathbf {k} \times \mathbf {i} )+u_{3}v_{2}(\mathbf {k} \times \mathbf {j} )+u_{3}v_{3}(\mathbf {k} \times \mathbf {k} )\\\end{aligned}}
\]
就是说, 利用前面的分配率, 我们就能够将坐标形式的叉乘归结为基底的叉乘! 对于基底, 我们按照最开始的叉乘定义可以求出他们的值(右手坐标系下):
\[\mathbf {i} \times \mathbf {i} =\mathbf {j} \times \mathbf {j} =\mathbf {k} \times \mathbf {k} =\mathbf {0}
\]
\[\left\{ {\displaystyle {\begin{aligned}\mathbf {i} \times \mathbf {j} &=\mathbf {k} \\\mathbf {j} \times \mathbf {k} &=\mathbf {i} \\\mathbf {k} \times \mathbf {i} &=\mathbf {j} \end{aligned}}} \right.
\quad\quad
\left\{ {\displaystyle {\begin{aligned}\mathbf {j\times i} &=-\mathbf {k} \\\mathbf {k\times j} &=-\mathbf {i} \\\mathbf {i\times k} &=-\mathbf {j} \end{aligned}}} \right.
\]
最后就是熟悉的形式:
\[{\displaystyle {\begin{aligned}
\mathbf {u\times v} &=(u_{2}v_{3}-u_{3}v_{2})\mathbf {i} +(u_{3}v_{1}-u_{1}v_{3})\mathbf {j} +(u_{1}v_{2}-u_{2}v_{1})\mathbf {k} \\
&={\begin{vmatrix}u_{2}&u_{3}\\v_{2}&v_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}u_{1}&u_{3}\\v_{1}&v_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}u_{1}&u_{2}\\v_{1}&v_{2}\end{vmatrix}}\mathbf {k} \\
&={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\\end{vmatrix}}
\end{aligned}}}
\]
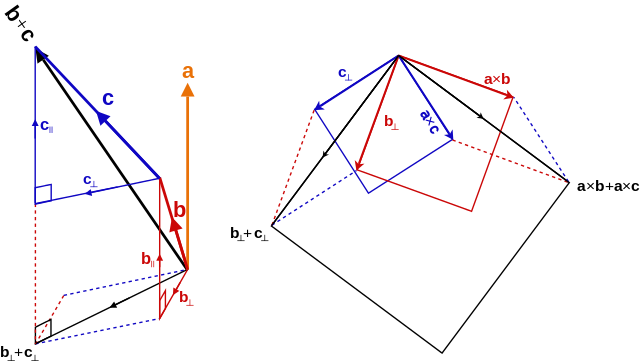
这里再放一张维基百科的图:
![]()
维基百科里还有更多性质的介绍和证明:
https://en.wikipedia.org/wiki/Cross_product


 浙公网安备 33010602011771号
浙公网安备 33010602011771号