LLM学习(3)——搭建知识库

3.1.1 词向量

词向量（Word embedding），又叫Word嵌入式自然语言处理（NLP）中的一组语言建模和特征学习技术的统称，其中来自词汇表的单词或短语被映射到实数的向量。 从概念上讲，它涉及从每个单词一维的空间到具有更低维度的连续向量空间的数学嵌入。

3.1.2 词嵌入

将单词映射到实向量的技术称为词嵌入。

为什么不选择one-hot而要选择更为复杂的word embedding呢：一个主要原因是独热向量不能准确表达不同词之间的相似度，比如我们经常使用的“余弦相似度”。对于向量\(x,y\in R\)，它们的余弦相似度是它们之间角度的余弦：

\[\frac{x^Ty}{|| x |||| y ||}\in \left[ -1,1 \right] \]

由于任意两个不同词的独热向量之间的余弦相似度为0，所以独热向量不能编码词之间的相似性。
word2vec工具是为了解决上述问题而提出的。它将每个词映射到一个固定长度的向量，这些向量能更好地表达不同词之间的相似性和类比关系。word2vec工具包含两个模型，即跳元模型（skip-gram） (Mikolov et al., 2013)和连续词袋（CBOW） (Mikolov et al., 2013)。
任何神经网络或任何监督训练技术的先决条件是具有标记的训练数据。当您没有任何标记数据（即单词及其相应的单词嵌入）时，如何训练神经网络来预测单词嵌入？
我们将通过创建一个“假”任务来训练神经网络来做到这一点。我们不会对这个网络的输入和输出感兴趣，相反，目标实际上只是学习隐藏层的权重，这些权重实际上是我们试图学习的“词向量”。

word2vec

Skip-gram

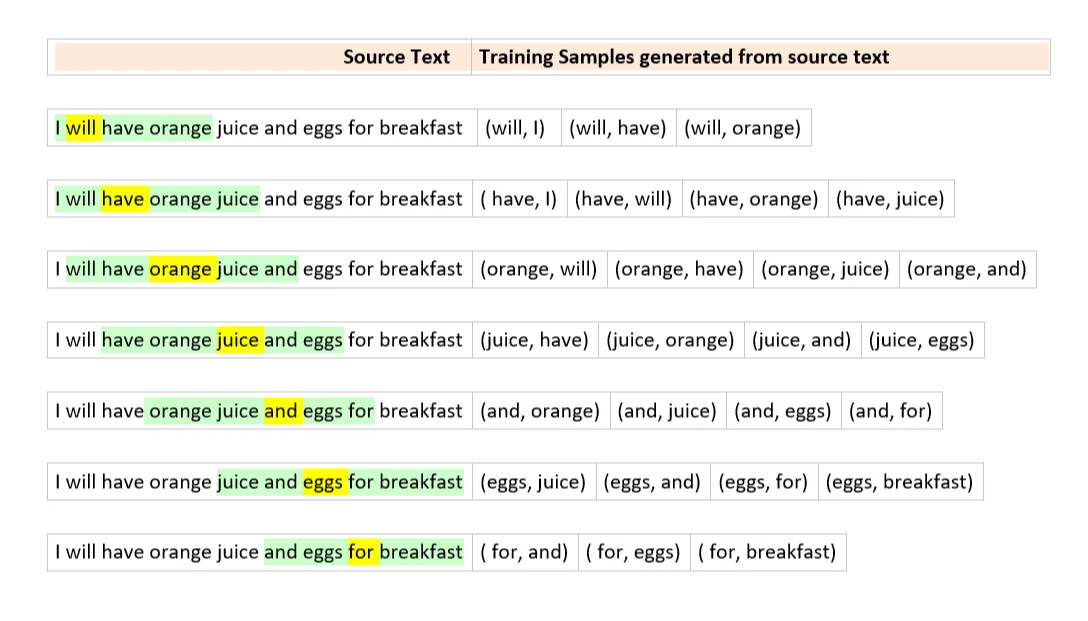
以黄色突出显示的单词是源单词，以绿色突出显示的单词是其相邻单词

Skip-gram 模型的任务是，给定一个单词，我们将尝试预测它的相邻单词，如上图。
如下式，給定中心词 w 和模型参数 θ 要計算上下文 c 出現的几率 p(c|w; θ)，其中 C(w) 表示中心词 w 周围的上下文词的个数。
对于所有的在文本中的中心词 w 我们希望可以通过更新模型参数 θ ，最大化上下文词语的出现的概率的乘积，此时的 θ 就是我们需要的词向量，词向量并不是某个NN的结果而是中间层，且一般为一个浅层的NN。

\[arg\max_{\theta} \prod_{\omega \in Text}{\left[ \prod_{c\in C\left( \omega \right)}{p\left( c|\omega ;\theta \right)} \right]} \]

其条件概率可以通过点积然后softmax进行建模，其中\(\omega\)是中心词，c为上下文词，

\[p\left( c|\omega ;\theta \right) =\frac{e^{v_c\cdot v_{\omega}}}{\sum_{c^{'}\in V}{e^{v_{c^{'}}\cdot v_{\omega}}}} \]

为了得到需要的\(\theta^*\)我们需要使用maximum log likelihood:

\[\arg\max_{\theta}\sum_{(w,c)\in D}\log p(c|w)=\sum_{(w,c)\in D}(\log e^{v_c\cdot v_w}-\log\sum_{c'}e^{v_{c'}\cdot v_w}) \]

另外还需要注意的一点是Text中的每一个词语都可以有两个身份分别是作为中心词和作为上下文词出现所有在实际的操作中，
word2vec将为每个词都预设两个向量(中心词向量矩阵 W & 上下文向量矩阵 W')下面是实际的流程：

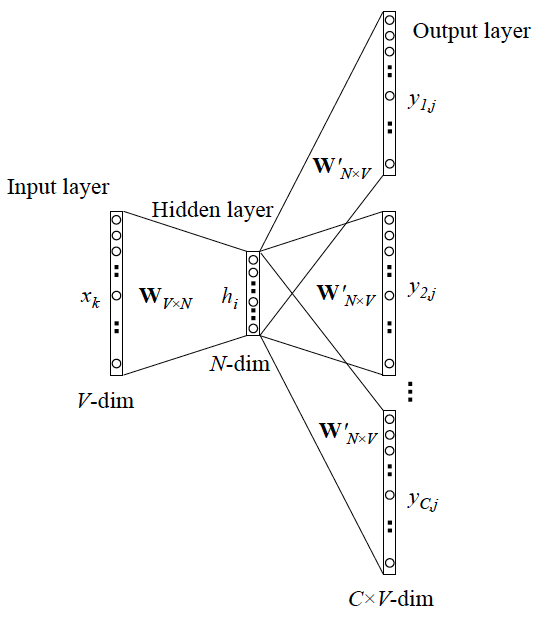
  1. input layer 为中心词 \(x_k\) 的 1-hot vector，维度 1 x V。
  2. 通过预先初始化好的权重 W，W 的大小为上下文窗口 V 与词向量维度 N ，V x N 的矩阵，此 W 训练完成后，就是我们需要的词向量矩阵
  3. 完成第二步后， hidden layer 获得中心词维度 N 的词向量。
  4. 从 hidden layer 到 output layer 做了 C 次的前向传播，每次的传播都与 W’产生 V 維的向量 y，这里的 W' 表示上下文的词向量矩阵，这样的话通过进行C次传播，可以使得在一定窗口大小内的词向量的位置具有一定的影响，再通过更改窗口的尺寸去更新这种影响(个人见解不敢保证准确)，W'不同于 W 的是当词语的身份是是上下文时，才会对应到到此向量,而且W'中包含的不仅仅是上下文词出现的信息还有出现的位置c的信心(但是我不确定的是这种位置信息怎么读取或者说他在这里是可以读取的吗)；而 C 表示该中心词语的上下文数量，通过 window size 決定(2*window size)。
  5. 将这 C 次所产生的值 Softmax function 转换，这里要注意的是，Softmax 分母的计算是由结果的每一个维度而來，而非只通过对应維度，因此我们可以將结果的每一个维度值视为所有上下文词语与中心词的点积，点积越大，概率值就越大。
  6. 由于 \(y_1\) 到 \(y_C\) 都是 \(x_k\) 的上下文词，因此给定中心词 \(x_k\) 我们要最大化 \(y_1\) 到 \(y_C\) 的条件概率值，而每一个条件概率值就以 Softmax 來模拟。
    [注意:实际上这不是一个网络而应该是C个网络不过他们的W权重是相同的，但是 \(W^{'}\)应该分为\(W^{'}_c\)去确定位置，y_{kj}其实指的是k位置j词作为上下文的概率]

CBOW

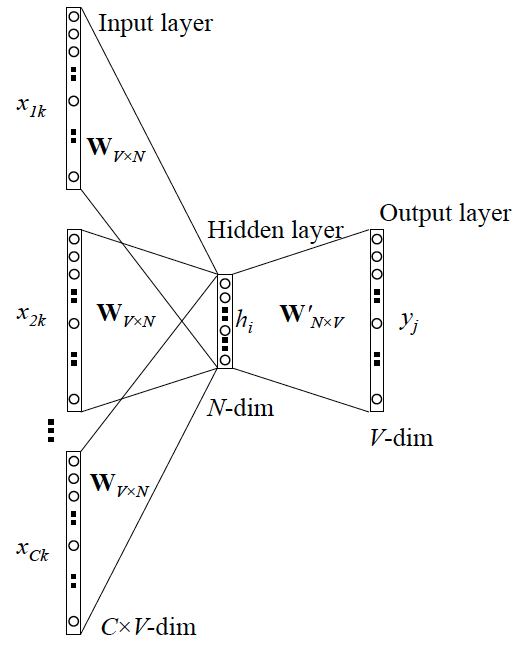
连续词袋（CBOW）模型类似于跳元模型。与跳元模型的主要区别在于，连续词袋模型假设中心词是基于其在文本序列中的周围上下文词生成的。由于连续词袋模型的输入存在多个上下文词，所以我们在计算条件概率时对这些上下文词向量进行平均如式

\[P(w|c^{(1)},c^{(2)},c^{(3)},\ldots,c^{(C)})=\frac{\exp\left(v_{\omega}^\top\bar{v}_c\right)}{\sum_{i\in V}\exp\left(v_{\omega_i}^\top\bar{v}_c\right)} \]

相当于我们需要

\[arg\max_{\theta}\sum_{v=1}^V\log P(w^{(v)}\mid c^{(v-\frac{C}{2})},\ldots,c^{(v-1)},c^{(v+1)},\ldots,c^{(v+\frac{C}{2})}) \]

这里的意思是我们要最大化给定上下文词，所有中心词出现的概率

加速计算

负采样

负采样修改了目标函数。给定中心词\(\omega\)的上下文窗口,任意上下文词\(c\in C\)是由以下建模概率的事件

\[P(D=1|c,w)=\sigma(v_c^Tv_\omega) \]

考虑最大文本化序列中所有这些事件的联合概率\(V\)是文本总词数,C为上下文词数(C=2*window_size):

\[\prod_{v=1}^V\prod_{-\frac{C}{2}\leq i\leq\frac{C}{2},c\neq0}P(D=1\mid w^{(v)},c^{(v+i)}) \]

对一个正样本，考虑一个小的负样本集合，也就是随机选择一个负单词集合（也就是若干非上下文的单词组成的一个子集）

\[P(c^{(v+i)}\mid w^{(v)})=P(D=1\mid w^{(v)},c^{(v+i)})\prod_{k=1,c^k\sim P(\omega) }P(D=0\mid w^{(v)},c^k) \]

然后取对数，计算似然函数损失

\[-\log P\left( c^{v+i}\mid \omega ^v \right) =-\log \sigma \left( {v^T}_{c^{v+i}}v_{\omega ^v} \right) -\sum_{\omega ^k\sim P\left( \omega \right)}{\log \sigma}\left( -v_{c^k}v_{\omega ^v} \right) \]

层序Softmax

Huffman Tree (哈夫曼树)
哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树

作者利用霍夫曼编码 (huffman coding) 來建立二元树，通过统计每个词的出现频率，来决定词的编码，词频越高，编码越短，从而实现对数据的高效压缩。

每个节点都有一个可训练的参数 θ，分别与输入 X_w 点积后作为 sigmoid 函数的输入，根据 sigmoid 的特性其输出介于0-1之间，所以，可依据 sigmoid 的输出值靠近 1 或靠近 0，来决定要往右或往左走

\[\sigma(X_\omega^T\theta)=\frac{1}{1+e^{-X_\omega^T\theta}} \]

可以把条件概率写为
这里的\(d_j^\omega\)是预先对词进行的Huffman编码用于确定我们需要最大化向左还是向右的概率

\[p(d_j^\omega|X_\omega,\theta_{j-1}^\omega)=\begin{cases}\sigma(X_\omega^T\theta_{j-1}^\omega),d_j^\omega=0;\\1-\sigma(X_\omega^T\theta_{j-1}^\omega),d_j^\omega=1;\end{cases} \]

可以等价为

\[p(d_j^\omega|X_\omega,\theta_{j-1}^\omega)=\begin{bmatrix}\sigma(X_\omega^T\theta_{j-1}^\omega)\end{bmatrix}^{1-d_j^\omega}\cdot\begin{bmatrix}1-\sigma(X_\omega^T\theta_{j-1}^\omega)\end{bmatrix}^{d_j^\omega} \]

计算似然函数

\[\begin{gathered} L=\sum_{\omega\in C}log\prod_{j=2}^{l^\omega}\{\left[\sigma(X_\omega^T\theta_{j-1}^\omega)\right]^{1-d_j^\omega}\cdot\left[1-\sigma(X_\omega^T\theta_{j-1}^\omega)\right]^{d_j^\omega}\} \\ =\sum_{\omega\in C}\sum_{j=2}^{l^{\omega}}\{(1-d_{j}^{\omega})\cdot log[\sigma(X_{\omega}^{T}\theta_{j-1}^{\omega})]+d_{j}^{\omega}\cdot log[1-\sigma(X_{\omega}^{T}\theta_{j-1}^{\omega})]\} \end{gathered}\]

Glove

GloVe 本质上是一个具有加权最小二乘目标的对数双线性模型。该模型的主要直觉是一个简单的观察，即词与词共现概率的比率有可能编码某种形式的含义。例如，考虑目标词 ice 和 steam 与词汇表中各种探测词的共现概率。以下是来自 60 亿个单词语料库的一些实际概率：

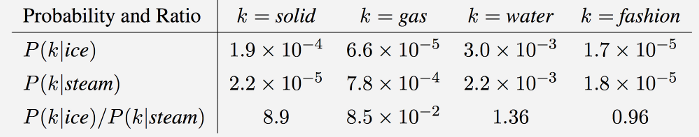
正如所预料的那样，冰与固体的共生频率高于与气体的共生频率，而蒸汽与气体的共存频率高于固体的共存频率。这两个词经常与它们的共同属性水同时出现，并且都很少与不相关的词时尚同时出现。只有在概率比率中，来自水和时尚等非歧视性词语的噪音才会被抵消，因此大值（远大于 1）与冰的特定属性密切相关，而小值（远小于 1）与蒸汽的特定属性密切相关。这样，概率比编码了与热力学相的抽象概念相关的某种粗略的意义形式。

于是基于上面的发现我们可以假设存在于一个未知的函数\(F\)

\[F(\omega_i,\omega_j,\omega_k)=\frac{P_{ik}}{P_{jk}} \]

经过推导可得到\(F\)的形式和\(J\)
推导过程见:通俗易懂理解——Glove算法原理
因为共现概率的比值是标量，所以我们要求是标量函数，因此我们改进为：

\[F((\omega_i-\omega_j)^T\cdot\omega_k)=\frac{P_{ik}}{P_{jk}} \]

公式左边是差右边为商
我们自然而然的可以得到\(F\)的一个选择为exp,那么公式可转换为

\[exp(w_i^Tw_k-w_j^Tw_k)=\frac{exp(w_i^Tw_k)}{exp(w_j^Tw_k)}=\frac{P_{ik}}{P_{jk}} \]

现在我们选择\(exp(w_i^Tw_k)=\alpha P_{ik}=\alpha \frac{X_{ik}}{X_i}\)
两边取对数可得到:

\[w_i^Tw_k=log\alpha +logX_{ik} -logX_i \]

这样模型就引入了两个偏置项(bias)
再计算加权平方误差就可以得到如下公式

\[J=\sum_{ik}f(X_{ik})(w_i^Tw_k+b_i+b_k-logX_{ik})^2 \]

加权函数为

\[\left.f(x)=\left\{\begin{array}{c}(\frac{x}{x_{max}})^\alpha,ifx<x_{max}\\\\1,otherwise\end{array}\right.\right. \]

加权函数的选择Glove的作者给出了一种比较好的选择为:\(x_{max}=100,\beta=\frac{3}{4}\)

下图为原论文中glove对比CBOW和SG的结果，可以看出存在明显的优势。

SVD(矩阵分解)+共现矩阵

首先我们先了解SVD的概念:
SVD分解将任意矩阵分解成一个正交矩阵和一个对角矩阵以及另一个正交矩阵的乘积。对角矩阵的对角元称为矩阵的奇异值，可以证明，奇异值总是大于等于0的。当对角矩阵的奇异值按从大到小排列时，SVD分解是唯一的。

\[A=U\Sigma V^T \]

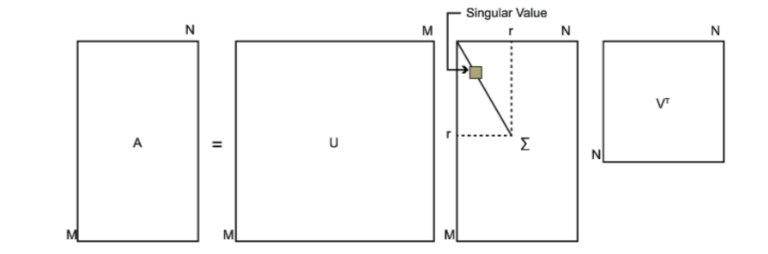
可以推出:

\[AA^T=(U\Sigma V^T)(V\Sigma^TU^T)=U(\Sigma\Sigma^T)U^T \]

\[U^TAA^TU=\Sigma\Sigma^T \]

\((\Sigma\Sigma^T){\text{依然是对角矩阵，又U为正交矩阵。}}\)
所以\((\Sigma\Sigma^T)\)为\(AA^T\)的相似对角矩阵，其对角元为\(AA^T\)的特征值，\(U\)由其对应特征向量构成，这些向量称为A的左奇异向量。
因此\(\Sigma\)的对角元为\(AA^T\)特征值的平方根，称之为矩阵A的奇异值。
类似地\(V\)由\(A^TA\)的特征向量构成，这些向量称为A的右奇异向量。
简单来说我们对\(AA^T\)和\(A^TA\)进行特征值分解，得到的特征矩阵分别就是\(U\)和\(V\),然后对\((\Sigma\Sigma^T)\)的对角线取平方根就可以了
另外\((\Sigma\Sigma^T)\)和\((\Sigma^T\Sigma)\)在是不相等的，两者的维度不相同，但是两者对角线的值是一样的。
\(\Sigma \Sigma^T\)和\(\Sigma^T \Sigma\)在矩阵的角度上是不相等的，因为它们的维度不同。\(\Sigma \Sigma^T\)是一个\(m \times m\)的矩阵，而\(\Sigma^T \Sigma\)是一个\(n \times n\)的矩阵，其中\(m\)是\(A\)的行数，\(n\)是\(A\)的列数。
设

\[\Sigma = \begin{bmatrix} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_r \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{bmatrix} \]

其中\(r\)是\(A\)的奇异值个数。
则

\[\Sigma \Sigma^T = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_r^2 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \end{bmatrix} \]

\[\Sigma^T \Sigma = \begin{bmatrix} \sigma_1^2 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & \sigma_2^2 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_r^2 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \end{bmatrix} \]

这样我们就可以使用三个矩阵去代表一个矩阵(听起来工作还增加了 ？）但是对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

\[A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^{T}\approx U_{m\times k}\Sigma_{k\times k}V_{k\times n}^{T} \]

其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵,实现了降维操作(感觉和PCA有异曲同工之妙)
下面介绍共现矩阵
我们定义一个window_size，来对称的寻找出现在某个单词周围单词的频数，最后把他们汇总为一个矩阵。
例如我们有下列语料库设置window_size=1:

  • I love you
  • I like deep learning
  • I like cats
    那么我们就可以得到
I love you like deep learning cats
I 0 1 0 2 0 0 0
love 1 0 1 0 0 0 0
you 0 1 0 0 0 0 0
like 2 0 0 0 1 0 1
deep 0 0 0 1 0 1 0
learning 0 0 0 0 1 0 0
cats 0 0 0 1 0 0 0
接着我们对共现矩阵进行SVD降维、可视化，依然呈现出了类似Word2Vec的效果。结果如下: 
import numpy as np
import matplotlib.pyplot as plt
la=np.linalg
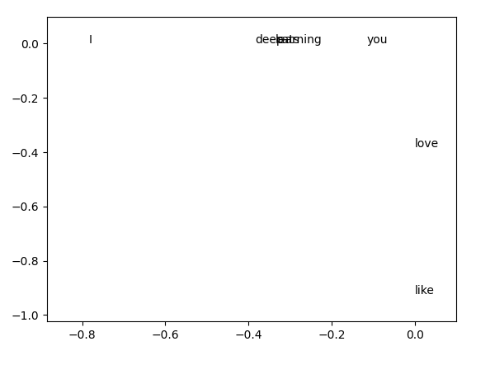
words=["I","love","you","like","deep","learning","cats"]
x=np.array([[0,1,0,2,0,0,0],[1,0,1,0,0,0,0],[0,1,0,0,0,0,0],[2,0,0,0,1,0,1],[0,0,0,1,0,1,0],[0,0,0,1,0,0,0],[0,0,0,1,0,0,0]])

U,s,Vh=la.svd(x,full_matrices=False)
scale_factor = 10
plt.xlim(np.min(U[:, 0])-0.1, np.max(U[:, 0])+0.1)
plt.ylim(np.min(U[:, 1])-0.1, np.max(U[:, 1])+0.1)
for i in range(len(words)):
    plt.text(U[i,0],U[i,1],words[i])
plt.show()

3.2.1 Embedding API 使用

如何使用API见LLM学习(2)——使用 LLM API 开发应用(传送门)

result = genai.embed_content(
    model="models/text-embedding-004",
    content="What is the meaning of life?",
    task_type="retrieval_document",
    title="Embedding of single string")

# 1 input > 1 vector output
print(str(result['embedding'])[:50], '... TRIMMED]')
print(result)
print(type(result))
print(type(result['embedding']))
#结果如下

3.2.2 检索

#导入数据，并且切割，这里并没有对数据进行清洗只是简单的进行了文档的分割
file_paths = []
folder_path = '.\\data'
for root, dirs, files in os.walk(folder_path):
    for file in files:
        file_path = os.path.join(root, file)
        file_paths.append(file_path)
print(file_paths)

from langchain_community.document_loaders import PyPDFLoader
from langchain_community.document_loaders import UnstructuredMarkdownLoader

# # 遍历文件路径并把实例化的loader存放在loaders里
loaders = []

for file_path in file_paths:

    file_type = file_path.split('.')[-1]
    if file_type == 'pdf':
        loaders.append(PyPDFLoader(file_path))
    elif file_type == 'md':
        loaders.append(UnstructuredMarkdownLoader(file_path))

# 下载文件并存储到text
texts = []

for loader in loaders: texts.extend(loader.load())

text = texts[1]
print(f"每一个元素的类型：{type(text)}.", 
    f"该文档的描述性数据：{text.metadata}", 
    f"查看该文档的内容:\n{text.page_content[0:]}", 
    sep="\n------\n")


from langchain.text_splitter import RecursiveCharacterTextSplitter

# 切分文档
text_splitter = RecursiveCharacterTextSplitter(
    chunk_size=500, chunk_overlap=50)

split_docs = text_splitter.split_documents(texts)

结果:

#向量库构建
from langchain_google_genai import GoogleGenerativeAIEmbeddings

os.environ["GOOGLE_API_KEY"] = "AIzaSyBZFSrCWg7Ow2D3I2rMbf37qXp1SlF9T5k"

# 这里无法使用004可能是因为还没有适配？？？
embeddings = GoogleGenerativeAIEmbeddings(model="models/embedding-001",task_type="retrieval_document")
下
## 建立一个用来存放chroma数据库的文件夹
# if not os.path.isdir(".\data\vector_db\\chroma"):                   
#     os.makedirs(".\\data\\vector_db\\chroma")  

## 下面是查看API可以调用的model但是好像不能查看embedding的model
# for m in genai.list_models():
#   if 'generateContent' in m.supported_generation_methods:
#     print(m.name)

from langchain_community.vectorstores import Chroma

vectordb = Chroma.from_documents(
    documents=split_docs[:20], 
    embedding=embeddings,
    persist_directory=".\\data\\vector_db\\chroma"
)

vectordb.persist()

print(f"向量库中存储的数量：{vectordb._collection.count()}")

#相似检索
question="什么是大语言模型"
sim_docs = vectordb.similarity_search(question,k=3)
print(f"检索到的内容数：{len(sim_docs)}")
for i, sim_doc in enumerate(sim_docs):
    print(f"检索到的第{i}个内容: \n{sim_doc.page_content[:200]}", end="\n--------------\n")
# MMR检索
mmr_docs = vectordb.max_marginal_relevance_search(question,k=3)
for i, sim_doc in enumerate(mmr_docs):
    print(f"MMR 检索到的第{i}个内容: \n{sim_doc.page_content[:200]}", end="\n--------------\n")

下面是两种检索的结果:(都蛮古怪的)

补充

PCA和SVD之间有着密切的联系。实际上，PCA可以被视为对数据矩阵进行SVD分解后的特例。具体来说假设我们的样本是m * n的矩阵X，如果我们通过SVD找到了矩阵 \(X^TX\) 的最大的k个特征向量组成的m * d维矩阵U，则我们进行如下处理：

\[X_{d\times n}^{\prime}=U_{d\times m}^TX_{m\times n} \]

可以得到一个d * n的矩阵X，且这个矩阵和我们原来的m * n维的样本矩阵X相比，行数从m剪到了K，可见对行数进行了压缩。
也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。
proof
在PCA中，我们可以通过计算数据的协方差矩阵来找到主成分方向这个协方差矩阵可以被分解为\(C=V\Lambda V^{T}\)其中\(V\)是特征向量矩阵,\(\Lambda\)是特征值对角矩阵
对数据进行去中心化后\(X_c=X-\bar X\)将\(X_c进行\)SVD分解得到\(X_{c}=U\Sigma V^{T}\)代入协方差矩阵可以得到

\[C=\frac{1}{n}X_{c}^{T}X_{c}=\frac{1}{n}V\Sigma^{2}V^{T} \]

参考

[NLP] 秒懂词向量Word2vec的本质
LangChain 🦜️🔗 中文网，跟着LangChain一起学LLM/GPT开发
动手学大模型应用开发
奇异值分解(SVD)原理与在降维中的应用
GloVe: Global Vectors for Word Representation
requirements文件下载地址

posted @ 2024-04-20 21:23  zddkk  阅读(163)  评论(0)  编辑  收藏  举报