LLM学习(1)——大模型简介

1.1.1 LLM的概念

为了区分不同参数尺度的语言模型，研究界为大规模的PLM（例如，包含数百亿或数千亿个参数）创造了术语“大型语言模型”LLM。

1.1.2 LLM的能力与缩放定律

LLM的能力

涌现能力LLMs被正式定义为“在小型模型中不存在但在大型模型中出现的能力”，这是LLMs区别于以往PLM的最突出特征之一。当出现紧急能力时，它进一步引入了一个显着的特征：当规模达到一定水平时，性能明显高于随机性。以下是三种经典的涌现能力：

  1. In-context learning
    假设语言模型已经提供了自然语言指令和/或多个任务演示，它可以通过完成输入文本的单词序列来生成测试实例的预期输出，而无需额外的训练或梯度更新
  2. Instruction following
    通过指令调优，LLMs可以在不使用显式示例的情况下遵循新任务的任务指令，从而具有更高的泛化能力。
  3. Step-by-step reasoning
    LLMs可以通过利用涉及中间推理步骤的提示机制来推导出最终答案来解决例如数学或者单词任务

LLM的缩放定律

缩放可以在很大程度上提高 LLMs的模型容量

  1. KM scaling law

\[\begin{align*} &L\left( N \right) =\left( \frac{N_C}{N} \right) ^{\alpha _N},\alpha _N\sim 0.076,N_C\sim 8.8\times 10^{13}\tag{1-a} \\ &L\left( D \right) =\left( \frac{D_C}{D} \right) ^{\alpha _N},\alpha _D\sim 0.095,D_C\sim 5.4\times 10^{13}\tag{1-b} \\ &L\left( C \right) =\left( \frac{C_C}{C} \right) ^{\alpha _N},\alpha _C\sim 0.050,C_C\sim 3.1\times 10^{13}\tag{1-c} \end{align*} \]

  1. Chinchilla scaling law

\[L\left( N,D \right) =E+\frac{A}{N^{\alpha}}+\frac{B}{D^{\beta}}\tag{2-a} \]

其中\(E\)=1.69,\(A\)=406.4,\(B\)=410.7,\(\alpha=0.34\)和\(\beta\)=0.28通过优化约束\(C\approx6ND\)下的损失\(L(N,D)\)可以推导出如下最佳分配：

\[N_{opt}\left( C \right) =G\left( \frac{C}{6} \right) ^{\alpha},D_{opt}\left( C \right) =G^{-1}\left( \frac{C}{6} \right) ^b\tag{2-b}\]

以下是推导过程：

为了找到最优的\(N\)和\(D\)，我们可以通过最小化损失函数\(L(N,D)\)来解决这个问题。首先，我们需要计算\(L(N,D)\)的梯度，然后令梯度等于零，以找到损失函数的最小值点。
首先计算\(L(N,D)\)的梯度：

\[\frac{\partial L}{\partial N}=-\alpha\frac{A}{N^{\alpha+1}} \]

\[\frac{\partial L}{\partial D}=-\beta\frac{B}{D^{\beta+1}} \]

令\(\frac{\partial L}{\partial N}=0\)和\(\frac{\partial L}{\partial D}=0\)，得到：

\[\frac{A}{N^{\alpha+1}}=\frac{B}{D^{\beta+1}} \]

由于\(C\approx6ND\)，我们可以得到\(D=\frac{C}{6N}\)，将其代入上面的等式中，得到：

\[\frac{A}{N^{\alpha+1}}=\frac{B}{\left( \frac{C}{6N} \right) ^{\beta+1}} \]

化简得到：

\[N^{\alpha}=\frac{AG}{C},D^{\beta}=\frac{BG}{C} \]

因此，最优的\(N\)和\(D\)可以表示为：

\[N_{opt}(C)=G\left( \frac{C}{6} \right) ^{\alpha},D_{opt}(C)=G^{-1}\left( \frac{C}{6} \right) ^{\beta} \]

其中\(G=\left( \frac{AG}{C} \right) ^{\frac{1}{\alpha}}\)。这就是通过优化约束\(C\approx6ND\)下的损失\(L(N,D)\)推导出的最佳分配。

1.2.1 RAG的概念

图(1)

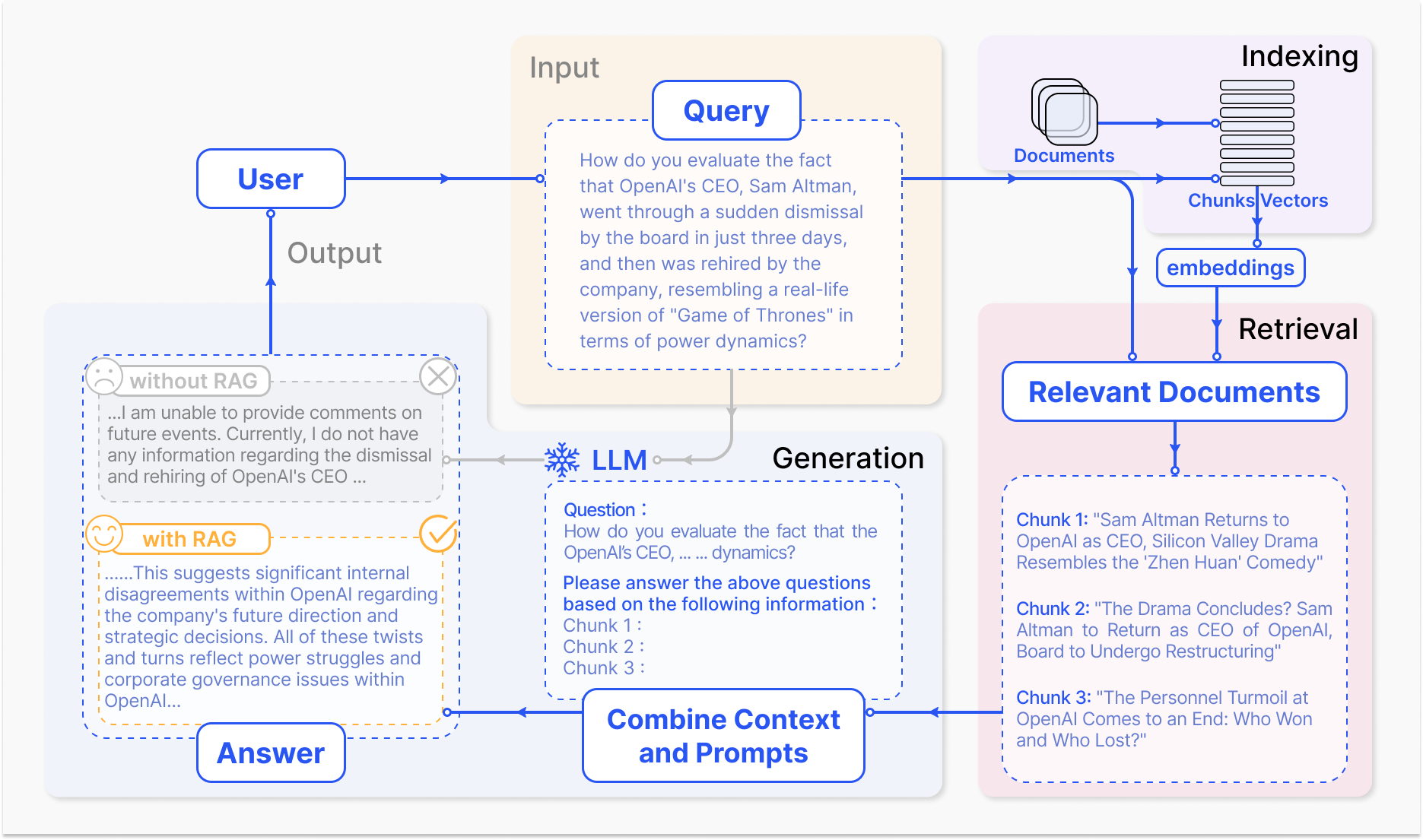
图(1)显示了RAG应用于问答的三个步骤：

  1. Indexing：文档被拆分为块，编码为向量，并且储存在向量数据库中
  2. Retrieval：根据语义的相似性检索与问题最相关的前k个块
  3. Generation：将原始问题和检索到的块一起输入以LLM生成最终答案

1.2.2 RAG的增强过程

迭代检索

迭代检索是根据初始查询和到目前为止生成的文本重复搜索知识库的过程，为 LLMs提供更全面的知识库。这种方法已被证明可以通过多次检索迭代提供额外的上下文引用来增强后续答案生成的鲁棒性。但是，它可能会受到语义不连续性和不相关信息积累的影响。

递归检索

递归检索通常用于信息检索和 NLP，以提高搜索结果的深度和相关性。该过程涉及根据从先前搜索中获得的结果迭代优化搜索查询。递归检索旨在通过反馈循环逐渐收敛到最相关的信息，从而增强搜索体验。

自适应检索

通过主动确定检索的最佳时刻和内容来完善RAG框架LLMs，从而提高信息来源的效率和相关性。

1.3.1LangChain简要介绍

LangChain 是一个开源框架,允许AI开发人员将 GPT-4 等大型语言模型(LLMs)与外部数据相结合

1.3.2 LangChain的核心组件

  1. Models (LLM Wrappers) 模型 （LLM 包装纸）
  2. Prompts 提示
  3. Chains 链
  4. Embeddings and Vector Stores 嵌入和矢量存储
  5. Agents 代理
  6. Callback 回调

环境配置

电脑配置 
处理器	AMD Ryzen 7 5800H with Radeon Graphics            3.20 GHz
机带 RAM	16.0 GB (15.9 GB 可用)
系统类型	64 位操作系统, 基于 x64 的处理器
笔和触控	没有可用于此显示器的笔或触控输入
版本	Windows 11 家庭中文版
版本	22H2
GPU      NVIDIA RTX3060
运行 
git clone git@github.com:datawhalechina/llm-universe.git

的时候出现以下错误

fatal: Could not read from remote repository.
Please make sure you have the correct access rights
and the repository exists.

原因是更新了win11之后ssh应该重新创建添加
重新添加后成功克隆

图(2)
创建虚拟环境并且激活 
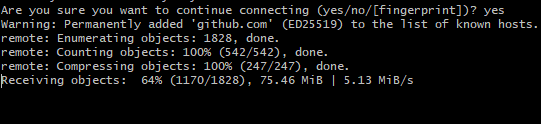
python -m venv .venv
.\.venv\Scripts\Activate.ps1

安装库文件

pip install -r requirements.txt -y

结果：

图(3)

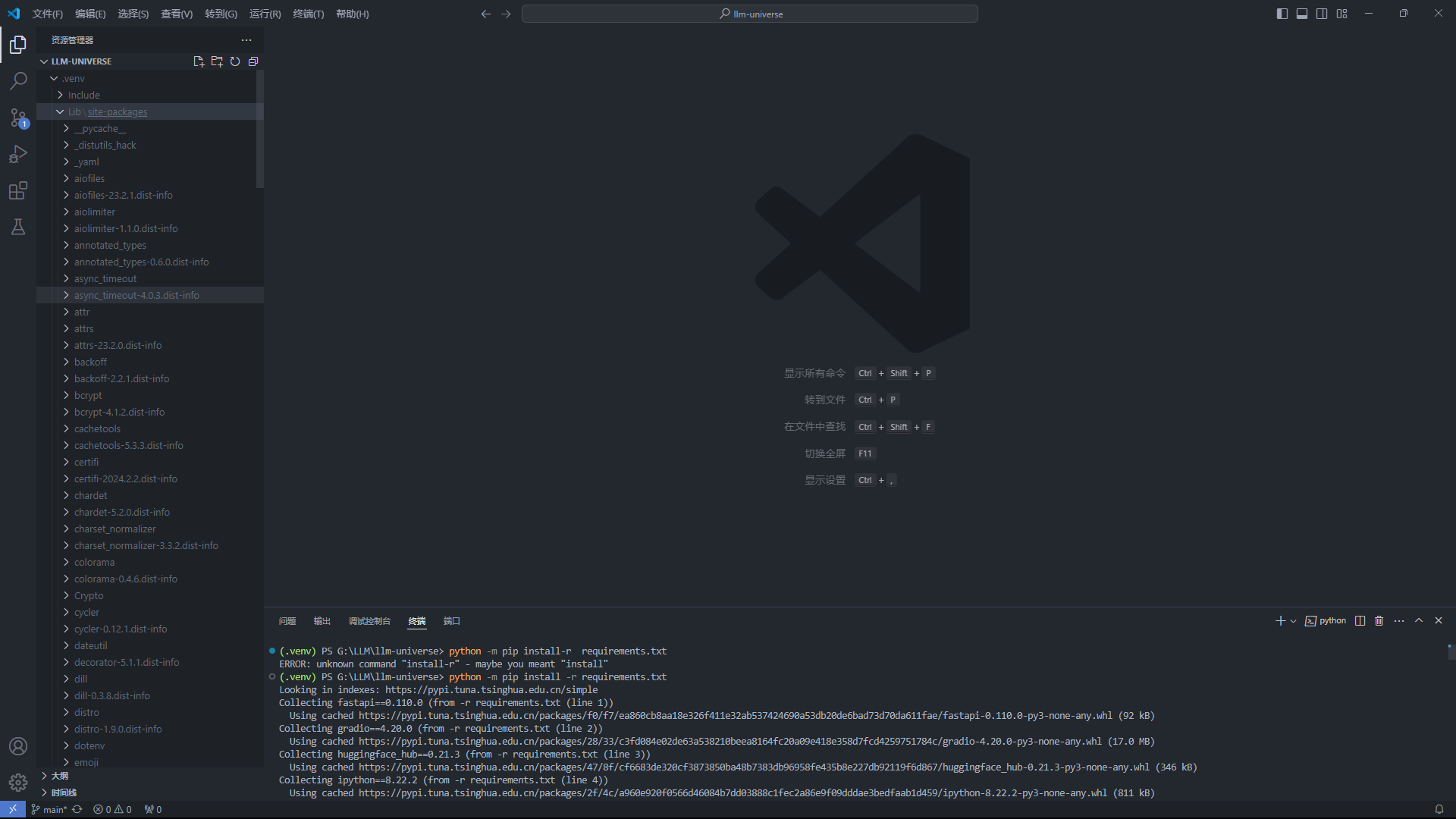
参考：

大模型RAG的迭代路径
LangChain Tutorial – How to Build a Custom-Knowledge Chatbot
动手学大模型应用开发

posted @ 2024-04-15 15:48  zddkk  阅读(150)  评论(0)  编辑  收藏  举报