强化学习基础第二讲基于模型的动态规划算法

上一讲我们将强化学习的问题纳入到马尔科夫决策过程的框架下进行解决。一个完整的已知模型的马尔科夫决策过程可以利用元组 $\left( {S,A,P,r,\gamma } \right)$ 来表示。其中 $S$ 为状态集， $A$ 为动作集， $P$ 为转移概率，也就是对应着环境和智能体的模型， $r$ 为回报函数， $\gamma$ 为折扣因子用来计算累积回报 $R$ 。累积回报公式为 $R = \sum\limits_{t = 0}^T {{\gamma ^t}} {r_t}$ ，其中 $0 \le \gamma \le 1$ ， $T$ 为有限值时，强化学习过程称为有限范围强化学习，当 $T = \infty$ 时，称为无穷范围强化学习。我们以有限范围强化学习为例进行讲解。

强化学习的目标是找到最优策略 $\pi$ 使得累积回报的期望最大。所谓策略是指状态到动作的映射 $\pi: s \to a$ ，用 $\tau$ 表示从状态 $s$ 到最终状态的一个序列 $\tau: {s_t},{s_{t + 1}} \cdots ,{s_T}$ ，则累积回报 $R(\tau)$ 是个随机变量，随机变量无法进行优化，无法当成是目标函数，采用随机变量的期望作为目标函数，即 $\int {R\left( \tau \right)} {p_\pi }\left( \tau \right)d\tau$ 作为目标函数。用公式来表示强化学习的目标为： $\mathop {\max }\limits_\pi \int {R\left( \tau \right)} {p_\pi }\left( \tau \right)d\tau$ 。强化学习的最终目标是找到最优策略为： ${\pi ^*}:s \to {u^*}$ ，我们看一下这个表达式的直观含义。

图2.1 序列决策示意图

如图2.1所示，最优策略的目标是找到决策序列 $u_0^* \to u_1^* \to \cdots u_T^*$ ，因此从广义上来讲，强化学习可以归结为序列决策问题。即找到一个决策序列，使得目标函数最优。这里的目标函数 $\int {R\left( \tau \right)} {p_\pi }\left( \tau \right)d\tau$ 是累积回报的期望值，所谓的累积回报其背后的含义是评价策略完成任务的回报，所以目标函数等价于任务。强化学习的直观目标是找到最优策略，其目的是更好地完成任务。回报函数对应着具体的任务，所以强化学习所学到的最优策略是跟具体的任务相对应的。从这个意义上来说，强化学习并不是万能的，它无法利用一个算法实现所有的任务。

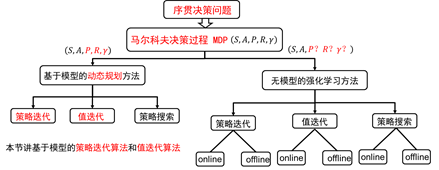
图2.2 强化学习分类

从广义上讲，强化学习是序贯决策问题。但序贯决策问题包含的内容更丰富。它不仅包含马尔科夫过程的决策，而且包括非马尔科夫过程的决策。在上一节，我们已经将强化学习纳入到马尔科夫决策过程MDP的框架之内。马尔科夫决策过程可以利用元组 $\left( {S,A,P,r,\gamma } \right)$ 来描述，根据转移概率 $P$ 是否已知，可以分为基于模型的动态规划方法和基于无模型的强化学习方法，如图2.2。两种类别都包括策略迭代算法，值迭代算法和策略搜索算法。不同的是无模型的强化学习方法每类算法又分为online和offline两种。Online和offline的具体含义，下一节会详细介绍。

基于模型的强化学习可以利用动态规划的思想来解决。顾名思义，动态规划中的动态蕴含着序列和状态的变化；规划蕴含着优化，如线性优化，二次优化或者非线性优化。利用动态规划可以解决的问题需要满足两个条件：（1）整个优化问题可以分解为多个子优化问题，子优化问题的解可以被存储和重复利用。上节已经讲过，强化学习可以利用马尔科夫决策过程来描述，利用贝尔曼最优性原理得到贝尔曼最优化方程：

$\begin{array}{l}{\upsilon ^*}\left( s \right) = \mathop {\max }\limits_a R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{\upsilon ^*}} \left( {s'} \right)\\{q^*}\left( {s,a} \right) = R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{{\max }_{a'}}{q^*}} \left( {s',a'} \right)\end{array}$ (2.1)

从方程（2.1）中可以看到，马尔科夫决策问题符合使用动态规划的两个条件，因此可以利用动态规划解决马尔科夫决策过程的问题。

贝尔曼方程（2.1）指出，动态规划的核心是找到最优值函数。那么，第一个问题是：给定一个策略 $\pi$ ，如何计算在策略 $\pi$ 下的值函数？其实上节已经讲过，此处再重复一遍：

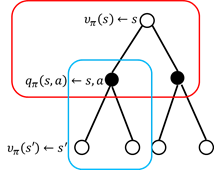
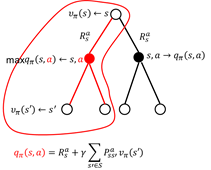
图2.3 值函数计算过程

如图2.3，红色方框内的计算公式为：

${\upsilon _\pi }\left( s \right) = \sum\limits_{a \in A} {\pi \left( {a|s} \right){q_\pi }} \left( {s,a} \right){\kern 1pt}$ (2.2)

该方程表示，在状态 $s$ 处的值函数等于采用策略 $\pi$ 时，所有状态-行为值函数的总和。蓝色方框的计算公式为状态-行为值函数的计算：

${q_\pi }\left( {s,a} \right) = R_s^a + \gamma \sum\limits_{s'} {P_{ss'}^a{\upsilon _\pi }} \left( {s'} \right){\kern 1pt}$ ${q_\pi }\left( {s,a} \right) = R_s^a + \gamma \sum\limits_{s'} {P_{ss'}^a{\upsilon _\pi }} \left( {s'} \right)$ (2.3)

该方程表示，在状态 $s$ 采用动作 $a$ 的状态值函数等于回报加上后续状态值函数。将方程（2.3）带入方程（2.2）便得到状态值函数的计算公式：

${\upsilon _\pi }\left( s \right) = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \left( {R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{\upsilon _\pi }\left( {s'} \right)} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}$ (2.4)

状态 $s$ 处的值函数 ${\upsilon _\pi }\left( s \right)$ ，可以利用后继状态的值函数 ${\upsilon _\pi }\left( {s'} \right)$ 来表示。可是有人会说，后继状态的值函数 ${\upsilon _\pi }\left( {s'} \right)$ 也是不知道的，那怎么计算当前状态的值函数？这不是自己抬起自己吗？如图2.4所示。没错，这正是bootstrapping算法(自举算法)。

2.4 自举示意图

Bootstrapping and Artificial Intelligence

如何求解（2.4）所示的方程？首先，我们从数学的角度去解释方程(2.4)。对于模型已知的强化学习算法，方程(2.4)中的 $P_{ss'}^a$ ， $\gamma$ 和 ${R_s}^a$ 都是已知数， $\pi \left( {a|s} \right)$ 为要评估的策略是指定的，也是已知值。方程（2.4）中唯一的未知数是值函数，从这个角度去理解方程（2.4）可知，方程（2.4）是关于值函数的线性方程组，其未知数的个数为状态的总数，用 $\left| S \right|$ 来表示。此处，我们使用高斯-赛德尔迭代算法进行求解。即：

${\upsilon _{k + 1}}\left( s \right) = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \left( {R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a{\upsilon _k}\left( {s'} \right)} } \right)$ (2.5)

下面我们给出策略评估算法的伪代码：

图2.5 策略评估算法

如图2.5所示为策略评估算法的伪代码。需要注意的是，在每次迭代中都需要对状态集进行一次遍历（扫描）以便评估每个状态的值函数。

接下来，我们举个策略评估的例子：

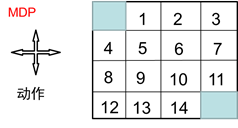
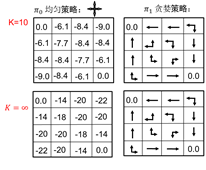
如图2.6所示为网格世界，其状态空间为： $S = \left\{ {1,2, \cdots ,14} \right\}$ ，动作空间 A={东，南，西，北}，回报函数为 $r\equiv -1$ ,需要评估的策略为均匀随机策略：π(东|⋅)= 0.25， π(南|⋅)= 0.25， π(西|⋅)=0.25， π(北|⋅)= 0.25.

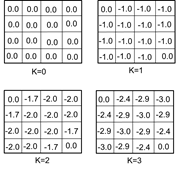
图2.6 网格世界

图2.7 值函数迭代中间图

图2.7为值函数迭代过程值函数的变化。为了进一步说明，我们举个具体地例子，如从K=1到K=2时，状态1处的值函数计算过程。

由公式2.5得到：

${\upsilon _2}\left( 1 \right){\rm{ = }}0.25{\rm{*}}\left( {{\rm{ - }}1{\rm{ - }}1} \right){\rm{ + }}0.25{\rm{*}}\left( {{\rm{ - }}1{\rm{ - }}1} \right) + 0.25{\rm{*}}\left( {{\rm{ - }}1{\rm{ - }}1} \right) + 0.25{\rm{*}}\left( {0{\rm{ - }}1} \right){\rm{ = }}0.25{\rm{*}}\left( {{\rm{ - }}7} \right){\rm{ = - }}1.75$

保留两位有效数字便是-1.7。

计算值函数的目的是利用值函数找到最优策略。第二个要解决的问题是：如何利用值函数进行策略改善，从而得到最优策略？

一个很自然的方法是当已知当前策略的值函数时，在每个状态采用贪婪策略对当前策略进行改进，即： ${\pi _{l + 1}}\left( s \right) \in \mathop {\arg {\kern 1pt} {\kern 1pt} \max }\limits_a {\kern 1pt} {\kern 1pt} {\kern 1pt} {q^{{\pi _l}}}\left( {s,a} \right)$

图2.8 贪婪策略计算

如图2.8给出了贪婪策略示意图。图中红线为最优策略选择。

图2.9 方格世界贪婪策略选取

如图2.9所示为方格世界贪婪策略的示意图。我们仍然以状态1为例得到改进的贪婪策略：

至此，我们已经给出了策略评估算法和策略改进算法。万事已具备，将策略评估算法和策略改进算合起来便组成了策略迭代算法。

图2.10 策略迭代算法

策略迭代算法包括策略评估和策略改进两个步骤。在策略评估中，给定策略，通过数值迭代算法不断计算该策略下每个状态的值函数，利用该值函数和贪婪策略得到新的策略。如此循环下去，最终得到最优策略。这是一个策略收敛的过程。

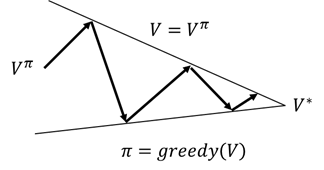
图2.11 值函数收敛

如图2.11 所示为值函数收敛过程，通过策略评估和策略改进得到最优值函数。从策略迭代的伪代码我们看到，进行策略改进之前需要得到收敛的值函数。值函数的收敛往往需要很多次迭代，现在的问题是进行策略改进之前一定要等到策略值函数收敛吗？

对于这个问题，我们还是先看一个例子：

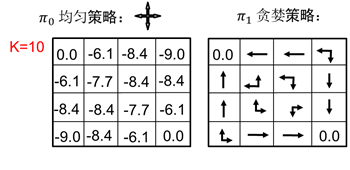
图2.12 策略改进

如图2.12所示，策略评估迭代10次和迭代无穷次所得到的贪婪策略是一样的。因此，对于上面的问题，我们的回答是不一定等到策略评估算法完全收敛。如果我们在进行一次评估之后就进行策略改善，则称为值函数迭代算法。

值函数迭代算法的伪代码为：

图2.13 值函数迭代算法

如图2.13为值函数迭代算法。需要注意的是在每次迭代过程，需要对状态空间进行一次扫描，同时在每个状态对动作空间进行扫描以便得到贪婪的策略。

值函数迭代是动态规划算法最一般的计算框架，我们阐述最优控制理论与值函数迭代之间的联系。解决最优控制的问题往往有三种思路：变分法原理、庞特里亚金最大值原理和动态规划的方法。三种方法各有优缺点。

基于变分法的方法是最早的方法，其局限性是无法求解带有约束的优化问题。基于庞特里亚金最大值原理的方法在变分法基础上进行发展，可以解决带约束的优化问题。相比于这两种经典的方法，动态规划的方法相对独立，主要是利用贝尔曼最优性原理。

对于一个连续系统，往往有一组状态方程来描述：

${\rm{\dot X = }}f\left( {t,X,U} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} X\left( {{t_0}} \right) = {X_0}$ (2.6)

性能指标往往由积分给出：

$J\left[ {x\left( {{t_0}} \right),{t_0}} \right] = \phi \left[ {X\left( {{t_f}} \right),{t_f}} \right] + \int_{{t_0}}^{{t_f}} {L\left( {x\left( t \right),u\left( t \right),t} \right)}$ (2.7)

最优控制的问题是：

$V\left( {X,t} \right) = \mathop {\min }\limits_{u \in \Omega } \left\{ {\phi \left[ {X\left( {{t_f}} \right),{t_f}} \right] + \int_{{t_0}}^{{t_f}} {L\left( {x\left( t \right),u\left( t \right),t} \right)} } \right\}$ (2.8)

由贝尔曼最优性原理得到哈密尔顿-雅克比-贝尔曼方程：

$- {{\partial V} \over {\partial t}} = \mathop {\min }\limits_{u\left( t \right) \in U} \left\{ {L\left( {x\left( t \right),u\left( t \right),t} \right) + {{\partial V} \over {\partial {X^T}}}f\left[ {x\left( t \right),u\left( t \right),t} \right]} \right\}$ (2.9)

方程(2.9)是一个偏微分方程，一般不存在解析解。对于偏微分方程(2.9)，有三种解决思路：（1）将值函数进行离散，求解方程（2.9）的数值解，然后利用贪婪策略得到最优控制。这对应于求解微分方程的数值求解方法。（2）第二个思路是利用变分法，将微分方程转化成变分代数方程，在标称轨迹展开，得到微分动态规划DDP。（3）利用函数逼近理论，对方程中的回报函数和控制函数进行函数逼近，利用优化方法得到逼近系数，这类方法称为伪谱的方法。

前两种方法都是以值函数为中心，其思路与值函数迭代类似，我们在此介绍前两种方法。

HJB方程的数值算法：

图2.14 平面移动机器人移动规划 [1]

如图2.14为平面移动机器人的移动规划部分的代码，从代码中我们看到，如图2.14红色框内节点处的值进行计算时选取的也是最小值函数。

第二个思路是采用变分法。下面我们给出DDP方法的具体推导公式和伪代码：

由贝尔曼最优性原理得：

$\begin{gathered} V\left( {X,t} \right) = \mathop {\min }\limits_{u \in \Omega } \left\{ {\phi \left[ {X\left( {{t_f}} \right),{t_f}} \right] + \int_{{t_0}}^{{t_f}} {L\left( {x\left( t \right),u\left( t \right),t} \right)dt} } \right\} \hfill \\ {\text{ = }}\mathop {\min }\limits_{u \in \Omega } \left\{ {\int_{{t_0}}^{{t_0} + dt} {L\left( {x\left( \tau \right),u\left( \tau \right),\tau } \right)d\tau + V\left( {X + \Delta X,t + dt} \right)} } \right\} \hfill \\ \end{gathered}$ (2.10)

假设： $\begin{gathered} {x_{k + 1}} = f\left( {{x_k},{u_k}} \right) \hfill \\ {V_k} = \mathop {\min }\limits_u \left[ {l\left( {{x_k},{u_k}} \right) + {V_{k + 1}}\left( {{x_{k + 1}}} \right)} \right] \hfill \\ \end{gathered}$ 令 $Q\left( {\delta x,\delta u} \right) = V\left( {x + \delta x} \right) - V\left( x \right)$ ，则 $Q$

在标称轨迹 $\left( {{x_k},{u_k}} \right)$ 展开： $\begin{gathered} Q\left( {\delta x,\delta u} \right) = V\left( {x + \delta x} \right) - V\left( x \right) \hfill \\ {\text{ = }}l\left( {{x_k} + \delta {x_k},{u_k} + \delta {u_k}} \right) + {V_{k + 1}}\left( {{x_{k + 1}} + \delta {x_{k + 1}}} \right) - \left( {l\left( {{x_k},{u_k}} \right) + {V_{k + 1}}\left( {{x_{k + 1}}} \right)} \right) \hfill \\ \approx \delta x_k^T{l_{{x_k}}} + \delta u_k^T{l_{{u_k}}} + \frac{1}{2}\left( {\delta x_k^T{l_{x{x_k}}}\delta {x_k} + 2\delta x_k^T{l_{x{u_k}}}\delta {u_k} + \delta u_k^T{l_{u{u_k}}}\delta {u_k}} \right) + \delta x_{k + 1}^T{V_{{x_{k + 1}}}} + \frac{1}{2}\delta x_{k + 1}^T{V_{x{x_{k + 1}}}}\delta {x_{k + 1}} \hfill \\ \end{gathered}$ (2.11)

又 ${x_{k + 1}} = f\left( {{x_k},{u_k}} \right)$ ，得到： $\delta {x_{k + 1}} = \delta f\left( {{x_k},{u_k}} \right) = {f_{{x_k}}}\delta {x_k} + {f_{{u_k}}}\delta {u_k} + \frac{1}{2}\left( {\delta x_k^T{f_{x{x_k}}}\delta x + 2\delta x_k^T{f_{x{u_k}}}\delta {u_k} + \delta u_k^T{f_{u{u_k}}}\delta u} \right)$ （2.12）将(2.12)带入到（2.11）可以得到：

$Q\left( {\delta x,\delta u} \right) = \frac{1}{2}\left[ {\delta {u^T}{Q_{uu}}\delta u + \left( {\delta {u^T}{Q_{ux}}\delta x + \delta {x^T}{Q_{xu}}\delta u} \right) + Q_u^T\delta u + \delta {u^T}{Q_u} + \delta {x^T}{Q_{xx}}\delta x + \delta {x^T}{Q_x} + Q_x^T\delta x} \right]$
（2.13）

其中：

$\begin{gathered} {Q_x} = {l_{{x_k}}} + f_{{x_k}}^T{V_{{x_{k + 1}}}} \hfill \\ {Q_u} = {l_{{u_k}}} + f_{{u_k}}^T{V_{{x_{k + 1}}}} \hfill \\ {Q_{xx}} = {l_{x{x_k}}} + f_{{x_k}}^T{V_{x{x_k}}}{f_{{x_k}}} + {V_{{x_{k + 1}}}}{f_{{x_k}{x_k}}} \hfill \\ {Q_{uu}} = {l_{u{u_k}}} + f_{{u_k}}^T{V_{x{x_{k + 1}}}}{f_{{u_k}}} + {V_{{x_{k + 1}}}}{f_{{u_k}{u_k}}} \hfill \\ {Q_{ux}} = {l_{u{x_k}}} + f_{{u_k}}^T{V_{x{x_{k + 1}}}}{f_{{x_k}}} + {V_{{x_{k + 1}}}}{f_{u{x_k}}} \hfill \\ \end{gathered}$ （2.14）

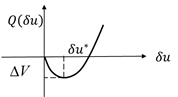
将（2.13）视为 $\delta u$ 的函数，则 $Q\left( {\delta x,\delta u} \right)$ 是 $\delta u$ 的二次函数。

图2.15 值函数变分函数

如图2.15所示， $\delta {u^*} = \mathop {\arg \min }\limits_{\delta u} Q\left( {\delta x,\delta u} \right) = - Q_{uu}^{ - 1}\left( {{Q_u} + {Q_{ux}}\delta x} \right)$ 。我们令

$k = - Q_{uu}^{ - 1}{Q_u},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K = - Q_{uu}^{ - 1}{Q_{ux}}$ （2.15）

则 $\delta {u^*} = \mathop {\arg \min }\limits_{\delta u} Q\left( {\delta x,\delta u} \right) = k + K\delta x$

$\begin{gathered} \Delta V = - \frac{1}{2}{Q_u}Q_{uu}^{ - 1}{Q_u} \hfill \\ {V_{{x_k}}} = {Q_x} - {Q_u}Q_{uu}^{ - 1}{Q_{ux}} \hfill \\ {V_{x{x_k}}} = {Q_{xx}} - {Q_{xu}}Q_{uu}^{ - 1}{Q_{ux}} \hfill \\ \end{gathered}$ （2.16）

微分动态规划的伪代码为：

1. 前向迭代：给定初始控制序列 ${\bar u_k}$ ，正向迭代计算标称轨迹

${\bar x_{k + 1}} = f\left( {{{\bar x}_k},{{\bar u}_k}} \right),{l_{{x_k}}},{f_{{u_k}}},{l_{x{x_k}}},{l_{x{u_k}}},{l_{u{u_k}}}$
2. 反向迭代：由代价函数边界条件 ${V_{{x_N}}},{V_{x{x_N}}}$ ，反向迭代计算（2.14），（2.15）和（2.16）得到贪婪策略 $\delta {u^*}$

3. 正向迭代新的控制序列：

$\begin{gathered} {x_1} = \bar x\left( 1 \right) \hfill \\ {u_k} = {{\bar u}_k} + {k_k} + {K_k}\left( {{x_k} - {{\bar x}_k}} \right) \hfill \\ {x_{k + 1}} = f\left( {{x_k},{u_k}} \right) \hfill \\ \end{gathered}$

从第二步反向迭代计算贪婪策略的过程我们可以看到，贪婪策略通过最小化值函数得到。

posted @ 2017-12-01 14:31 小时候挺菜阅读(1814) 评论(0) 编辑收藏举报

刷新页面返回顶部

强化学习基础 第二讲 基于模型的动态规划算法

公告

强化学习基础第二讲基于模型的动态规划算法