计算机系统--补码，原码及反码

无符号数的编码

　　假设有一个w位的无符号整数，我们可以将位向量写成[x_w-1 , x_w-2 , … , x₂ , x₁ , x₀]。其中每个x_i都取值为0或1，我们用一个函数B2U_w（Binary to unsigned，长度为w）来表示：

　　

　　函数B2U将一个长度为w的0、1串映射到非负整数：

　　

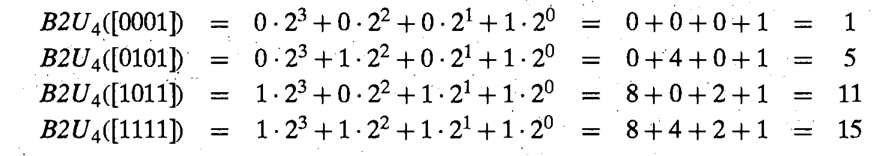
　　对于一个无符号编码的数，由 w 位的二进制序列构成，那么它的最小值，即所有位都为 0 ,用位向量表示即：000......000。

　　　　UMin_w = 0

　　最大值即所有位都为 1，即：111......111

 　　　　UMax_w = 2^w - 1 

补码编码 

　　对于许多应用，我们还希望表示负数值，最常见的有符号数的计算机表示方式就是补码，在补码中，最高有效位为符号位

　　我们用B2T_w来（Binary to Two's-conplement，长度为w）来表示：

　　

　　

 

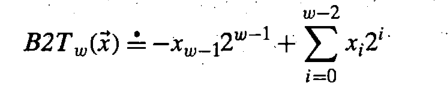
 　　当最高位为1，其余为全部是 0 的时候，即 1000......000，表示补码格式的最小值：

　　　　TMin_w = -2^w-1 

　     当最高位为 0，其余为全部是 1 时，即 0111......111，表示补码格式的最大值：

　　　　TMax_w = 2^w-1-1

 反码和原码

　　反码：除了最高有效位的权是-(2^w-1-1)，而不是-2^w-1其余的和补码表示方式一样

　　　　

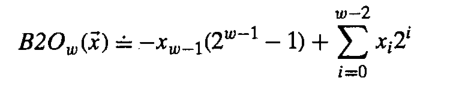
　　原码：最高有效位是符号位，用来确定剩下的位是取负还是正

　　　

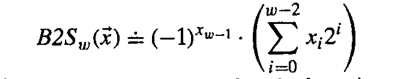
　　无符号数补码 = 原码取反 + 1

　　有符号数补码 = 除符号位原码取反 + 1

　　对于负整数，原码和补码互相转换的简便方法：从数的右边往左开始数,遇到“0”不理它,直到遇到第一个“1”为止,以后的每一位数取反即是它的原码或补码,符号位不变,还是“1”（补码的补码是原码）。

 

参考 ：https://www.cnblogs.com/ysocean/p/7531660.html