《数据结构与算法之美》 <07>队列:队列在线程池等有限资源池中的应用?
我们知道,CPU 资源是有限的,任务的处理速度与线程个数并不是线性正相关。相反,过多的线程反而会导致 CPU 频繁切换,处理性能下降。所以,线程池的大小一般都是综合考虑要处理任务的特点和硬件环境,来事先设置的。
当我们向固定大小的线程池中请求一个线程时,如果线程池中没有空闲资源了,这个时候线程池如何处理这个请求?是拒绝请求还是排队请求?各种处理策略又是怎么实现的呢?
实际上,这些问题并不复杂,其底层的数据结构就是我们今天要学的内容,队列(queue)。
如何理解“队列”?
队列这个概念非常好理解。你可以把它想象成排队买票,先来的先买,后来的人只能站末尾,不允许插队。先进者先出,这就是典型的“队列”。
我们知道,栈只支持两个基本操作:入栈 push()和出栈 pop()。队列跟栈非常相似,支持的操作也很有限,最基本的操作也是两个:入队 enqueue(),放一个数据到队列尾部;出队 dequeue(),从队列头部取一个元素。
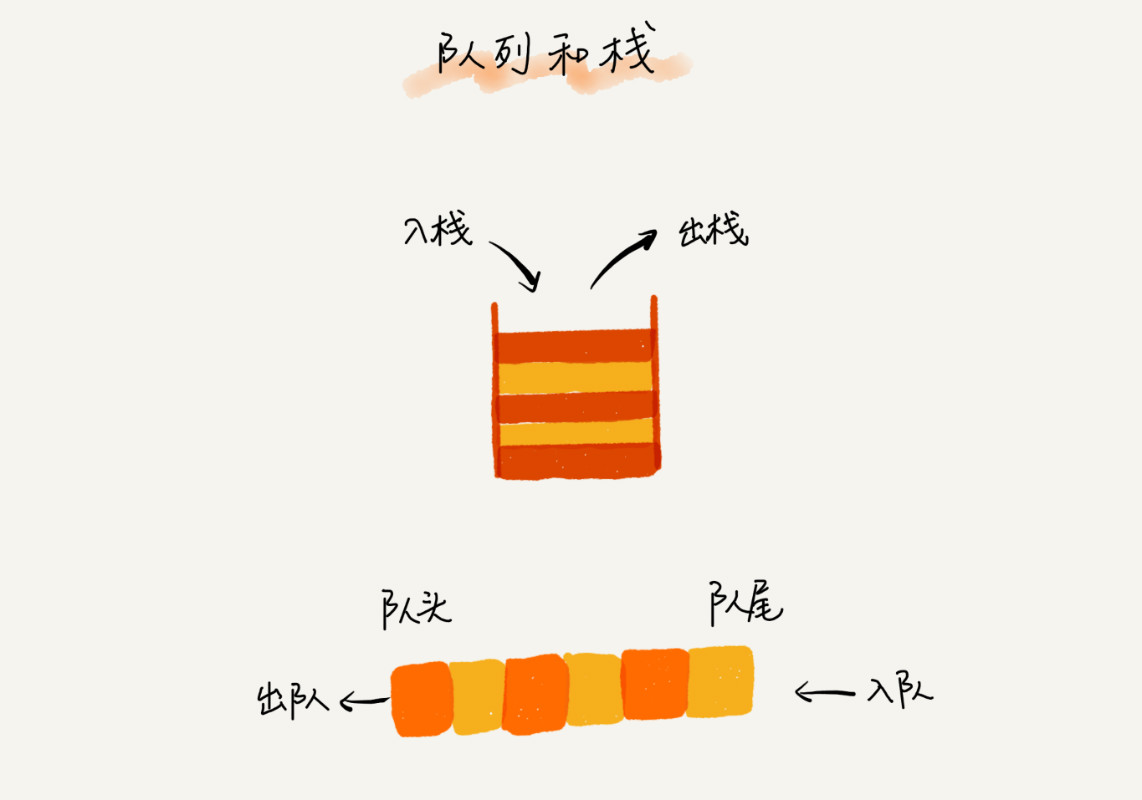
所以,队列跟栈一样,也是一种操作受限的线性表数据结构。
队列的概念很好理解,基本操作也很容易掌握。作为一种非常基础的数据结构,队列的应用也非常广泛,特别是一些具有某些额外特性的队列,比如循环队列、阻塞队列、并发队列。它们在很多偏底层系统、框架、中间件的开发中,起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存,都用到了循环并发队列;Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。
顺序队列和链式队列
我们知道了,队列跟栈一样,也是一种抽象的数据结构。它具有先进先出的特性,支持在队尾插入元素,在队头删除元素,那究竟该如何实现一个队列呢?
跟栈一样,队列可以用数组来实现,也可以用链表来实现。用数组实现的栈叫作顺序栈,用链表实现的栈叫作链式栈。同样,用数组实现的队列叫作顺序队列,用链表实现的队列叫作链式队列。
我们先来看下基于数组的实现方法。我用 Java 语言实现了一下,不过并不包含 Java 语言的高级语法,而且我做了比较详细的注释,你应该可以看懂。
// 用数组实现的队列 public class ArrayQueue { // 数组:items,数组大小:n private String[] items; private int n = 0; // head表示队头下标,tail表示队尾下标 private int head = 0; private int tail = 0; // 申请一个大小为capacity的数组 public ArrayQueue(int capacity) { items = new String[capacity]; n = capacity; } // 入队 public boolean enqueue(String item) { // 如果tail == n 表示队列已经满了 if (tail == n) return false; items[tail] = item; ++tail; return true; } // 出队 public String dequeue() { // 如果head == tail 表示队列为空 if (head == tail) return null; // 为了让其他语言的同学看的更加明确,把--操作放到单独一行来写了 String ret = items[head]; ++head; return ret; } }
比起栈的数组实现,队列的数组实现稍微有点儿复杂,但是没关系。我稍微解释一下实现思路,你很容易就能明白了。
对于栈来说,我们只需要一个栈顶指针就可以了。但是队列需要两个指针:一个是 head 指针,指向队头;一个是 tail 指针,指向队尾。
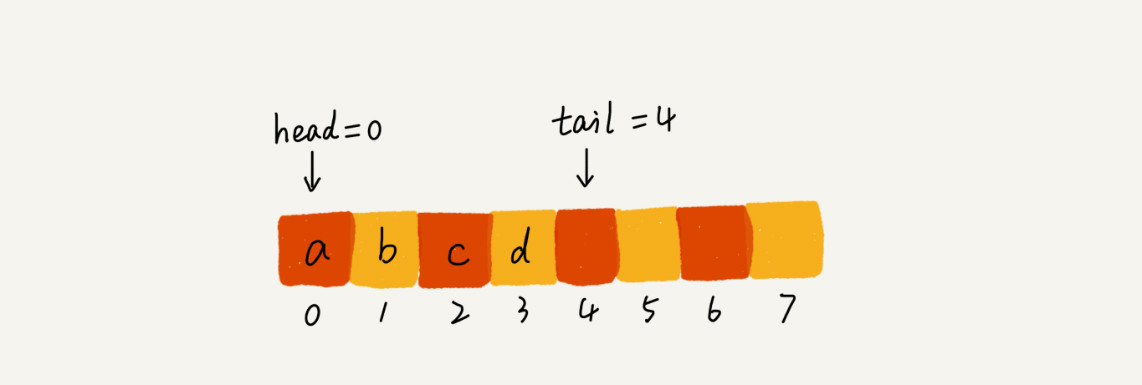
你可以结合下面这幅图来理解。当 a、b、c、d 依次入队之后,队列中的 head 指针指向下标为 0 的位置,tail 指针指向下标为 4 的位置。
当我们调用两次出队操作之后,队列中 head 指针指向下标为 2 的位置,tail 指针仍然指向下标为 4 的位置。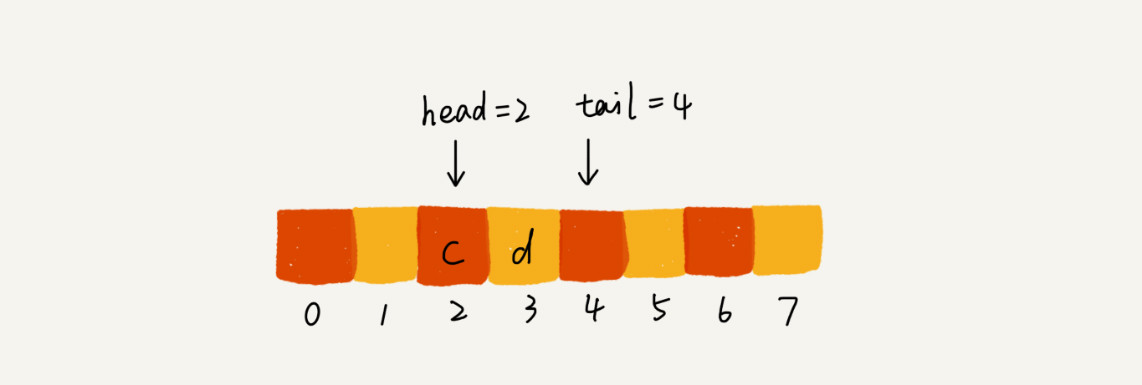
你肯定已经发现了,随着不停地进行入队、出队操作,head 和 tail 都会持续往后移动。当 tail 移动到最右边,即使数组中还有空闲空间,也无法继续往队列中添加数据了。这个问题该如何解决呢?
你是否还记得,在数组那一节,我们也遇到过类似的问题,就是数组的删除操作会导致数组中的数据不连续。你还记得我们当时是怎么解决的吗?对,用数据搬移!但是,每次进行出队操作都相当于删除数组下标为 0 的数据,要搬移整个队列中的数据,这样出队操作的时间复杂度就会从原来的 O(1) 变为 O(n)。能不能优化一下呢?
实际上,我们在出队时可以不用搬移数据。如果没有空闲空间了,我们只需要在入队时,再集中触发一次数据的搬移操作。借助这个思想,出队函数 dequeue() 保持不变,我们稍加改造一下入队函数 enqueue() 的实现,就可以轻松解决刚才的问题了。下面是具体的代码:
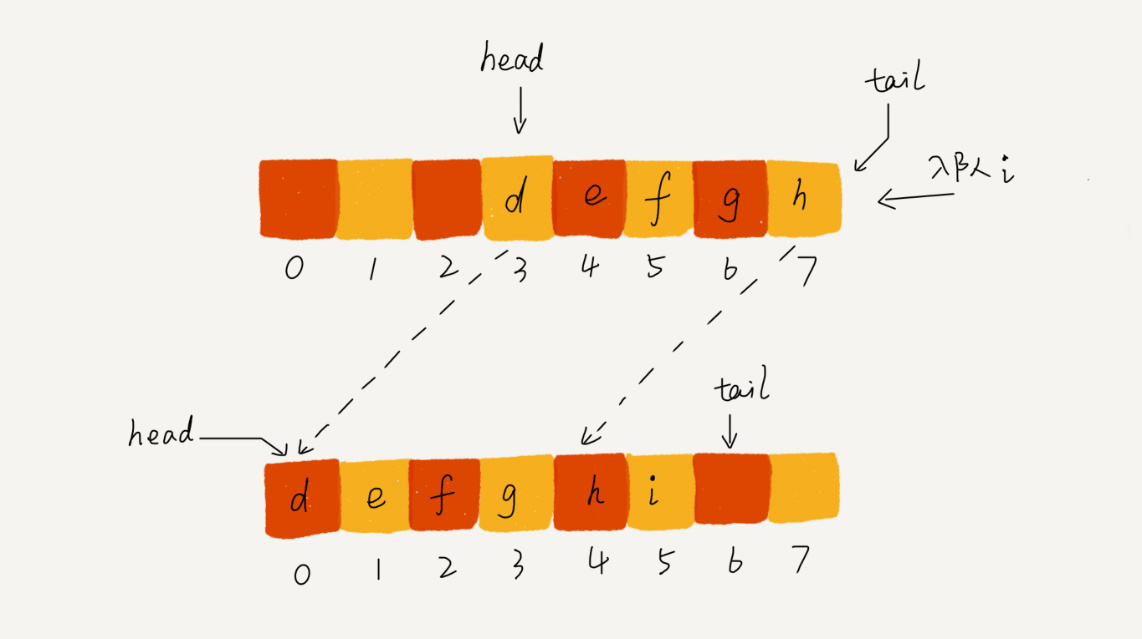
这种实现思路中,出队操作的时间复杂度仍然是 O(1),但入队操作的时间复杂度还是 O(1) 吗?你可以用我们第 3 节、第 4 节讲的算法复杂度分析方法,自己试着分析一下。
接下来,我们再来看下基于链表的队列实现方法。
基于链表的实现,我们同样需要两个指针:head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。如图所示,入队时,tail->next= new_node, tail = tail->next;出队时,head = head->next。我将具体的代码放到 GitHub 上,你可以自己试着实现一下,然后再去 GitHub 上跟我实现的代码对比下,看写得对不对。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号