JavaScript篇(一)二叉树的插入 (附:可视化)
一、二叉树概念
二叉树(binary tree)是一颗树,其中每个节点都不能有多于两个的儿子。
字节一面,第一道就是二叉树的插入,在这里其实是对于一个二叉查找树的插入。
使二叉树成为二叉查找树的性质是,对于树中的每个节点X,它的左子树中所有项的值小于X中的项目,而它的右子树所有的项的值大于X中的项。
如下图,两颗都是二叉树,左边的树是查找树,右边的树则不是。右边的树在其项为6的节点(该节点正好是根节点)的左子树中,有一个节点的项是7。

接下来我们要实现二叉树的插入:
eg: 对于[ 2, 5, 4, 1, 3, 6] =>
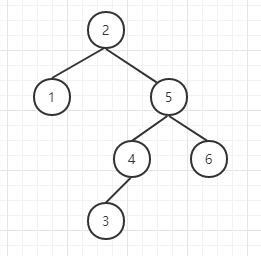
二、实现思路
1.实例化node节点
若根节点为空,便将newNode赋给root节点;
若根节点存在,则插入新节点。
2.插入左子树或右子树
1) 如果newNode小于node
1.如果node.left(左孩子)为空,newNode赋给node.left
2.否则再次比较newNode < node.left
2) 如果newNode大于node
1.如果node.right(右孩子)为空,newNode赋给node.right
2.否则再次比较newNode> node.right
三、代码实现
1 function BinaryTree(){ 2 // 定义节点 3 var Node = function(key){ 4 this.key = key; 5 this.left = null; 6 this.right = null; 7 } 8 // 初始化根节点 9 var root = null; 10 // 插入节点 11 this.insert = function(key){ 12 // 实例化node节点 13 var newNode = new Node(key); 14 // 根节点为空,便将newNode赋给root节点 15 if (root === null) { 16 root = newNode; 17 } else { 18 // 根节点存在,插入新节点 19 insertNode(root, newNode); 20 }; 21 } 22 // 插入节点(中序遍历) 23 var insertNode = function(node, newNode){ 24 // node 当前节点 25 // newNode 新节点 26 // 若newNode小于node,则插入到node的左侧 27 if(newNode.key < node.key){ 28 // 若node的左孩子为空,则插入为node的左孩子 29 if(node.left === null){ 30 node.left = newNode; 31 } else { 32 // 若node的左孩子不为空,则继续去和node的左孩子比较进行插入 33 insertNode(node.left, newNode); 34 } 35 }else { 36 if(node.right === null){ 37 node.right = newNode; 38 }else{ 39 insertNode(node.right, newNode); 40 } 41 } 42 } 43 }
var nodes = [2, 5, 4, 1, 3, 6]; var binaryTree = new BinaryTree(); // 将数组中的每个元素插入到二叉树中 nodes.forEach(function(key){ binaryTree.insert(key); })
附:可视化二叉树排序,更好去理解!(转至:https://www.imooc.com/notepad/1fb575)

<!DOCTYPE html>
<html>
<title>二叉排序树</title>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=UTF-8" />
</head>
<body >
<canvas id="canvas" width="1366" height="768" ></canvas>
</body>
</html>
<script type="text/javascript">
//二叉算法函数
function BinaryTree(){
//node 节点函数
var Node=function(key){
this.key=key;
this.left=null;
this.right=null;
this.x = 0;//图形绘制坐标
this.y = 0;//图形绘制坐标
};
/**二叉树可视图形描述**/
this.graphical = [];//图形数组
this.lrMove = 100;//左右偏移量
this.udMove = 100;//上下偏移量
/**==================**/
//定义根节点
var root=null;
//插入节点 循环递归函数 左右分插
this.insertNode=function(node,newNode){
if(newNode.key < node.key){
if(node.left===null){
var x = node.x;
var y = node.y;
newNode.x = (x -= this.udMove);
newNode.y = (y += this.lrMove);
node.left=newNode;
}else{
this.insertNode(node.left,newNode);
}
}else{
if(node.right===null){
var x = node.x;
var y = node.y;
newNode.x = (x += this.udMove);
newNode.y = (y += this.lrMove);
node.right=newNode;
}else{
this.insertNode(node.right,newNode);
}
}
};
//入口程序
this.insert=function(key){
var newNode= new Node(key);
if(root===null){
root=newNode;
root.x = 500;
root.y = 100;
this.graphical.push(root);
}else{
this.insertNode(root,newNode);
}
};
var inOrdertraverseNode = function(node,callback){
if(node !== null){
inOrdertraverseNode(node.left,callback);
callback(node.key);
inOrdertraverseNode(node.right,callback);
}
}
this.inOrdertraverse = function(callback){
inOrdertraverseNode(root,callback);
}
}
var nodes=[8,3,10,1,6,14,4,15,12,13];
var binaryTree=new BinaryTree;
for(var i = 0 ; i < nodes.length ; i++){
binaryTree.insert(nodes[i]);
}
var callback = function(key){
console.log(key)
}
binaryTree.inOrdertraverse(callback);
/*=====================================================开始绘制================================*/
var canvas = document.getElementById("canvas");
var context = canvas.getContext('2d'); //获取对应的2D对象(画笔)
function draw(key,x,y){
this.counter = 0;
this.render = function(c){
c.fillStyle = "hsl("+ this.counter +", 100%, 50%)";
c.strokeStyle = '#fff'; //设置笔触的颜色
c.font = "bold 40px '字体','字体','微软雅黑','宋体'"; //设置字体
c.textBaseline = 'hanging'; //在绘制文本时使用的当前文本基线
c.fillText(key ,x ,y);
}
this.update = function(){
this.counter += 5;
}
}
var fontCavaseArr = [];
function init() {
loop();//绘制文字
setInterval(run, 1000/30);
}
function run(x,y){
context.fillStyle = "rgba(0,0,0,0.1)";
context.fillRect(0,0,1366,768); //绘制 1366*768 像素的已填充矩形:
for (i=0; i<fontCavaseArr.length; i++) {
var particle = fontCavaseArr[i];
particle.render(context);
particle.update();
}
gLine();//绘制线条
}
function loop(){
font(binaryTree.graphical[0]);
}
function font(obj){
if(obj.key != null && obj.key != undefined){
var drawFont = new draw(obj.key,obj.x,obj.y);
fontCavaseArr.push(drawFont);
}
if(obj.left != null && obj.left != undefined){
var drawFont = new draw(obj.left.key,obj.left.x,obj.left.y);
fontCavaseArr.push(drawFont);
font(obj.left);
}
if(obj.right != null && obj.right != undefined){
var drawFont = new draw(obj.right.key,obj.right.x,obj.right.y);
fontCavaseArr.push(drawFont);
font(obj.right);
}
}
function gLine(){
line(binaryTree.graphical[0]);
}
function line(obj){
context.lineJoin="round";
context.lineCap="butt";
context.beginPath();
if(obj.left != null && obj.left != undefined){
context.moveTo(obj.x+20,obj.y+20);
context.lineTo(obj.left.x+20,obj.left.y+20);
context.stroke();
context.closePath();
line(obj.left);
}
if(obj.right != null && obj.right != undefined){
context.moveTo(obj.x+20,obj.y+20);
context.lineTo(obj.right.x+20,obj.right.y+20);
context.stroke();
context.closePath();
line(obj.right);
}
}
init();
</script>



 浙公网安备 33010602011771号
浙公网安备 33010602011771号