P3676 小清新数据结构题

P3676 小清新数据结构题

\[\sum_{u=1}^{n}\left(\sum_{v\in subtree(u)}A_v\right)^2\\ \]

后面那个东西就是子树内两两权值乘积之和。

直接维护平方必然不行，都是维护一次然后搞一些操作间接维护的。

构造一个函数

\[S=\sum A_i\\ C(rt)=\sum_{u=1}^{n}A_u\operatorname{dis}(rt,u)\\ \sum_{u=1}^{n}\sum_{v\in subtree(u)}A_v = \sum_{u=1}^{n}A_u(\operatorname{dis}(rt,u)+1)=C(rt)+S\\ \]

这个是可以维护的，修改查询都可以 \(O(\log n)\)

\(S*(C(rt)+S)\) 会计算到每一颗子树内每一个结点和所有结点权值乘积。

多算的是跨过每一条边的两颗子树内两两结点点权乘积，设为 \(D\) 。

可以发现修改一个点的点权对于 \(D\) 的贡献就是 \(\Delta\times C(x)\) ，初始值可以直接 \(O(n)\) 算。

\[ANS=S(C(rt)+S)-D \]

我是真的太逊了啊，不知道为啥你们都能理解 \(C(x)\) 的计算。

维护：

\[R_1(u)=\sum_{v\in subtree(u)}A_i\operatorname{dis}(u,v)\\ R_2(u)=\sum_{v\in subtree(u)}A_i\operatorname{dis}(vt_u,v)\\ R_3(u)=\sum_{v\in subtree(u)}A_i\\ \text{*注：vt是分治树上的父亲,subtree全针对分治树} \]

那么

\[C(rt)=R_1(rt)+\sum_{u\in vt_{rt}} R_1(vt_u)-R_2(u)+(R_3(vt_u)-R_3(u))\times \operatorname{dis}(vt_u,rt) \]

实现的时候判断 \(vt_u\) 是否存在即可，只有 \(vt_u\) 存在才加后面那个贡献。

诶诶诶？我 悟 了！确实很好理解啊，怎么之前一直觉得很难理解呢？？？

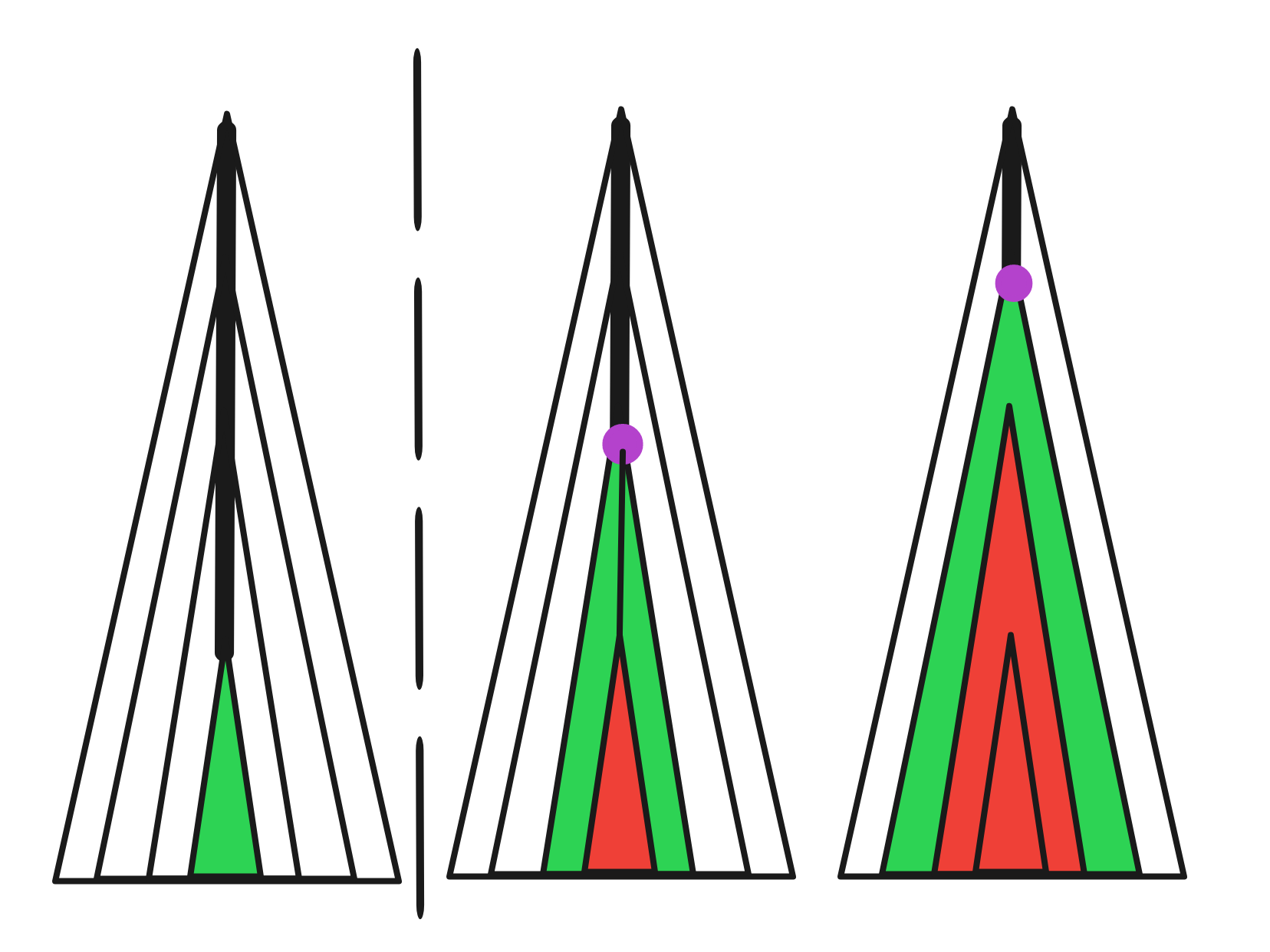
我过了一年终于理解了/ll。这里放一张自己画的图，应该很有帮助（以这题为例）：

可以看到图中分成了两部分画，所有 \(vt\) 是黑色中轴上的点，\(rt\) 是最下面那个子树的根（三角形代表子树）。

第一部分：\(R_1(rt)\) ，就是它子树内的点对它的贡献。

第二部分 \(\sum R_1(vt_u)-R_2(u)+(R_3(vt_u)-R_3(u))\times \operatorname{dis}(vt_u,rt)\) ，是子树外的部分。我们每次让绿色部分的点走到紫色结点，然后从紫色结点往下走到 \(rt\) 就能完成统计答案的任务了。

绿色部分走到紫色结点的贡献就是紫色结点子树内对它的贡献，减去红色部分对它的贡献。

悟了之后，写完过了编译就AC了，真舒服。

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define mkp(x,y) make_pair(x,y)
#define pb(x) push_back(x)
#define sz(v) (int)v.size()
typedef long long LL;
typedef double db;
template<class T>bool ckmax(T&x,T y){return x<y?x=y,1:0;}
template<class T>bool ckmin(T&x,T y){return x>y?x=y,1:0;}
#define rep(i,x,y) for(int i=x,i##end=y;i<=i##end;++i)
#define per(i,x,y) for(int i=x,i##end=y;i>=i##end;--i)
inline int read(){
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=0;ch=getchar();}
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	return f?x:-x;
}

const int N=200005;
int n,q,a[N],rt;
LL S,D,R1[N],R2[N],R3[N],sum[N];
int fa[N],top[N],son[N],dep[N],siz[N];
int hed[N],et;
struct edge{int nx,to;}e[N<<1];
void adde(int u,int v){e[++et].nx=hed[u],e[et].to=v,hed[u]=et;}

namespace Tree{
void dfs1(int u,int ft){
	siz[u]=1,dep[u]=dep[ft]+1,sum[u]=a[u];
	for(int i=hed[u];i;i=e[i].nx){
		int v=e[i].to;if(v==ft)continue;
		fa[v]=u,dfs1(v,u),siz[u]+=siz[v],sum[u]+=sum[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
	D+=sum[u]*(S-sum[u]);
}
void dfs2(int u,int tp){
	top[u]=tp;
	if(son[u])dfs2(son[u],tp);
	for(int i=hed[u];i;i=e[i].nx){
		int v=e[i].to;
		if(v!=fa[u]&&v!=son[u])dfs2(v,v);
	}
}
int LCA(int x,int y){
	while(top[x]!=top[y])dep[top[x]]>dep[top[y]]?x=fa[top[x]]:y=fa[top[y]];
	return dep[x]<dep[y]?x:y;
}
int dis(int x,int y){return dep[x]+dep[y]-(dep[LCA(x,y)]<<1);}
}
using Tree::LCA;
using Tree::dis;

namespace DFZ{
int siz[N],mx[N],tsiz,vt[N];
bool used[N];
void getrt(int u,int ft){
	siz[u]=1,mx[u]=0;
	for(int i=hed[u];i;i=e[i].nx){
		int v=e[i].to;if(v==ft||used[v])continue;
		getrt(v,u),siz[u]+=siz[v];
		ckmax(mx[u],siz[v]);
	}
	ckmax(mx[u],tsiz-siz[u]);
	if(mx[u]<mx[rt])rt=u;
}
bool qwq[N];
void solve(int x){
	used[x]=1;
	for(int i=x;i;i=vt[i]){
		R1[i]+=a[x]*dis(i,x),R3[i]+=a[x];
		if(vt[i])R2[i]+=a[x]*dis(vt[i],x);
	}
	for(int i=hed[x];i;i=e[i].nx){
		int y=e[i].to;if(used[y])continue;
		tsiz=siz[y],rt=0,getrt(y,x),vt[rt]=x,solve(rt);
	}
}
LL calc(int x){
	LL res=R1[x];
	for(int i=x;vt[i];i=vt[i])
		res+=R1[vt[i]]-R2[i]+(R3[vt[i]]-R3[i])*dis(vt[i],x);
	return res;
}
void upd(int x,int y){
	for(int i=x;i;i=vt[i]){
		R1[i]+=y*dis(i,x),R3[i]+=y;
		if(vt[i])R2[i]+=y*dis(vt[i],x);
	}
}

void change(int x,int y){
	D+=calc(x)*(y-a[x]),S+=y-a[x],upd(x,y-a[x]),a[x]=y;
}
LL query(int x){return S*(calc(x)+S)-D;}
void build(){mx[rt=0]=tsiz=n,getrt(1,0),solve(rt);}
}
signed main(){
	n=read(),q=read();
	rep(i,2,n){
		int x=read(),y=read();
		adde(x,y),adde(y,x);
	}
	rep(i,1,n)a[i]=read(),S+=a[i];
	Tree::dfs1(1,0),Tree::dfs2(1,1);
	DFZ::build();
	while(q--){
		int op=read(),x=read();
		if(op==1)DFZ::change(x,read());
		else printf("%lld\n",DFZ::query(x));
	}
	return 0;
}