三维凸包 学习笔记

三维凸包 学习笔记

P4724 【模板】三维凸包

一些计算几何基础

三维空间内给一堆点，求其三维凸包的表面积。

其实体积也能求，最后会写。

首先要一个三维向量来表示点，方便计算。

const double eps=1e-9;
double randeps() {return (rand()/(double)RAND_MAX-0.5)*eps;}
struct vec {
	double x,y,z;
	vec(){x=y=z=0;}
	vec(double x_,double y_,double z_){x=x_,y=y_,z=z_;}
	void shake() {x+=randeps(),y+=randeps(),z+=randeps();}
	double len() {return sqrt(x*x+y*y+z*z);}
	vec operator + (const vec &t) {return vec(x+t.x,y+t.y,z+t.z);}
	vec operator - (const vec &t) {return vec(x-t.x,y-t.y,z-t.z);}
}p[N];
double dot(const vec &a,const vec &b) {return a.x*b.x+a.y*b.y+a.z*b.z;}
vec crs(const vec &a,const vec &b) {return vec(a.y*b.z-a.z*b.y,a.z*b.x-a.x*b.z,a.x*b.y-a.y*b.x);}

几个注意事项：

• 三维向量的叉积不是数，还是向量，方向垂直于叉积的两个向量所在的平面，模长就是有向面积。
• 大家会发现有个shake函数。那个是为了防止四点共面，否则在后面求凸包的过程会出错。

关于如何记录凸包：考虑到凸包是由一堆平面，直接按照逆时针方向记录每个面的三个点（之前防止四点共面的原因）

struct face {
	int v[3];
	face(){v[0]=v[1]=v[2]=0;}
	face(int a,int b,int c) {v[0]=a,v[1]=b,v[2]=c;}
	vec normal() {return crs(p[v[1]]-p[v[0]],p[v[2]]-p[v[0]]);}//叉积，模长是面积的2倍
	double area() {return normal().len()/2.0;}//面积
}cv[N],h[N];

构造凸包

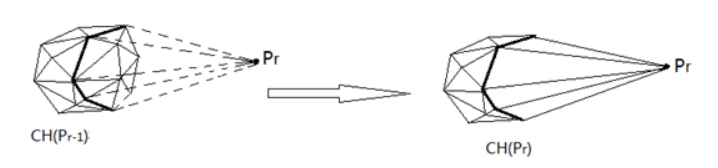
(引自博客https://www.cnblogs.com/-sunshine/archive/2012/08/25/2656794.html)

大概就是这么张图。

增量法构造，每次加入一个点，把它看不见的点保留在凸包内，然后把上图加粗的棱与新增的点组成一个面，加入凸包。

• 判定能否看到：把那个face的normal（法向量）与新增的点点乘，看正负。看得到则为正。（其实就是看与法向量的夹角，判断点是否在平面上方）
• 判断粗边。代码中体现为 \(vis[x][y]\&\&!vis[y][x]\) 。那么xy就是分割线。

模拟上述过程即可，复杂度 \(O(n^2)\)：

int cansee(face A,vec b) {return dot(b-p[A.v[0]],A.normal())>0;}
int n,th,cnt,vis[N][N];
double ans;
void convex() {
	cnt=th=0;
	cv[++cnt]=face(1,2,3);
	cv[++cnt]=face(3,2,1);
	for(rint i=4;i<=n;++i) {
		for(rint j=1,v;j<=cnt;++j) {
			if(!(v=cansee(cv[j],p[i])))h[++th]=cv[j];
			for(rint k=0;k<3;++k) 
				vis[cv[j].v[k]][cv[j].v[k>1?0:k+1]]=v;
		}
		for(rint j=1;j<=cnt;++j)
			for(rint k=0;k<3;++k) {
				int x=cv[j].v[k],y=cv[j].v[k>1?0:k+1];
				if(vis[x][y]&&!vis[y][x])h[++th]=face(x,y,i);
			}
		for(rint j=1;j<=th;++j)cv[j]=h[j];
		cnt=th,th=0;
	}
}

凸包构造完毕！

计算表面积的话，把每个面的normal的模长加起来除以2.

模板题代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned int uint;
#define rint register int
#define pb push_back
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2) EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
inline int rd() {
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+(ch^48),ch=getchar();
    return x*f;
}
const int N=2010;
const double eps=1e-9;
double randeps() {return (rand()/(double)RAND_MAX-0.5)*eps;}
struct vec {
	double x,y,z;
	vec(){x=y=z=0;}
	vec(double x_,double y_,double z_){x=x_,y=y_,z=z_;}
	void shake() {x+=randeps(),y+=randeps(),z+=randeps();}
	double len() {return sqrt(x*x+y*y+z*z);}
	vec operator + (const vec &t) {return vec(x+t.x,y+t.y,z+t.z);}
	vec operator - (const vec &t) {return vec(x-t.x,y-t.y,z-t.z);}
}p[N];
double dot(const vec &a,const vec &b) {return a.x*b.x+a.y*b.y+a.z*b.z;}
vec crs(const vec &a,const vec &b) {return vec(a.y*b.z-a.z*b.y,a.z*b.x-a.x*b.z,a.x*b.y-a.y*b.x);}
struct face {
	int v[3];
	face(){v[0]=v[1]=v[2]=0;}
	face(int a,int b,int c) {v[0]=a,v[1]=b,v[2]=c;}
	vec normal() {return crs(p[v[1]]-p[v[0]],p[v[2]]-p[v[0]]);}
	double area() {return normal().len()/2.0;}
}cv[N],h[N];
int cansee(face A,vec b) {return dot(b-p[A.v[0]],A.normal())>0;}
int n,th,cnt,vis[N][N];
double ans;
void convex() {
	cnt=th=0;
	cv[++cnt]=face(1,2,3);
	cv[++cnt]=face(3,2,1);
	for(rint i=4;i<=n;++i) {
		for(rint j=1,v;j<=cnt;++j) {
			if(!(v=cansee(cv[j],p[i])))h[++th]=cv[j];
			for(rint k=0;k<3;++k) 
				vis[cv[j].v[k]][cv[j].v[k>1?0:k+1]]=v;
		}
		for(rint j=1;j<=cnt;++j)
			for(rint k=0;k<3;++k) {
				int x=cv[j].v[k],y=cv[j].v[k>1?0:k+1];
				if(vis[x][y]&&!vis[y][x])h[++th]=face(x,y,i);
			}
		for(rint j=1;j<=th;++j)cv[j]=h[j];
		cnt=th,th=0;
	}
}
void calc() {for(rint i=1;i<=cnt;++i)ans+=cv[i].area();}
signed main() {
	srand(time(0));
	n=rd();
	for(rint i=1;i<=n;++i)
		scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z),p[i].shake();
	convex();calc();
	printf("%.3lf\n",ans);
	return 0;
}

计算体积：darkbzoj #1964. hull 三维凸包

只需要在构造出凸包后更改calc函数，每次计算 p[1] 与每个面组成三棱锥的体积，相加即可。

这个用向量很方便：

double vol6(vec a,vec b,vec c,vec d) {
	return dot(crs(b-a,c-a),d-a);
} //计算体积的6倍。理解：先算出底的有向面积的2倍，向量的方向变为高，然后点乘就是另一条边在高方向的投影，由体积公式(V=1/3*Sh)，这个值就是体积的6倍
void calc() {
	for(rint i=1;i<=cnt;++i)
		ans+=fabs(vol6(p[1],p[cv[i].v[0]],p[cv[i].v[1]],p[cv[i].v[2]]));
	ans/=6;
}