题解 P4288 【[SHOI2014]信号增幅仪】

题意

在一个二维平面上给定 \(n\) 个点，求最小的椭圆短轴长包含所有点，给定常数 \(p\) ，表示长轴是短轴的 \(p\) 倍，给定常数 \(a\) ，为长轴与 \(x\) 轴的夹角

思路

斜着的椭圆不是很好算，考虑把所有点顺时针转 \(a\) 度。

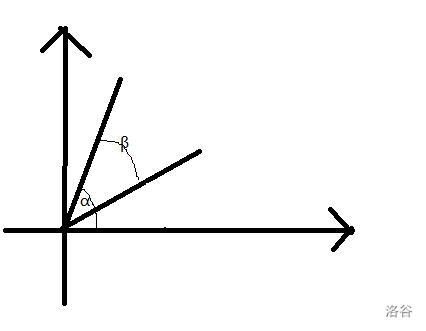
设任意一点 \(A(x,y)\) ，它到原点的距离是 \(r\) 那么 \(A(r\cos(\alpha),r\sin(\alpha))\)

顺时针转动 \(\beta\) 后 \(A'(r\cos(\alpha-\beta),r\sin(\alpha-\beta))\)

用差角公式展开得 \(A'(r(cos\alpha\cos\beta+sin\alpha\sin\beta),r(sin\alpha\cos\beta-sin\beta\cos\alpha))\)

而 \(r\cos\alpha=x,r\sin\alpha=y\)

按照乘法分配律提出得 \(A'(x\cos\beta+y\sin\beta,y\cos\beta-x\sin\beta)\)

\(\beta\) 的角度已知，那么 \(\dfrac{\beta\cdot\pi}{180}\) 即为弧度，带入上式即可求出旋转后每个点的坐标

椭圆也不是很方便，发现如果把每个点的横坐标除以 \(p\) 即可把椭圆换成圆。

通过上述变换，现在的问题变成了“给定 \(n\) 个点，求出最小的圆心和半径覆盖所有点”

先提一下某同学的思路：爬山或者模拟退火找圆心。没了。

但是每个人都应该知道 OI 赛制退火的后果（

事实上有一种线性求最小圆覆盖的方法：https://www.luogu.com.cn/blog/boshi/solution-p1742（也可以上百度搜qwq）

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned int uint;
#define rint register int
#define pb push_back
//#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2) EOF:*p1++)
//char buf[1<<21],*p1=buf,*p2=buf;
inline int rd() {
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch))x=x*10+(ch^48),ch=getchar();
	return x*f;
}
const int N=1e5+10;
const double pi=acos(-1.0);
struct vec {
	double x,y;
	vec(){x=y=0;}
	vec(double _x,double _y){x=_x,y=_y;}
	vec operator + (const vec &t)const{return vec(x+t.x,y+t.y);}
	vec operator - (const vec &t)const{return vec(x-t.x,y-t.y);}
	vec operator * (const double &t)const{return vec(x*t,y*t);}
	vec operator / (const double &t)const{return vec(x/t,y/t);}
	vec rot_90() {return vec(y,-x);}
	double len2() {return x*x+y*y;}
}p[N],O;
double R;
int n;
double cross(const vec &a,const vec &b) {
	return a.x*b.y-a.y*b.x;
}
vec inter(const vec &p1,const vec &v1,const vec &p2,const vec &v2) {
	double t=cross(p2-p1,v2)/cross(v1,v2);
	return p1+v1*t;
}
vec circle(const vec &a,const vec &b,const vec &c) {
	return inter((a+b)/2,(b-a).rot_90(),(b+c)/2,(c-b).rot_90());
}
void min_circle() {
	random_shuffle(p+1,p+n+1);
	R=0;
	for(rint i=1;i<=n;++i) {
		if((p[i]-O).len2()>R) {
			O=p[i],R=0;
			for(rint j=1;j<i;++j) {
				if((p[j]-O).len2()>R) {
					O=(p[i]+p[j])/2,R=(p[i]-O).len2();
					for(rint k=1;k<j;++k) {
						if((p[k]-O).len2()>R) {
							O=circle(p[i],p[j],p[k]),R=(p[i]-O).len2();
						}
					}
				}
			}
		}
	}
	R=sqrt(R);
}
double A,P;
signed main() {
	srand(time(0));
	n=rd();
	for(rint i=1;i<=n;++i) scanf("%lf%lf",&p[i].x,&p[i].y);
	A=1.0*rd()*pi/180,P=rd();
	for(rint i=1;i<=n;++i) {
		double X=p[i].x,Y=p[i].y;
		p[i].x=X*cos(A)+Y*sin(A);
		p[i].y=Y*cos(A)-X*sin(A);
		p[i].x/=P;
	}
	min_circle();
	printf("%.3lf\n",R);
	return 0;
}