基于梯度下降法进行参数优化学习
感知器的训练
首先将权重w和 偏置b随机初始化为一个很小的数,然后在训练中不断更新w和b的值,使得损失函数更小。
1.将权重初始化为 0 或一个很小的随机数
2.对于每个训练样本 x(i) 执行下列步骤:
计算输出值 y^.
更新权重
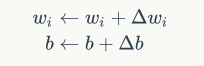
其中
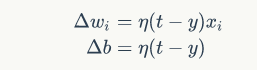
下面用感知器实现and操作,具体代码如下:
# -*- coding: utf-8 -*-
import numpy as np
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Perceptron
from sklearn.model_selection import train_test_split
def load_data():
input_data = np.array([[1, 1], [0, 0], [1, 0], [0, 1]])
labels = np.array([1, 0, 0, 0])
return input_data, labels
def train_pre(input_data, y, iteration, rate):
clf = Perceptron(random_state=0, eta0=rate, max_iter=iteration)
clf.fit(input_data, y)
w, bias = clf.coef_[0], clf.intercept_[0]
return w, bias
def predict(input_i, w, b):
result = np.dot(input_i, w) + b
y_pred = int(result > 0)
print(y_pred)
if __name__ == '__main__':
input_data, y = load_data()
w, b = train_pre(input_data, y, 20, 0.1)
predict([0, 0], w, b)
- 感知机的函数表示,对任意函数g(t),对它数值采样,然后用感知机去表示出来。
例如 g(t)=sin(t),t∈[0,1],采样ti=(i)/n,xi=g(ti),i=0,2,...,n;选激活函数f(x,y),其定义如下:
设采样点为Pi=(ti,g(ti)),感知机模型如下
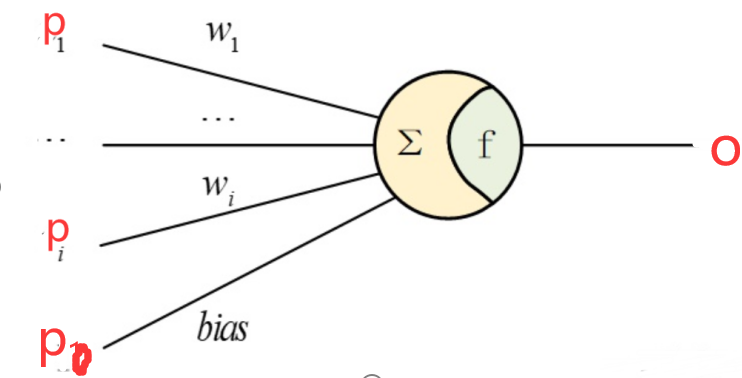
则上述感知机的输出是:
,
直接选模型参数如下:
编程实现,并画出实验结果图形。
import numpy as np
import matplotlib.pyplot as plt
# 定义激活函数 f(x,y)
def f(x,y):
if x >= 0 and x <= 1:
return (x, y)
else:
return (0, 0)
# 定义函数 g(t)
def g(t):
return np.sin(t)
# 采样数据
n = 50
t = np.linspace(0, 1, n)
p = [(t[i], g(t[i])) for i in range(n)]
# 计算感知机参数
w = np.zeros(n)
for i in range(n):
w[i] = np.math.comb(n, i) * (i/n)**i * ((n-i)/n)**(n-i)
# 计算感知机输出
x = np.linspace(0, 1, 100)
y = np.zeros(100)
for j in range(100):
o = np.dot(w, np.array([f(p[i][0] - x[j], p[i][1]) for i in range(n)]))
y[j] = o[0]
# 绘制图像
plt.plot(x, g(x), label='g(t)')
plt.plot(x, y, label='Perceptron')
plt.legend()
plt.show()
实验结果:
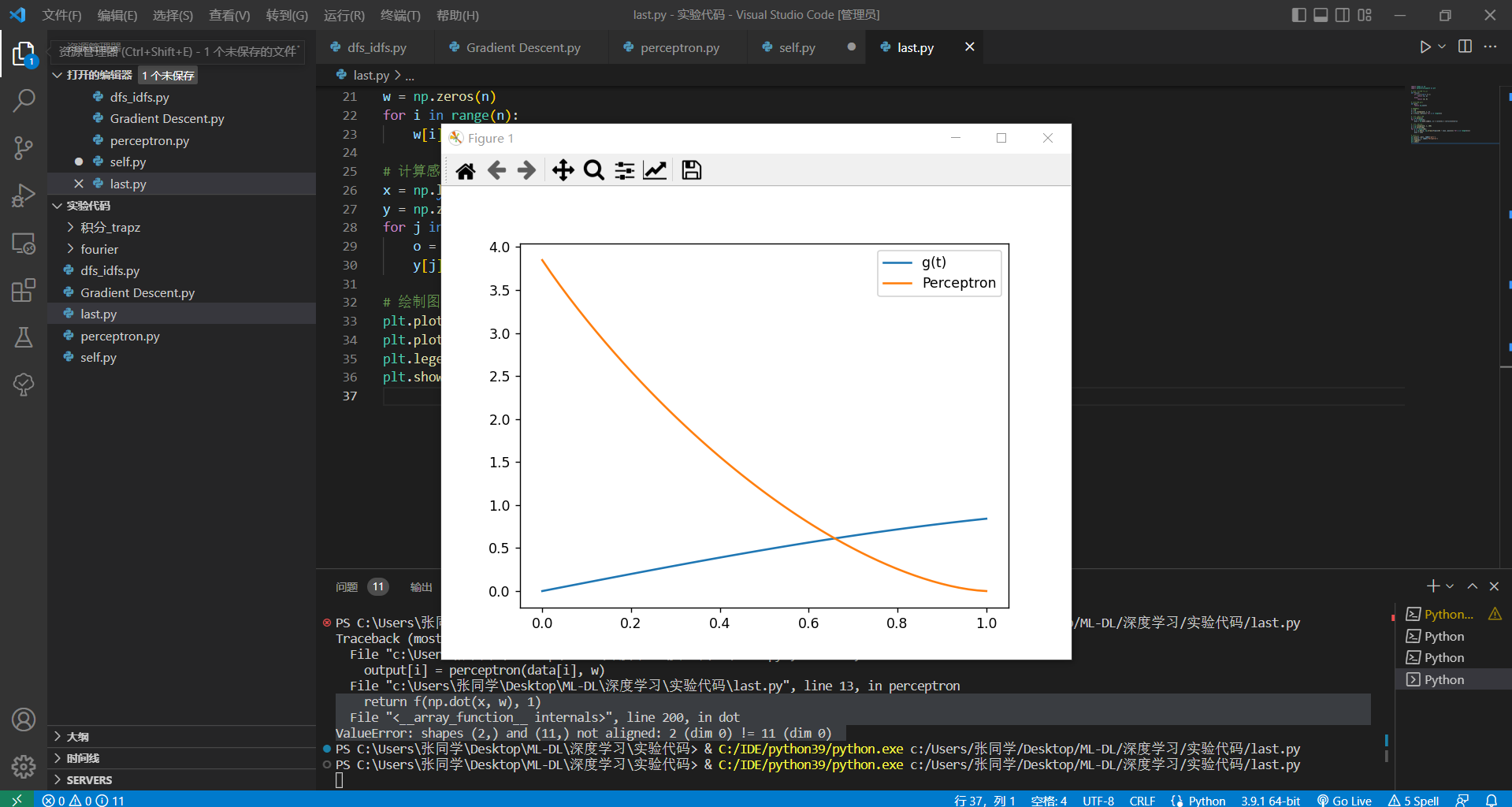



 浙公网安备 33010602011771号
浙公网安备 33010602011771号