DFS（一）：砌墙问题

问题描述

使用两种砖头砌墙，砖头A宽为2，高为1，砖头B宽为3，高为1，用这两种砖头砌一面宽为W，高为H的墙。

为了使墙牢固性高，要求每种砖只能横向摆放，不能竖起来，且除了两侧以外，不能出现上下对齐的砖缝，请参考下图： 

     

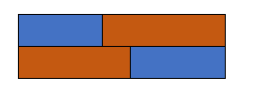
上图允许

 

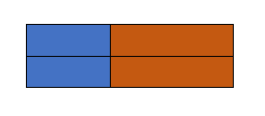
上图不允许

下图展示了宽为13，高为5的墙的一种砌法

 

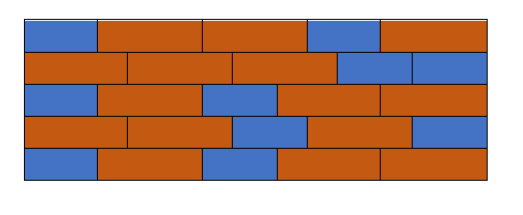
对于给定的宽度W，高度H，请问有多少种砌法？

解决方案

该问题可以转化为搜索问题，使用深度优先搜索即可解决。

具体思路是：将墙转化为2维平面坐标系，使用二维字符数组记录砖缝的位置，放置砖块时，判断是否可行，不行则回溯。

从源点出发，向右上方进行递归搜索，直到搜索到对角顶点处，便得到了一种砌法，程序结束时，所有的砌法都已经被搜索到。

代码实现（c++)

#include<iostream>
#include<string>
#define yes 1
#define no 0
using namespace std;
static int kind = 0;//可行的方案数 
static int H,W;
//判断是否可以在该位置放置砖块 
int IsOk(string abv, int w){
    if(w>W)
        return no;
    else if (w==W)
        return yes;
    return (abv[w]-'0')?no:yes;
}
//深搜 
void dfs(int h, int w, string above[]){
    if(h == (H+1)){   //搜索的出口，输出合适的方案 
        kind ++;
        for(int i=1;i<=H;i++)
            cout<<above[i]<<endl;
        cout<<"---------------"<<endl;
        return;
    }
    for(int i = 2; i <=3; i++){
        if(IsOk(above[h-1], w+i)){
            above[h][w+i] = '1';   //放置砖块，标记砖缝位置。 
            if((w+i)==W)
                dfs(h+1, 0, above);
            else 
                dfs(h, w+i, above);
            above[h][w+i] = '0';  //回溯，搜索另一条路径。 
        }
    }
    return;
}

int main(){
    cin>>W;
    cin>>H;
    string above[H+1];
    for(int i = 0; i <= H; i++){   //初始化字符串数组，用来记录砖缝位置。 
        above[i] = '1';
        for(int j = 1; j <= W; j++)
            above[i] += '0';
        }
    dfs(1, 0, above);
    cout<<kind<<endl;
}

运行结果

输入：宽度9，高度5。

输出：14