机器学习问题之屌丝的女神专属
转载请注明出处[zz_boy]:http://www.cnblogs.com/zz-boy/p/3648434.html
欢迎大家访问我的其它博客,我的博客园主页:http://www.cnblogs.com/zz-boy/
每个屌丝都有自己的女神专属
屌丝的通病便是眼神不老实。走在街上,看到漂亮妹子情不自禁要多瞟几眼,如果是两三屌丝在一起,时不时还要品评一番,如果一群屌丝只有你觉得这个妹子漂亮,一般情况下是要恭喜你的,因为你总不免要被嘲笑一番,然后大家一致得出结论你审美能力低下;当然这种极端的情况很少出现,对一个妹子,总有些屌丝觉得漂亮,有些屌丝不置可否。万千屌丝在极端无聊的情况下,发明了一种惨无人道,侵犯人权的对漂亮的量化方法,打分!看到一个妹子,1到10的区间,每个屌丝给出一个分数,这种例子在我身边发生了无数次,听多了,某一天,愚钝的我好像被树上掉下来的苹果砸了一下。我发现对同一个妹子,不同的屌丝给出来的分数差别很大,经过一番思考,我捡起掉在地上的苹果,咬了一口,自言自语道:“每个屌丝的审美观是不同的”。
在我咬下一口之前,我决定想一想为什么屌丝们的审美观会不同,当然了,我不想将问题扩大化,免得被不怀好意的人利用,就好像当年润芝兄搞什么整风,革命之类的一样,我还是将问题局限在女人。首先我想到的是屌丝们的妈长得不一样,忘记在哪里看到的,说屌丝们总觉得像他妈的女人更漂亮一点,我狠狠的咬了一口苹果。其次我想到的是,屌丝们长得不一样,这个结论是我用肉眼观察了大量的高富帅和他身边像鸟一样的女人之后得出来的结论,嗯,他们长得很像,冥冥之中,屌丝也在寻找和他长得很像的女神。再次,屌丝们的教育背景不一样,有些屌丝身上有书卷气,他们往往喜欢沉静,温婉一点的女孩,有些屌丝,身上有流氓气,《野蛮女友》是他们的最爱,当然除此以外,还有屌丝的年龄,父母有没有离过婚,有没有看过断背山等等因素,这些共同决定了屌丝的审美。
这里忍不住要吐槽一下妹子,初次见面,或者就是擦肩而过,屌丝对女神他粑粑的长相,女神有没有看过美丽在唱歌,女神爸妈有没有离婚这些都不了解,映入屌丝眼帘的是妹子飘逸的秀发,优雅的脚步,活泼的眼神,整齐的衣着;屌丝的世界屌丝自己都不懂,屌丝觉得自己和女神根本不在一个次元,屌丝糊涂了,特征空间都不相同,都没法用余弦相似度,“我是怎么判断我喜不喜欢那个妹子的?”屌丝自言自语。
看着手中不剩几口的苹果,忽然领悟到刚才被砸中却不怎么疼的原因,我想牛顿当年被苹果砸了,那该是几吨重的苹果;牛顿没被砸死,抓住上帝的失误不放,勒索到了经典力学的秘密,当然牛顿付出的代价是惨重的,他二十几岁之后的人生都做了上帝的奴仆。还好砸我的苹果很小,苹果的秘密已经被牛顿公诸于世了,斯人已往矣,上帝总不至于抓我去做他的奴仆,瞬间,我坚定了继续扒的勇气。
膜在哪里
屌丝很悲哀,屌丝的世界没有初次见面,只有擦肩而过,屌丝的回眸不能倾国倾城,只能得出一个猥琐的分数。
“你打多少分?”
“7.2”
“次奥,是不是你妈长得太丑了,无语。我给9.0分。”
正如上面说的,屌丝和妹子处在不同的特征空间,屌丝到底是怎么判断喜不喜欢那个妹子的?
屌丝仔细回想妈咪的长相,妈咪长头发,着装整齐干净,步态优雅,屌丝忽然又想到他的女神,飘逸的秀发,优雅的脚步,活泼的眼神,整齐的衣着。屌丝若有所悟,瞬间来了精神,屌丝斗转思绪,想到自己身上的书卷气,自言自语道:“书卷气和飘逸的秀发较之书卷气和圆寸头联系更紧密一点,书卷气和优雅的脚步较之书卷气和快速沉重的步伐联系紧密一点,啊,原来如此”。屌丝像窥探到上帝的秘密一样开心,原来自己特征空间中的每一维和女神特征空间中的每一维都有关系,这样的关系或紧或松。
你们都是第一次
为了量化这个问题,我想先做一些定义:
屌丝的特征向量X: (x1,…,xm)T
妹子的特征向量Z: (z1,…,zn)T
屌丝i对妹子的j的评分:rij
我们用Wm*n矩阵来量化屌丝特征空间的每一维与女神特征空间的每一维之间关联的紧密程度。wa,b表示屌丝特征空间第a维和女神特征空间第b维联系的紧密程度,越大越紧密。
当屌丝又一次和妹子擦肩而过的时候,屌丝瞬间获取到妹子的特征向量zj,我们猜测屌丝i可能给出的评分sij。
矩阵W是未知数,我们要做的事情就是求出W从而建立屌丝对女神评分的模型,建立这个模型还需要大量的屌丝评分样本,我们假设已经有这样的样本O。
我们定义误差函数如下:
扒到这里膜便找到了,这是一个优化问题,我们要做的就是最小化error(w),可以用梯度下降的方法很容易求解出W。
轻车熟路的老鸟
老鸟们觉得任何一个未知参数,都是一个随机变量,应该使用一个概率分布去描述变量的未知情况,这个分布是对抽样之前就有的变量的先验信息的概率陈述。老鸟驾驭参数估计也是那么的斗志高昂,“冲刺!冲刺!!”,老鸟高喊党的口号。
老鸟轻而易举的就写下了下面的公式:
一看就是贝爷的子子孙孙,真相越发明了,司马昭之心路人皆知,现在缺的就是先验分布以及似然函数了。
高斯先验分布:
似然函数:
根据元误差学说,误差是由大量的、由种种原因产生的元误差叠加而成,因此可以使用高斯分布作为误差的分布:
使用最大后验估计(MAP),这个优化问题等同于最小化下面的负对数联合概率:
仍然可以使用梯度下降的方法处理:
云上的日子
事情总有个了断。清晨,苏菲睁开眼睛,一夜的云雨,让苏菲感觉很是疲乏,习惯性的看向枕边,却发现除了枕头上的凹痕,身边空空如也,苏菲瞬间清醒了好多,一股习惯性的厌恶感涌上心头,情不自禁骂道,“屌丝!”,是的,苏菲已经习惯了。
屌丝披着黎明前的夜色走了,屌丝走的很悲怆,他还是眷恋这里的,他甚至半夜里,趁着苏菲睡着,偷偷地钻到床底,在床板上刻下了“zz到此一游”的悲壮语句,但屌丝不得不走,因为他必须在路上,只有这样他才能用下面的公式验证预测模型的正确性:
屌丝今夜重又走入风雨,为了生命的远行,为了不安分的心。
欢迎大家访问我的其它博客,我的博客园主页:http://www.cnblogs.com/zz-boy/

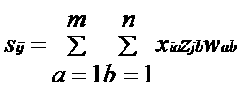
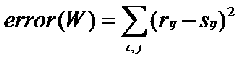
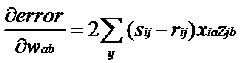
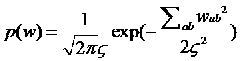
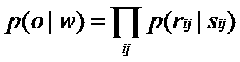
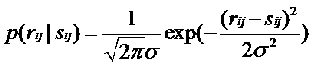
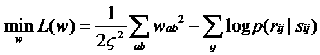
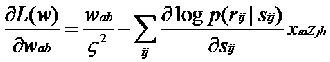
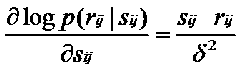
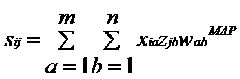


 浙公网安备 33010602011771号
浙公网安备 33010602011771号