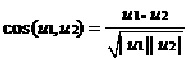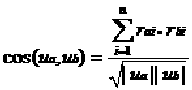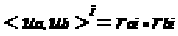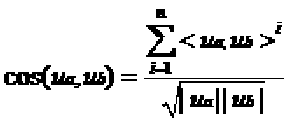大规模稀疏向量余弦相似度计算方法（续）

大规模稀疏向量余弦相似度计算方法（续）

转载请注明出处(zz_boy):http://www.cnblogs.com/zz-boy/archive/2012/12/15/2819401.html

向量u₁和u₂的余弦相似度计算公式如下

我们将向量表示成矩阵R_m*n，如下所示

	d­1	d2	d3	d4	…	dn
u1	r11	r12	r13	r14	…	r1n
u2	r21	r22	r23	r24	…	r2n
u3	r31	r32	r33	r34	…	r3n
…	…	…	…	…	…	…
um	rm1	rm2	rm3	rm4	…	rmn

r_ij表示向量u_i的第j维（d_j）的值。

那么u_a和u_b的余弦相似度可以表示成如下的公式

我们假设

那么上面的公式可以改写成

因此u_a和u_b的余弦相似度计算可以抽象成n+1部计算。

前n部是对求和，最后一步是除以分母。

基于上面的理论，我们提出一种使用外排序的方法计算相似度的方法，该方法在应对大规模数据时可以有效地控制内存使用，并且计算效率很高。

算法：

建立d-><u,r>的倒排索引(r!=0)；

对向量空间的每一维度d_i

根据上面建立的倒排索引获取关联的{<u,r>};假设为{<u_a,r_ai>,<u_b,r_bi>,<u_c,r_ci>}，其中u_a< u_b< u_c;

穷尽{<u,r>}中所有的两两组合，生成待排序项追加到外存文件中。比如上面的{<u_a,r_ai>,<u_b,r_bi>,<u_c,r_ci>}，我们将生成以下排序项：

< u_a , u_b , r_ai * r_bi >,< u_a , u_c , r_ai * r_ci >,< u_b , u_c , r_bi * r_ci >

使用外存归并排序方法对文件排序，上述三元组的第一维是主排序项，第二维度是次排序项，归并过程中，如果发现buffer中最近的三元组主排序项、次排序项和当前要添加到buffer中的三元组都相同，则立即合并他们，合并的方法是将两个三元组的第三维相加，前两维不变生成新的三元组，并替换被合并的两个记录。

比如buffer中最近的是< u_a , u_b , r₁>，外存归并排序败者树得出的记录是< u_a , u_b , r₂>，则用

< u_a , u_b , r₁+r₂>替换buffer中的< u_a , u_b , r₁>。

入库时每取出一个三元组，则将此三元组的第三维除以已经计算好的分母（余弦相似度计算公式）。

算法优点分析：

1. 算法只会访问r!=0的位置，这对于大规模稀疏向量而言无疑大大加快了速度。

2. 外存归并排序可以定制归并路数K，对每一路可以限制buffer的大小，因此无论数据量有多大，排序所需的内存都是可以控制的。

3. 使用败者树的外存归并排序方法，排序效率很高，因此其处理速度很快，实验中我使用了6000*6000的矩阵，矩阵中不为0的位置有一千万个，机器配置如图所示

外排用时75s.

4. 使用上述方法计算相似度是便于动态更新的。这是因为我们可以轻松的以在外排序文件末尾追加记录（三元组）的方式实现相似度的更新，追加的三元组第三维为负值表示要减少原始的计算结果，正值表示增加原始的计算结果。