30 (OC)* 数据结构和算法
在描述算法时通常用o(1), o(n), o(logn), o(nlogn) 来说明时间复杂度
o(1):是最低的时空复杂度,也就是耗时/耗空间与输入数据大小无关,无论输入数据增大多少倍,耗时/耗空间都不变。 哈希算法就是典型的O(1)时间复杂度,无论数据规模多大,都可以在一次计算后找到目标(不考虑冲突的话)
哈希算法。
O(n):代表数据量增大几倍,耗时也增大几倍。(n)代表输入的数据量,比如常见的遍历算法
O(n^2):代表数据量增大n倍,时间复杂度就是n的平方倍,比如冒泡排序,就是典型的O(n^2)的算法,对n个数排序,需要扫描n×n次。
O(logn):当数据增大n倍时,耗时增大logn倍(这里的log是以2为底的,比如,当数据增大256倍时,耗时只增大8倍,是比线性还要低的时间复杂度)。二分查找就是O(logn)的算法,每找一次排除一半的可能,256个数据中查找只要找8次就可以找到目标
O(nlogn):同理,就是n乘以logn,当数据增大256倍时,耗时增大256*8=2048倍。这个复杂度高于线性低于平方。归并排序就是O(nlogn)的时间复杂度。
一、排序
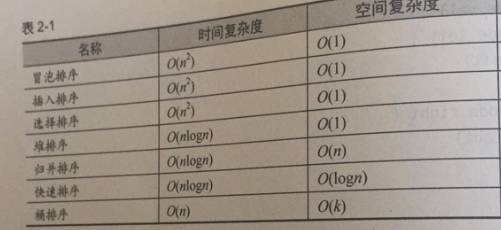
排序法 平均时间 最差情形 稳定度 额外空间 备注
冒泡 O(n2) O(n2) 稳定 O(1) n小时较好
交换 O(n2) O(n2) 不稳定 O(1) n小时较好
选择 O(n2) O(n2) 不稳定 O(1) n小时较好
插入 O(n2) O(n2) 稳定 O(1) 大部分已排序时较好
Shell O(nlogn) O(ns) 1<s<2 不稳定 O(1) s是所选分组
快速 O(nlogn) O(n2) 不稳定 O(nlogn) n大时较好
归并 O(nlogn) O(nlogn) 稳定 O(1) n大时较好
堆 O(nlogn) O(nlogn) 不稳定 O(1) n大时较好
基数 O(logRB) O(logRB) 稳定 O(n) B是真数(0-9),R是基数(个十百)
数据结构通常分为四类:
1.集合结构 线性结构 树形结构 图形结构
1.1、集合结构:就是一个集合,就是一个圆圈中有很多个元素,元素与元素之间没有任何关系 。
1.2、线性结构 :就是一个条线上站着很多个人。 这条线不一定是直的。也可以是弯的。也可以是值的 相当于一条线被分成了好几段的样子。 线性结构是一对一的关系。
1.3、树形结构 :做开发的肯定或多或少的知道xml 解析 树形结构跟他非常类似。也可以想象成一个金字塔。树形结构是一对多的关系
1.4、图形结构:这个就比较复杂了。 无穷、无边、 无向(没有方向)图形机构 你可以理解为多对多 类似于我们人的交集关系。
2. 数据结构的存储
数据结构的存储一般常用的有两种 顺序存储结构 和 链式存储结构。
2.1 顺序存储结构
举个列子。数组。1-2-3-4-5-6-7-8-9-10。这个就是一个顺序存储结构 ,存储是按顺序的 栈。做开发的都熟悉。栈是先进后出 ,后进先出的形式。hello world 在栈里面从栈底到栈顶的逻辑依次为 h-e-l-l-o-w-o-r-l-d 这就是顺序存储 再比如 队列 ,队列是先进先出的对吧,从头到尾 h-e-l-l-o-w-o-r-l-d 就是这样排对的。
2.2 链式存储结构
1-2-3-4-5-6-7-8-9-10 链式存储就不一样了 1(地址)-2(地址)-7(地址)-4(地址)-5(地址)-9(地址)-8(地址)-3(地址)-6(地址)-10(地址)。每个数字后面跟着一个地址 而且存储形式不再是顺序 ,也就说顺序乱了,1(地址) 1后面跟着的这个地址指向的是2,2后面的地址指向的是3,3后面的地址指向是谁你应该清楚了吧。他执行的时候是 1(地址)-2(地址)-3(地址)-4(地址)-5(地址)-6(地址)-7(地址)-8(地址)-9(地址)-10(地址),但是存储的时候就是完全随机的。
3. 单向链表\双向链表\循环链表
3.1 单向链表
A->B->C->D->E->F->G->H. 这就是单向链表 H 是头 A 是尾 像一个只有一个头的火车一样 只能一个头拉着跑
3.2 双向链表
H<- A->B->C->D->E->F->G->H. 这就是双向链表。有头没尾。两边都可以跑 跟地铁一样 到头了 可以倒着开回来
3.3 循环链表
A->B->C->D->E->F->G->H. 绕成一个圈。就像蛇吃自己的这就是循环。
4.二叉树/平衡二叉树
4.1 什么是二叉树
树形结构下,两个节点以内 都称之为二叉树 不存在大于2 的节点 分为左子树 右子树 有顺序 不能颠倒。
二叉树有五种表现形式
1. 空的树(没有节点)可以理解为什么都没 像空气一样
2. 只有根节点。 (理解一个人只有一个头 其他的什么都没,说的有点恐怖)
3. 只有左子树 (一个头 一个左手 感觉越来越写不下去了)
4. 只有右子树
5 、左右子树都有
二叉树可以转换成森林 树也可以转换成二叉树。
5.算法,冒泡排序、选择排序、插入排序、快速排序、二分法查找、希尔排序、戴克斯特拉算法,快捷算法,动态规划,堆排序,归并排序。
5.1 冒泡排序
1. 首先将所有待排序的数字放入工作列表中。
2. 从列表的第一个数字到倒数第二个数字,逐个检查:若某一位上的数字大于他的下一位,则将它与它的下一位交换。
3. 重复2号步骤(倒数的数字加1。例如:第一次到倒数第二个数字,第二次到倒数第三个数字,依此类推...),直至再也不能交换。
平均时间复杂度:O(n^2)
平均空间复杂度:O(1)
-(void)maoPao{//冒泡排序
NSMutableArray *arr=[NSMutableArray arrayWithArray:@[@"17",@"28",@"36",@"15",@"29",@"39"]];
for (int i=0;i<arr.count;i++) {
for (int j=0; j<arr.count-1-i; j++) {
if ([arr[j] intValue]>[arr[j+1] intValue]) {
int temp=[arr[j] intValue];
arr[j]=arr[j+1];
arr[j+1]=[NSString stringWithFormat:@"%d",temp];
}
}
}
NSLog(@"%@",arr);
}
5.2 选择排序
1. 设数组内存放了n个待排数字,数组下标从1开始,到n结束。
2. i=1
3. 从数组的第i个元素开始到第n个元素,寻找最小的元素。(具体过程为:先设arr[i]为最小,逐一比较,若遇到比之小的则交换)
4. 将上一步找到的最小元素和第i位元素交换。
5. 如果i=n-1算法结束,否则回到第3步
平均时间复杂度:O(n^2)
平均空间复杂度:O(1)
-(void)xuanZe{//选择排序
NSMutableArray *arr=[NSMutableArray arrayWithArray:@[@"17",@"28",@"36",@"15",@"29",@"39"]];
for (int i=0;i<arr.count-1;i++) {
for (int j=i+1; j<arr.count; j++) {
if ([arr[i] intValue]>[arr[j] intValue]) {
int temp=[arr[i] intValue];
arr[i]=arr[j];
arr[j]=[NSString stringWithFormat:@"%d",temp];
}
}
}
NSLog(@"%@",arr);
}
5.3 插入排序
1. 从第一个元素开始,认为该元素已经是排好序的。
2. 取下一个元素,在已经排好序的元素序列中从后向前扫描。
3. 如果已经排好序的序列中元素大于新元素,则将该元素往右移动一个位置。
4. 重复步骤3,直到已排好序的元素小于或等于新元素。
5. 在当前位置插入新元素。
6. 重复步骤2。
平均时间复杂度:O(n^2)
平均空间复杂度:O(1)
-(void)chaRu{//插入排序
NSMutableArray *arr=[NSMutableArray arrayWithArray:@[@"17",@"28",@"36",@"15",@"29",@"39"]];
for (int i=1;i<arr.count;i++) {
int j=i;
NSInteger temp=[[arr objectAtIndex:i]integerValue];
while (j>0&&temp<[[arr objectAtIndex:j-1]integerValue]) {
[arr replaceObjectAtIndex:j withObject:[arr objectAtIndex:(j-1)]];
j--;
}
[arr replaceObjectAtIndex:j withObject:[NSNumber numberWithInteger:temp]];
}
NSLog(@"%@",arr);
}
5.4 希尔排序
-(void)xiEr{//希尔排序
NSMutableArray *arr=[NSMutableArray arrayWithArray:@[@"17",@"28",@"36",@"15",@"29",@"39"]];
NSInteger gap=arr.count/2;
while (gap>=1) {
for (NSInteger i=gap; i<arr.count; i++) {
NSInteger temp=[[arr objectAtIndex:i] integerValue];
NSInteger j=i;
while (j>=gap&&temp<[[arr objectAtIndex:(j-gap)] integerValue]) {\
[arr replaceObjectAtIndex:j withObject:[arr objectAtIndex:j-gap]];
j-=gap;
}
[arr replaceObjectAtIndex:j withObject:[NSNumber numberWithInteger:temp]];
}
gap=gap/2;
}
NSLog(@"%@",arr);
}
5.5 二分法查找
当数据量很大适宜采用该方法。 采用二分法查找时,数据需是排好序的。
基本思想:假设数据是按升序排序的,对于给定值x,从序列的中间位置开始比较,如果当前位置值等于x,则查找成功;若x小于当前位置值,则在数列的前半段 中查找;若x大于当前位置值则在数列的后半段中继续查找,直到找到为止。
- (NSInteger)BinarySearch:(NSArray *)array target:(id)key{//二分法查找
NSInteger left = 0;
NSInteger right = [array count] - 1;
NSInteger middle = [array count] / 2;
while (right >= left) {
middle = (right + left) / 2;
if (array[middle] == key) {
return middle;
}
if (array[middle] > key) {
right = middle - 1;
}
else if (array[middle] < key) {
left = middle + 1;
}
}
return -1;
}
5.6 快速排序
1. 从数列中挑出一个元素,称为 "基准"(pivot),
2. 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割之后,该基准是它的最后位置。这个称为分割(partition)操作。
3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递回的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递回下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
平均时间复杂度:O(n^2)
平均空间复杂度:O(nlogn) O(nlogn)~O(n^2)
- (NSMutableArray *)QuickSorkOC:(NSMutableArray *)array Count:(NSInteger)count{//快速排序
NSInteger i = 0;
NSInteger j = count - 1;
id pt = array[0];
if (count > 1) {
while (i < j) {
for (; j > i; --j) {
if (array[j] < pt) {
array[i++] = array[j];
break;
}
}
for (; i < j; ++i) {
if (array[i] > pt) {
array[j--] = array[i];
break;
}
}
array[i] = pt;
[self QuickSorkOC:array Count:i];
[self QuickSorkOC:array Count:count - i - 1];
}
}
return array;
}
5.7 归并排序
把序列分成元素尽可能相等的两半。
把两半元素分别进行排序。
把两个有序表合并成一个。
- (void)megerSortAscendingOrderSort:(NSMutableArray *)ascendingArr
{
NSMutableArray *tempArray = [NSMutableArray arrayWithCapacity:1];
for (NSNumber *num in ascendingArr) {
NSMutableArray *subArray = [NSMutableArray array];
[subArray addObject:num];
[tempArray addObject:subArray];
}
while (tempArray.count != 1) {
NSInteger i = 0;
while (i < tempArray.count - 1) {
tempArray[i] = [self mergeArrayFirstList:tempArray[i] secondList:tempArray[i + 1]];
[tempArray removeObjectAtIndex:i + 1];
i++;
}
}
NSLog(@"归并升序排序结果:%@", ascendingArr);
}
- (NSArray *)mergeArrayFirstList:(NSArray *)array1 secondList:(NSArray *)array2 {
NSMutableArray *resultArray = [NSMutableArray array];
NSInteger firstIndex = 0, secondIndex = 0;
while (firstIndex < array1.count && secondIndex < array2.count) {
if ([array1[firstIndex] floatValue] < [array2[secondIndex] floatValue]) {
[resultArray addObject:array1[firstIndex]];
firstIndex++;
} else {
[resultArray addObject:array2[secondIndex]];
secondIndex++;
}
}
while (firstIndex < array1.count) {
[resultArray addObject:array1[firstIndex]];
firstIndex++;
}
while (secondIndex < array2.count) {
[resultArray addObject:array2[secondIndex]];
secondIndex++;
}
return resultArray.copy;
}
5.8 基数排序
- (void)radixAscendingOrderSort:(NSMutableArray *)ascendingArr
{
NSMutableArray *buckt = [self createBucket];
NSNumber *maxnumber = [self listMaxItem:ascendingArr];
NSInteger maxLength = numberLength(maxnumber);
for (int digit = 1; digit <= maxLength; digit++) {
// 入桶
for (NSNumber *item in ascendingArr) {
NSInteger baseNumber = [self fetchBaseNumber:item digit:digit];
NSMutableArray *mutArray = buckt[baseNumber];
[mutArray addObject:item];
}
NSInteger index = 0;
for (int i = 0; i < buckt.count; i++) {
NSMutableArray *array = buckt[i];
while (array.count != 0) {
NSNumber *number = [array objectAtIndex:0];
ascendingArr[index] = number;
[array removeObjectAtIndex:0];
index++;
}
}
}
NSLog(@"基数升序排序结果:%@", ascendingArr);
}
1.冒泡排序
冒泡算法是一种基础的排序算法,这种算法会重复的比较数组中相邻的两个元素,如果一个元素比另一个元素大/小,那么就交换这两个元素的位置。重复一直比较到最后一个元素。
2:快速排序
设要排序的数组是mutableArray对象,首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一次快速排序。
1 ).设置两个变量i,j ,排序开始时i = 0,就j = mutableArray.count - 1;
2 ).设置数组的第一个值为比较基准数key,key = mutableArray.count[0];
3 ).因为设置key为数组的第一个值,所以先从数组最右边开始往前查找比key小的值。如果没有找到,j--继续往前搜索;如果找到则将mutableArray[i]和mutableArray[j]互换,并且停止往前搜索,进入第4步;
4 ).从i位置开始往后搜索比可以大的值,如果没有找到,i++继续往后搜索;如果找到则将mutableArray[i]和mutableArray[j]互换,并且停止往后搜索;
5 ).重复第3、4步,直到i == j(此时刚好执行完第三步或第四部),停止排序;
3:选择排序
选择排序:
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法。
一. 算法描述
选择排序:比如在一个长度为N的无序数组中,在第一趟遍历N个数据,找出其中最小的数值与第一个元素交换,第二趟遍历剩下的N-1个数据,找出其中最小的数值与第二个元素交换......第N-1趟遍历剩下的2个数据,找出其中最小的数值与第N-1个元素交换,至此选择排序完成。
4:插入排序也是一种比较直观的排序方式。可以以我们平常打扑克牌为例来说明,假设我们那在手上的牌都是排好序的,那么插入排序可以理解为我们每一次将摸到的牌,和手中的牌从左到右依次进行对比,如果找到合适的位置则直接插入。具体的步骤为:
从第一个元素开始,该元素可以认为已经被排序
取出下一个元素,在已经排序的元素序列中从后向前扫描
如果该元素小于前面的元素(已排序),则依次与前面元素进行比较如果小于则交换,直到找到大于该元素的就则停止;
如果该元素大于前面的元素(已排序),则重复步骤2
重复步骤2~4 直到所有元素都排好序 。
设数组为a[0…n-1]。
1. 初始时,a[0]自成1个有序区,无序区为a[1..n-1]。令i=1
2. 将a[i]并入当前的有序区a[0…i-1]中形成a[0…i]的有序区间。
3. i++并重复第二步直到i==n-1。排序完成。