05 (OC) 二叉树 深度优先遍历和广度优先遍历

总结深度优先与广度优先的区别

 

1、区别

       1） 二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

       2） 深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：

• 先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树。
• 中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。
• 后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。

        广度优先遍历：又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。　　　

     3）深度优先搜素算法：不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢。

          广度优先搜索算法：保留全部结点，占用空间大； 无回溯操作(即无入栈、出栈操作)，运行速度快。

          通常 深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。

所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。 　

          广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。

但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些

    4）深度优先遍历：用时间换空间。

　　 广度优先遍历：用空间换时间。

2.二叉树的遍历

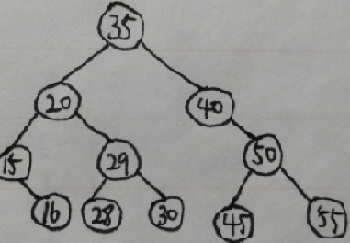
先序遍历（递归）：35 20 15 16 29 28 30 40 50 45 55 
中序遍历（递归）：15 16 20 28 29 30 35 40 45 50 55 
后序遍历（递归）：16 15 28 30 29 20 45 55 50 40 35 
先序遍历（非递归）：35 20 15 16 29 28 30 40 50 45 55 
中序遍历（非递归）：15 16 20 28 29 30 35 40 45 50 55 
后序遍历（非递归）：16 15 28 30 29 20 45 55 50 40 35 
广度优先遍历：35 20 40 15 29 50 16 28 30 45 55