053*:bitMap
一:bitMap:
所谓的Bit-map就是用一个bit位来标记某个元素对应的Value, 而Key即是该元素。由于采用了Bit为单位来存储数据,因此在存储空间方面,可以大大节省。 如果说了这么多还没明白什么是Bit-map,那么我们来看一个具体的例子,假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复)。 那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0 然后遍历这5个元素,首先第一个元素是4,那么就把4对应的位置为1(可以这样操作 p+(i/8)|(0×01<<(i%8)) 当然了这里的操作涉及到Big-ending和Little-ending的情况,这里默认为Big-ending),因为是从零开始的,所以要把第五位置为1。 然后再处理第二个元素7,将第八位置为1,,接着再处理第三个元素,一直到最后处理完所有的元素,将相应的位置为1。 然后我们现在遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的。 其实就是把计数排序用的统计数组的每个单位缩小成bit级别的布尔数组
这就是Bit-map的基本思想。Bit-map算法利用这种思想处理大量数据的排序、查询以及去重。
二、应用与代码
如果BitMap仅仅是这个特点,我觉得还不是它的优雅的地方,接下来继续欣赏它的魅力所在。下面的计算思想其实就是针对bit的逻辑运算得到,类似这种逻辑运算的应用场景可以用于权限计算之中。
再看代码之前,我们先搞清楚一个问题,一个数怎么快速定位它的索引号,也就是说搞清楚byte[index]的index是多少,position是哪一位。举个例子吧,例如add(14)。14已经超出byte[0]的映射范围,在byte[1]范围之类。那么怎么快速定位它的索引呢。如果找到它的索引号,又怎么定位它的位置呢。Index(N)代表N的索引号,Position(N)代表N的所在的位置号。
Index(N) = N/8 = N >> 3;
Position(N) = N%8 = N & 0x07;
1:add(int num) 位或运算
1<<左移动num位,和bit[0]进行 位或运算
你要向bitmap里add数据该怎么办呢,不用担心,很简单,也很神奇。
上面已经分析了,add的目的是为了将所在的位置从0变成1.其他位置不变.
这里有个问题,我们怎么把一个数放进去呢?例如,想把5这个数字放进去,怎么做呢?
首先,5/32=0,5%32=5,也是说它应该在tmp[0]的第5个位置,那我们把1向左移动5位,然后按位或
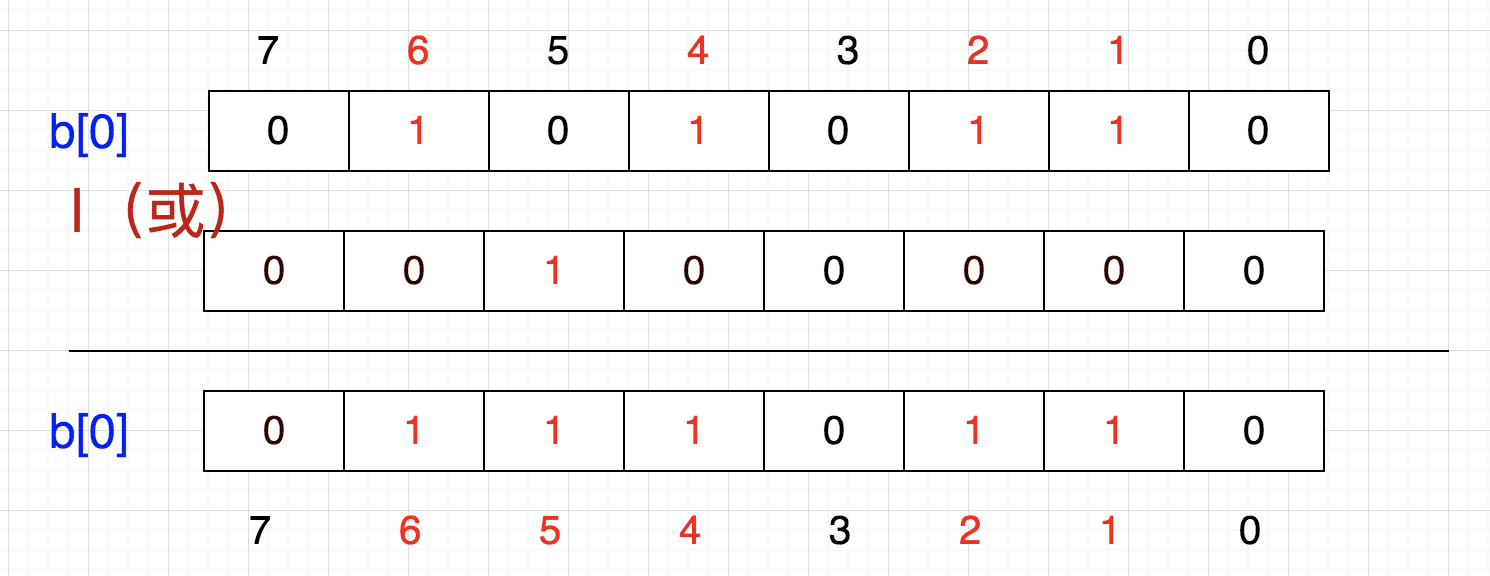
换成二进制就是

这就相当于 86 | 32 = 118
86 | (1<<5) = 118
b[0] = b[0] | (1<<5)
也就是说,要想插入一个数,将1左移带代表该数字的那一位,然后与原数进行按位或操作
化简一下,就是 86 + (5/8) | (1<<(5%8))
因此,公式可以概括为:p + (i/8)|(1<<(i%8)) 其中,p表示现在的值,i表示待插入的数
2:清除 位与 运算
以上是添加,那如果要清除该怎么做呢?
还是上面的例子,假设我们要6移除,该怎么做呢?
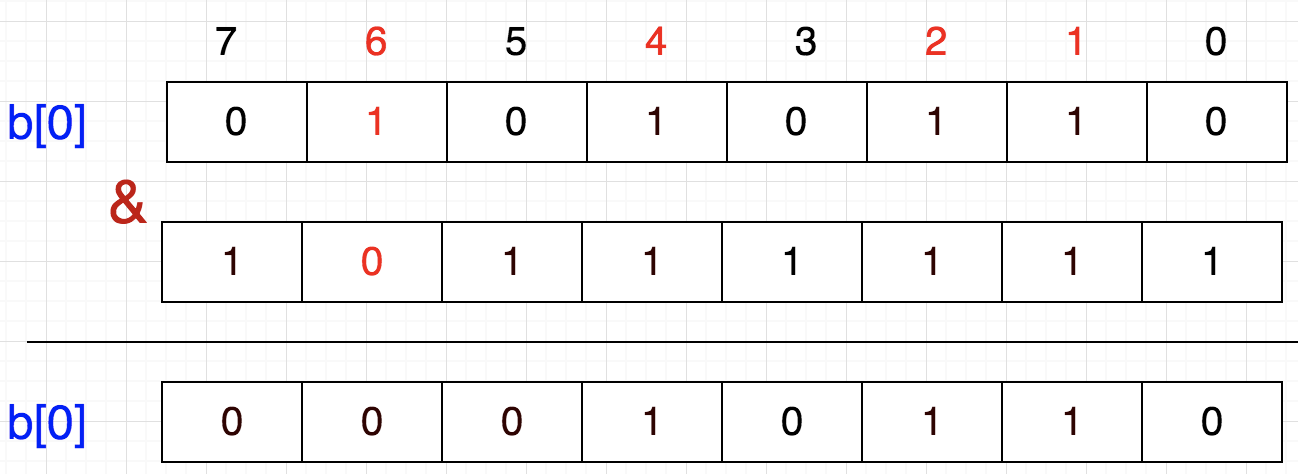
从图上看,只需将该数所在的位置为0即可
1:1左移6位,就到达6这个数字所代表的位,
2:然后按位取反,
3:最后与原数按位与,这样就把该位置为0了
b[0] = b[0] & (~(1<<6))
b[0] = b[0] & (~(1<<(i%8)))
3:查找
前面我们也说了,每一位代表一个数字,1表示有(或者说存在),0表示无(或者说不存在)。通过把该为置为1或者0来达到添加和清除的小伙,那么判断一个数存不存在就是判断该数所在的位是0还是1
假设,我们想知道3在不在,那么只需判断 b[0] & (1<<3) 如果这个值是0,则不存在,如果是1,就表示存在
三: Bitmap有什么用
大量数据的快速排序、查找、去重
大量数据的快速排序、查找、去重
快速排序
假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复),我们就可以采用Bit-map的方法来达到排序的目的。
要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0,然后将对应位置为1。
最后,遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的,时间复杂度O(n)。
优点:
- 运算效率高,不需要进行比较和移位;
- 占用内存少,比如N=10000000;只需占用内存为N/8=1250000Byte=1.25M
缺点:
- 所有的数据不能重复。即不可对重复的数据进行排序和查找。
- 只有当数据比较密集时才有优势
快速去重
20亿个整数中找出不重复的整数的个数,内存不足以容纳这20亿个整数。
首先,根据“内存空间不足以容纳这05亿个整数”我们可以快速的联想到Bit-map。下边关键的问题就是怎么设计我们的Bit-map来表示这20亿个数字的状态了。其实这个问题很简单,一个数字的状态只有三种,分别为不存在,只有一个,有重复。因此,我们只需要2bits就可以对一个数字的状态进行存储了,假设我们设定一个数字不存在为00,存在一次01,存在两次及其以上为11。那我们大概需要存储空间2G左右。
接下来的任务就是把这20亿个数字放进去(存储),如果对应的状态位为00,则将其变为01,表示存在一次;如果对应的状态位为01,则将其变为11,表示已经有一个了,即出现多次;如果为11,则对应的状态位保持不变,仍表示出现多次。
最后,统计状态位为01的个数,就得到了不重复的数字个数,时间复杂度为O(n)。
快速查找
这就是我们前面所说的了,int数组中的一个元素是4字节占32位,那么除以32就知道元素的下标,对32求余数(%32)就知道它在哪一位,如果该位是1,则表示存在。
小结&回顾
Bitmap主要用于快速检索关键字状态,通常要求关键字是一个连续的序列(或者关键字是一个连续序列中的大部分), 最基本的情况,使用1bit表示一个关键字的状态(可标示两种状态),但根据需要也可以使用2bit(表示4种状态),3bit(表示8种状态)。
Bitmap的主要应用场合:表示连续(或接近连续,即大部分会出现)的关键字序列的状态(状态数/关键字个数 越小越好)。
32位机器上,对于一个整型数,比如int a=1 在内存中占32bit位,这是为了方便计算机的运算。但是对于某些应用场景而言,这属于一种巨大的浪费,因为我们可以用对应的32bit位对应存储十进制的0-31个数,而这就是Bit-map的基本思想。Bit-map算法利用这种思想处理大量数据的排序、查询以及去重。
补充1
在数字没有溢出的前提下,对于正数和负数,左移一位都相当于乘以2的1次方,左移n位就相当于乘以2的n次方,右移一位相当于除2,右移n位相当于除以2的n次方。
<< 左移,相当于乘以2的n次方,例如:1<<6 相当于1×64=64,3<<4 相当于3×16=48
>> 右移,相当于除以2的n次方,例如:64>>3 相当于64÷8=8
^ 异或,相当于求余数,例如:48^32 相当于 48%32=16
补充2
不使用第三方变量,交换两个变量的值
// 方式一 2 a = a + b; 3 b = a - b; 4 a = a - b; 5 6 // 方式二 7 a = a ^ b; 8 b = a ^ b; 9 a = a ^ b;
引用:



