25*:排序算法:总结 (1、冒泡排序:2:选择排序:3、插入排序:4、希尔排序:5、堆排序:6、归并排序:7、快速排序:)
问题
目录
1、冒泡排序:未排序区间两两交换找到最大值,排在最后,形成有序区间。稳定
2:选择排序:从未排序区间找最小元素,和排序区间的最后一个元素交换位置。
3、插入排序:从未排序区间依次取出元素插入到排序区间的适当位置。稳定
4、希尔排序:缩小增量排序
5、堆排序:完全二叉树大堆顶,交互堆顶和最后元素,找到最大元素。循环在未排序区间找到最大元素,依次排序。
6、归并排序:两两分而治之。稳定
7、快速排序:分区值,分而治之
预备
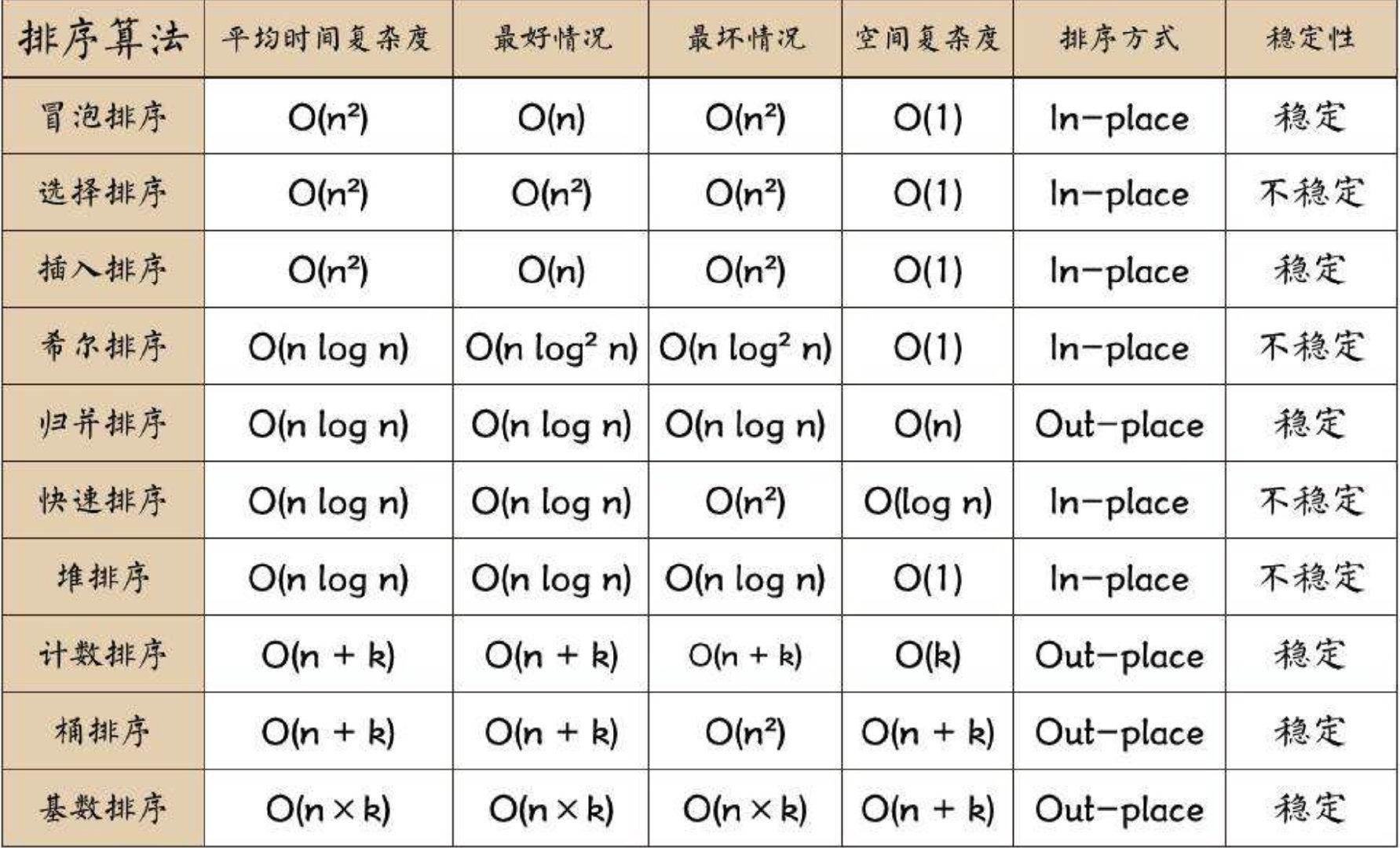
正文
1、冒泡排序:未排序区间两两交换找到最大值,排在最后,形成有序区间。稳定
原理:
1:这种算法会重复的比较数组中相邻的两个元素,如果一个元素比另一个元素大(小),那么就交换这两个元素的位置。重复这一比较直至最后一个元素。每一趟比较都能找出未排序元素中最大或者最小的那个数字。这就如同水泡从水底逐个飘到水面一样。冒泡排序是一种时间复杂度较高,效率较低的排序方法。
2:这一比较会重复n-1趟,每一趟比较n-j次,j是已经排序好的元素个数。
每一趟会找到最大(或者最小)的数据,排成有序区间,之后在没有排序区间的n-j中找最大或者最小数据再排列。
时间复杂度:O(n^2),优化后可能达到O(n),但会增加空间复杂度
-(void)bubbleSequence:(NSMutableArray *)arr { //普通排序-交换次数较多 for (int i = 0; i < arr.count; ++i) { for (int j = 0; j < arr.count-1-i; ++j) { if ([arr[j+1] intValue] < [arr[j] intValue]) {
[arr exchangeObjectAtIndex:j withObjectAtIndex:j+1]; } } } //优化后算法-从最后一个开始排序 for (int i = 0; i <arr.count; ++i) { bool flag=false; //遍历数组的每一个`索引`(不包括最后一个,因为比较的是j+1) for (int j = (int)arr.count-1; j >i; --j) { //根据索引的`相邻两位`进行`比较` if ([arr[j-1] intValue] > [arr[j] intValue]) { flag = true; [arr exchangeObjectAtIndex:j withObjectAtIndex:j-1]; } } if (!flag) { break;//没发生交换直接退出,说明是有序数组 } } }
2:选择排序:从未排序区间找最小元素,和排序区间的最后一个元素交换位置。
原理:
选择排序分已排序区间和未排序区间。从第一个元素开始,依次查找对比,找到最小的元素与第一个元素交换,再从第二个元素(没有排序区间的第一个元素)开始找后面元素的最小值与第二个元素交换,以此类推,直到整个数组有序。
时间复杂度:O(n^2)
- (void)selectionAscendingOrderSortWithArray:(NSMutableArray *)ascendingArr { int index = 0;//记录找到的关键字下标 for (int i = 0; i < arr.count - 1; i++) { index = i; for (int j = i + 1; j < arr.count; j++) { if ([arr[index] integerValue] < [arr[j]integerValue]) { //如果有比当前index值大的值,则记录次下标 index = j;//记录最大值(最小值)的下标 } } if (i != index) { //若index不等于i,说明找到最大值,交换 [arr exchangeObjectAtIndex:i withObjectAtIndex:index]; } NSLog(@"%@",arr); }
3、插入排序:从未排序区间依次取出元素插入到排序区间的适当位置。稳定
时间复杂度:O(n^2)
#pragma mark - 插入升序排序 - (void)insertionAscendingOrderSort:(NSMutableArray *)ascendingArr { for (NSInteger i = 1; i < ascendingArr.count; i ++) { NSInteger temp = [ascendingArr[i] integerValue]; for (NSInteger j = i - 1; j >= 0 && temp < [ascendingArr[j] integerValue]; j --) { ascendingArr[j + 1] = ascendingArr[j]; ascendingArr[j] = [NSNumber numberWithInteger:temp]; } } NSLog(@"插入升序排序结果:%@",ascendingArr); }
4、希尔排序:缩小增量排序
原理:
1:使用分组的方式,分组策略使用一个递减序列,每组依然使用插入排序算法进行组内排序。即局部有序
2:一直分组下去,直到分组为1,组内就是全部元素了,分组越少,组内成员就越多,局部有序元素就越多,即全部有序,全排序。
时间复杂度:O(n logn)
//起始间隔值gap设置为总数的一半,直到gap==1结束 -(void)shellSort:(NSMutableArray *)list{ int gap = (int)list.count / 2; while (gap >= 1) { for(int i = gap ; i < [list count]; i++){ NSInteger temp = [[list objectAtIndex:i] intValue]; int j = i; while (j >= gap && temp < [[list objectAtIndex:(j - gap)] intValue]) { [list replaceObjectAtIndex:j withObject:[list objectAtIndex:j-gap]]; j -= gap; } [list replaceObjectAtIndex:j withObject:[NSNumber numberWithInteger:temp]]; } gap = gap / 2; } }
5、堆排序:完全二叉树大堆顶,交互堆顶和最后元素,找到最大元素。循环在未排序区间找到最大元素,依次排序。
原理
1: 从下往上,从右往左的顺序查找每个非叶子结点,对比子结点,与最大结点交换位置,交换的新位置再与其子结点比较、移动,遍历后最终找到最大值,形成一个大顶堆(小顶堆也行)。
2:把堆顶和最后的元素交换位置,排除最后的位置,重复1步骤,找到遍历后的最大值,放到倒数第二的位置,依次直到结束。
时间复杂度:O(n logn)
- (void)heapSort:(NSMutableArray *)list { NSInteger i ,size; size = list.count; //找出最大的元素放到堆顶 for (i= list.count/2; i>=0; i--) { [self createBiggesHeap:list withSize:size beIndex:i]; } while(size > 0){ [list exchangeObjectAtIndex:size-1 withObjectAtIndex:0]; //将根(最大) 与数组最末交换 size -- ;//树大小减小 [self createBiggesHeap:list withSize:size beIndex:0]; } NSLog(@"%@",list); } - (void)createBiggesHeap:(NSMutableArray *)list withSize:(NSInteger) size beIndex:(NSInteger)element { NSInteger lchild = element *2 + 1,rchild = lchild+1; //左右子树 while (rchild < size) { //子树均在范围内 if (list[element]>=list[lchild] && list[element]>=list[rchild]) return; //如果比左右子树都大,完成整理 if (list[lchild] > list[rchild]) { //如果左边最大 [list exchangeObjectAtIndex:element withObjectAtIndex:lchild]; //把左面的提到上面 element = lchild; //循环时整理子树 }else{//否则右面最大 [list exchangeObjectAtIndex:element withObjectAtIndex:rchild]; element = rchild; } lchild = element * 2 +1; rchild = lchild + 1; //重新计算子树位置 } //只有左子树且子树大于自己 if (lchild < size && list[lchild] > list[element]) { [list exchangeObjectAtIndex:lchild withObjectAtIndex:element]; } }
6、归并排序:两两分而治之。稳定
原理
1:分治,分而治之,将原数组一直拆分成左右两个小数组,直至小数组元素个数为1,
2:然后每两个小数组进行有序归并,直至归并成一个完整的数组,从而达到整个数组有序的目的。由于每两个小的数组都是有序的,所以在每次合并的时候是很快的。合并的时候用插入排序形成有序区间。
时间复杂度:O(n logn)
- (void)megerSortAscendingOrderSort:(NSMutableArray *)ascendingArr { //tempArray数组里存放ascendingArr个数组,每个数组包含一个元素 NSMutableArray *tempArray = [NSMutableArray arrayWithCapacity:1]; for (NSNumber *num in ascendingArr) { NSMutableArray *subArray = [NSMutableArray array]; [subArray addObject:num]; [tempArray addObject:subArray]; } //开始合并为一个数组 while (tempArray.count != 1) { NSInteger i = 0; while (i < tempArray.count - 1) { tempArray[i] = [self mergeArrayFirstList:tempArray[i] secondList:tempArray[i + 1]]; [tempArray removeObjectAtIndex:i + 1]; i++; } } NSLog(@"归并升序排序结果:%@", tempArray[0]); } - (NSArray *)mergeArrayFirstList:(NSArray *)array1 secondList:(NSArray *)array2 { NSMutableArray *resultArray = [NSMutableArray array]; NSInteger firstIndex = 0, secondIndex = 0; while (firstIndex < array1.count && secondIndex < array2.count) { if ([array1[firstIndex] floatValue] < [array2[secondIndex] floatValue]) { [resultArray addObject:array1[firstIndex]]; firstIndex++; } else { [resultArray addObject:array2[secondIndex]]; secondIndex++; } } while (firstIndex < array1.count) { [resultArray addObject:array1[firstIndex]]; firstIndex++; } while (secondIndex < array2.count) { [resultArray addObject:array2[secondIndex]]; secondIndex++; } return resultArray.copy; }
7、快速排序:分区值,分而治之
原理:
1:每次选一个pivot(分区值),其他数依次和 pivot 比较,大的放右边小的放左边,
2:然后再对左边和右边的两组数,分别选出pivot,重复比较,大的放左边,小的放右边;重复步骤,直到最后都变成单个元素,整个数组就成了有序的序列。
时间复杂度:O(n logn)
-(void)quickSequence:(NSMutableArray *)arr andleft:(int)left andright:(int)right { if (left >= right) {//如果数组长度为0或1时返回 return ; } int key = [arr[left] intValue]; int i = left; int j = right; while (i<j){ while (i<j&&[arr[j] intValue]>=key) { j--; } arr[i] = arr[j]; while (i<j&&[arr[i] intValue]<=key) { i++; } arr[j] = arr[i]; } arr[i] = [NSString stringWithFormat:@"%d",key]; [self quickSequence:arr andleft:left andright:i-1]; [self quickSequence:arr andleft:i+1 andright:right]; }
注意



