24*:排序算法7:快速排序(分区值,分而治之)
问题
目录
预备
快排利用了分治的思想,分而治之,分治算法的基本思想是将一个规模为N的问题,分解成K个规模较小的子问题,这些子问题相互独立且问题性质相同。
求解出子问题的解,合并得到原问题的解。拆分问题总不可能手脚并用一个个拆分,因此分治算法大多采用递归实现。
正文
快速排序
1:算法描述
对A[p....r]进行快速排序的分治过程:
分解:选择一个枢轴(pivot)元素划分数组。将数组 A[p..r] 划分为两个子数组(可能为空) A[p..q-1] 和 A[q+1..r],使得 A[q] 大于等于A[p..q-1] 中的每个元素,小于 A[q+1..r] 中的每个元素。计算下标 q 的值也是划分过程的一部分;求解:通过递归调用快速排序,对子数组 A[p..q-1] 和 A[q+1..r] 分别排序;合并:子数组在原地排序,故无需合并操作,数组 A[p...r] 已经有序。
首先,每次重复,pivot 一定会有序,这点和冒泡排序很像,冒泡排序也是每次遍历冒泡,都会有一个元素排序正确;再者,快排也是两两比较,交换位置,和冒泡排序也是相似的,快排的核心交换代码和冒泡神似,这些点可说快速排序是冒泡排序的变种。
3:动图演示
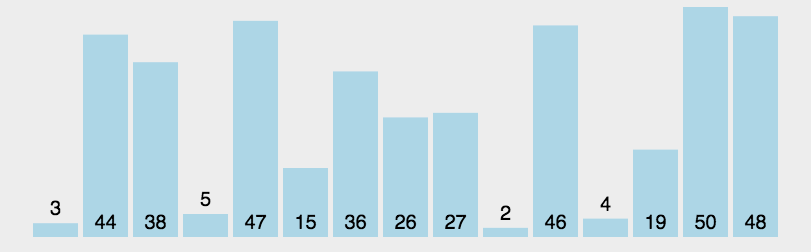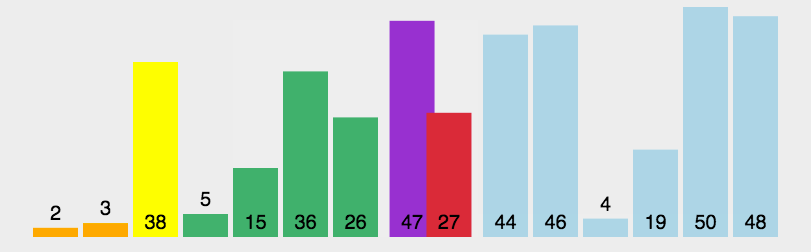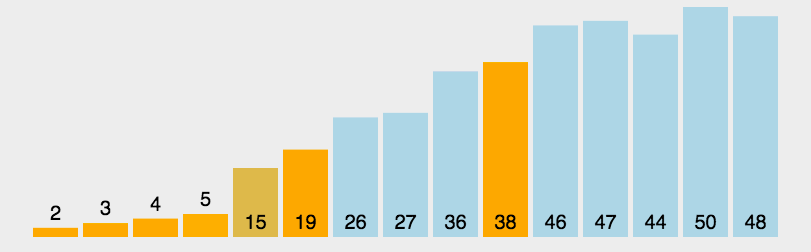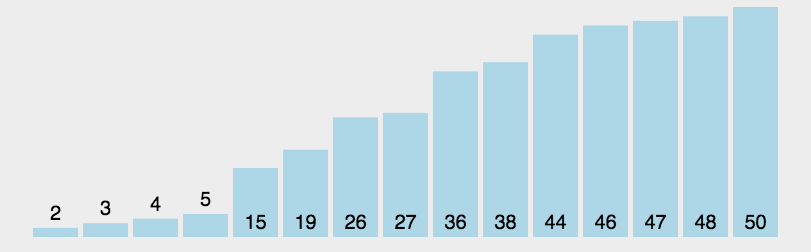
-
明黄色代表此次遍历选定的 pivot,每次选数组第一个数作为 pivot,本数组 pivot 分别为3,38,19,4,26,27,46,47,50;
-
暗黄色代表已经排好序的元素;
-
绿色代表比基准值 pivot 小的数据,紫色代表比基准值 pivot 大的数据,绿色子数组和紫色子数组有会进行切割数组排序,直到子数组只有一个元素为止;
-
每次遍历过后,至少有一个元素会是有序的, pivot 元素一定有序。
4:图解分析:
图解还是用上面数组里的数据做分析,动图里面元素太多了。
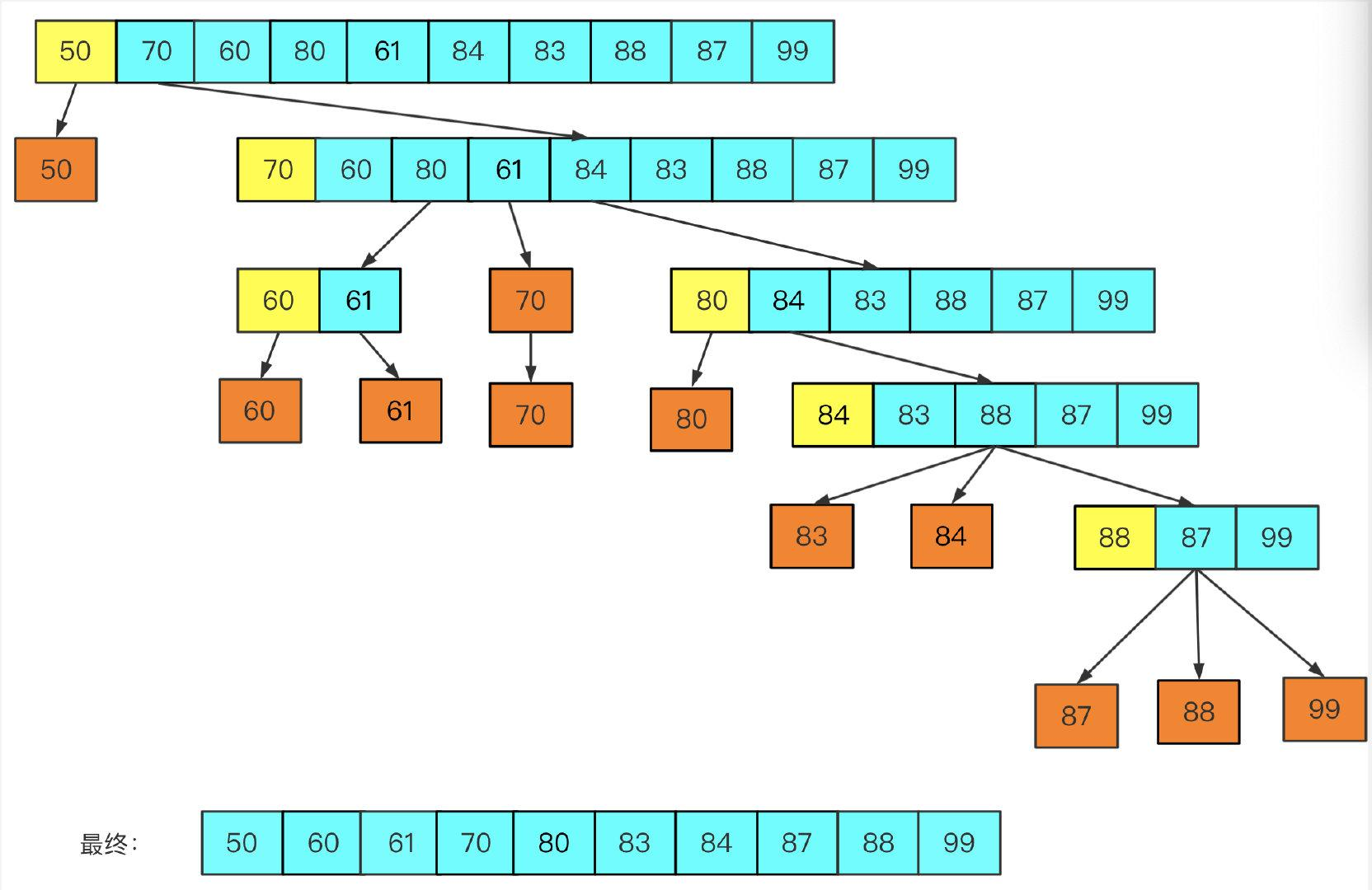
明黄色代表此分组选定的 pivot, 暗黄色代表已经排好序的,当分组内只有一个元素不需要再排序。
可知,每次遍历之后,pivot 是一定有序的,其他元素如果组内只剩下一个元素也有序。
5:代码实现
-
每次取数组第一个元素作为基准值 pivot,设定数组基准值 pivot 右边第一个数为mark用来存储比 pivot 小的元素,遍历数组;
-
元素大于 pivot,正常,继续遍历;
-
遍历元素小于 pivot,将此元素放入mark位置,即此元素与mark所指元素互换,选择mark后面一个元素位置继续存储小于pivot值的元素;
-
一趟遍历下来,mark存储了所有比第一个元素pivot小的元素,将pivot与mark最后一个元素交换,使得pivot去中间,pivot左边的都比它小,右边的都比它大
public class QuickSort { public static int[] quickSort(int[] arr) { return sort(arr, 0, arr.length-1); } public static int[] sort(int[] arr, int left, int right) { // 递归终止条件,子数组长度为1 if (left >= right) { return arr; } //获取中轴元素所处的位置,即 pivot 的值 int pivot = partition(arr, left, right); //切割,递归先排左边数组 arr = sort(arr, left, pivot - 1); //切割,递归排好右边数组 arr = sort(arr, pivot + 1, right); return arr; } private static int partition(int[] arr, int left, int right) { // pivot 选取数组第一个元素 int pivot = arr[left]; // mark 初始选取 pivot 右边第一个元素,存储小于 pivot 的元素, mark 最后指的元素就是小于 pivot 的数组最后一个值 int mark = left + 1; for (int i = mark; i <= right; i++) { // 如果遍历的元素小于 pivot 元素,和 mark 元素交换 if (arr[i] < pivot) { int temp = arr[i]; arr[i] = arr[mark]; arr[mark] = temp; // mark 元素向右挪一位 mark ++; } } // 交换到最后 mark 多加了1,需减去; mark -= 1; // 如果left==mark,表示没有交换过,没有比pivot小的值,这个pivot即为一组,直接返回 mark if (left < mark) { // pivot 所指第一个元素和 mark元素交换,即pivot元素和小于pivot的最后一个元素互换,使得 pivot 左边元素全部小于pivot arr[left] = arr[mark]; arr[mark] = pivot; } return mark; } }
稳定性分析
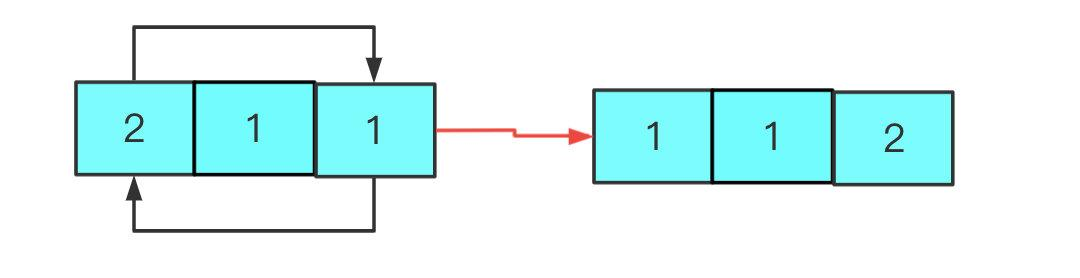
不稳定。
还是3 1 1 2数组分析,第一次分区 [2,1,1], [3],第二次分区[1,1,2],[3],这里两个 1 就调换了位置
时间复杂度分析
最好的情况下,如果每次分区操作,都能正好把数组分成大小接近相等的两个小区间,用递归树来表示如下图:
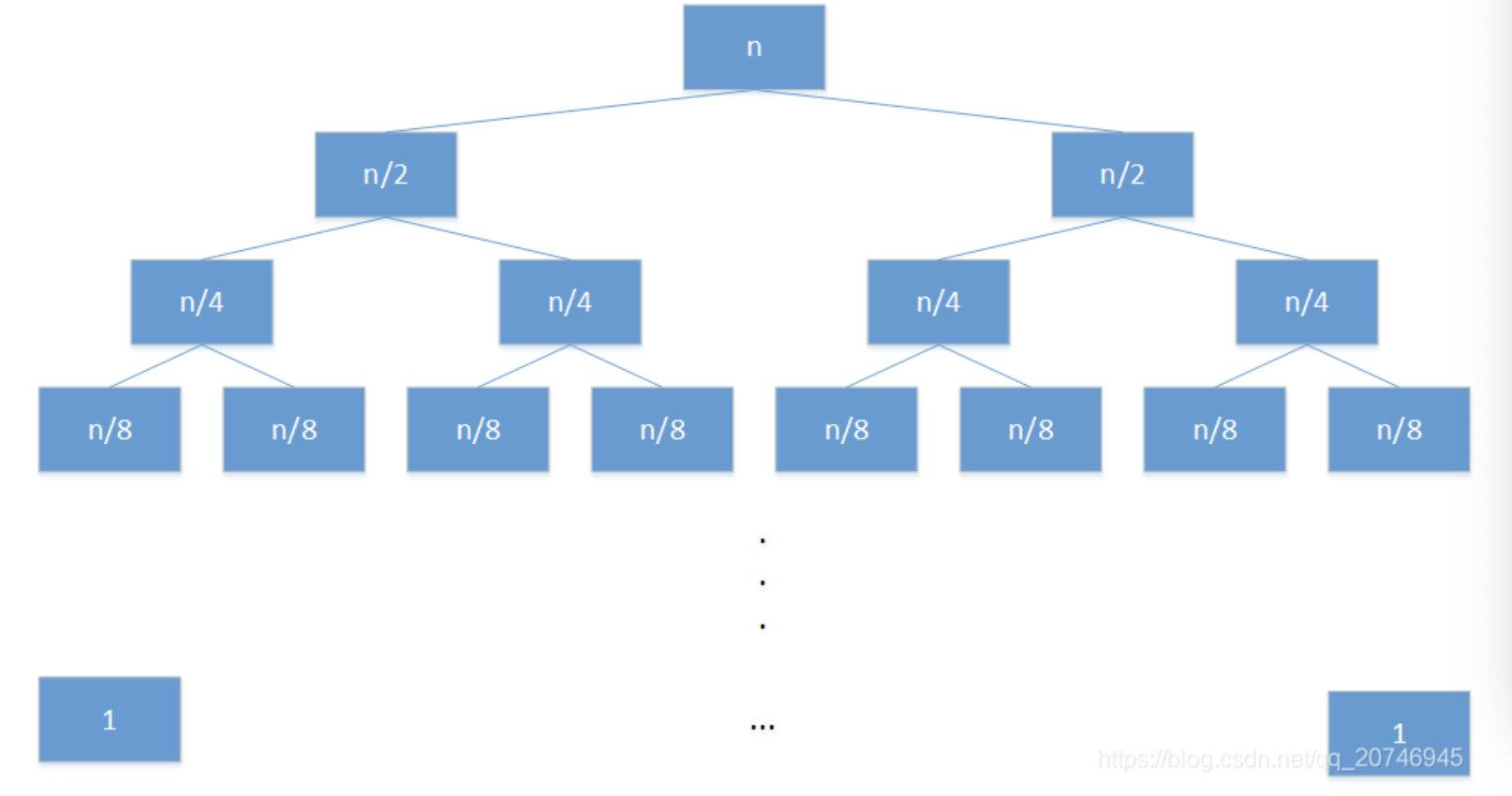
第1层是n次, 第2层有2次递归,每次n/2次,共n次操作, 第3层有4次递归,每次n/4次,共n次操作, …… (最后一层)第k层有k次递归,每次n/2^(k-1)次,共n次操作 由于递归结束的条件是只有一个元素,所以这里的**n/2^(k-1)=1** => **k=logn+1** 即递归树的**深度为logn** 时间复杂度=每层的操作次数*树的深度=nlogn 即:O(nlogn);
时间复杂度:最差O(n^2),平均O(nlogn)
空间复杂度:O(nlogn)
-(void)quickSequence:(NSMutableArray *)arr andleft:(int)left andright:(int)right { if (left >= right) {//如果数组长度为0或1时返回 return ; } int key = [arr[left] intValue]; int i = left; int j = right; while (i<j){ while (i<j&&[arr[j] intValue]>=key) { j--; } arr[i] = arr[j]; while (i<j&&[arr[i] intValue]<=key) { i++; } arr[j] = arr[i]; } arr[i] = [NSString stringWithFormat:@"%d",key]; [self quickSequence:arr andleft:left andright:i-1]; [self quickSequence:arr andleft:i+1 andright:right]; }
注意



