23*:排序算法6:归并排序(两两分而治之。稳定)
问题
目录
预备
归并排序在数据量大且数据递增或递减连续性好的情况下,效率比较高,且是O(nlogn)复杂度下唯一一个稳定的排序,致命缺点就是空间复杂度O(n)比较高。实际上,工程里面的算法都是结合这些算法的优缺点来使用的,例如Java1.8源码中Arrays.sort()排序函数,就同时使用了插入排序,快速排序和归并排序:
- 在元素小于 47 的时候用插入排序;
- 大于 47 小于 286 用双轴快排;
- 大于 286 用 timsort 归并排序,并在 timsort 中记录数据的连续的有序段的的位 置,若有序段太多,也就是说数据近乎乱序,则用双轴快排;
- 上面提到的快排的递归调用的过程中,若排序的子数组数据数量小,用插入排序。
归并排序使用的就是分治思想,这个思想我在上一篇讲希尔排序的时候也提到过,归并排序是高效算法设计中最典型的一个了。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决,小的子问题解决了,大问题也就解决了。分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。
正文
归并排序
归并排序有两种,自顶向下和自底向上。
1:算法描述
先拆分再归并,将一个大的无序数组,拆分成两个,先处理左边再处理右边(可以对比二叉树前序遍历),一直递归拆分直至只有一个元素然后两两进行归并(插入排序),一直重复这个过程直至合并完所有的子数组得到有序的完整数组,过程如下图。
自顶向下归并:
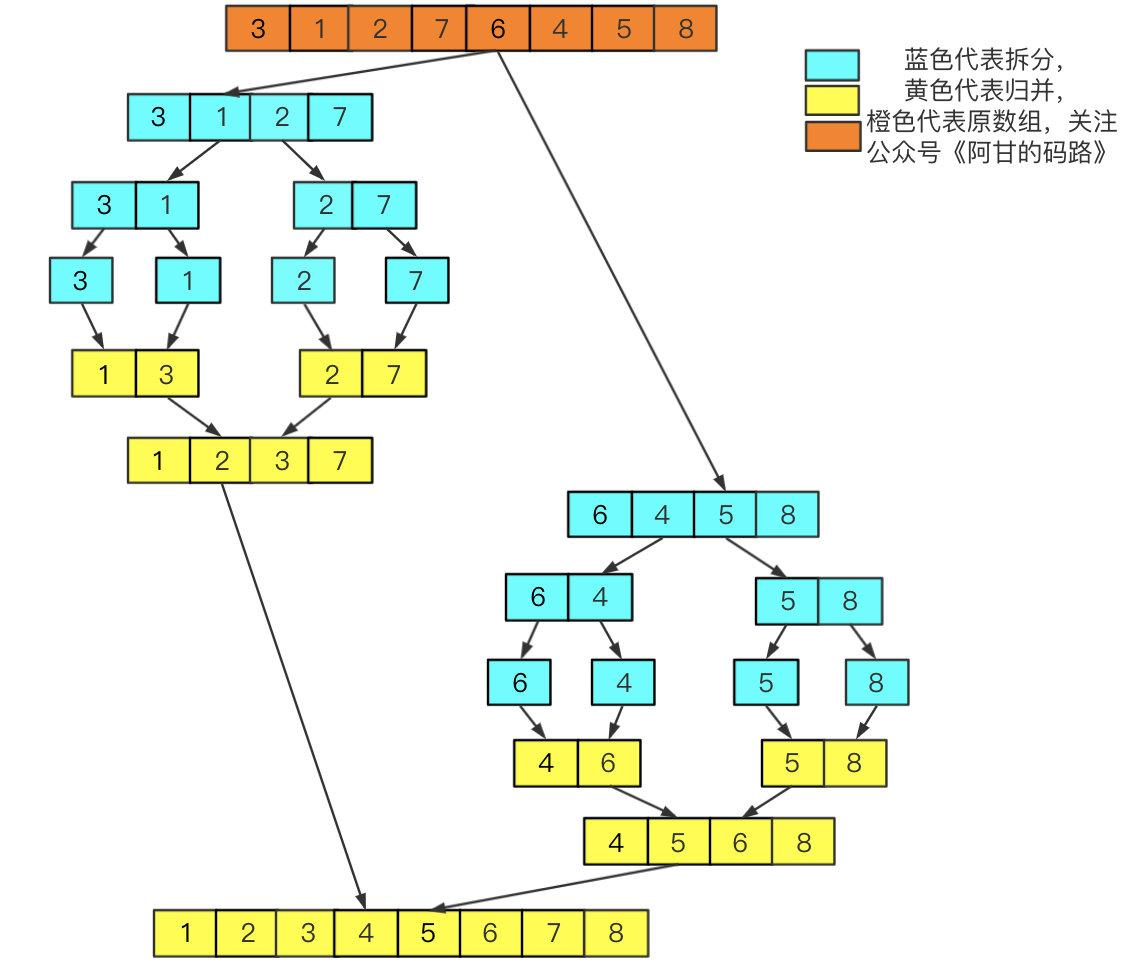
自底向上归并:
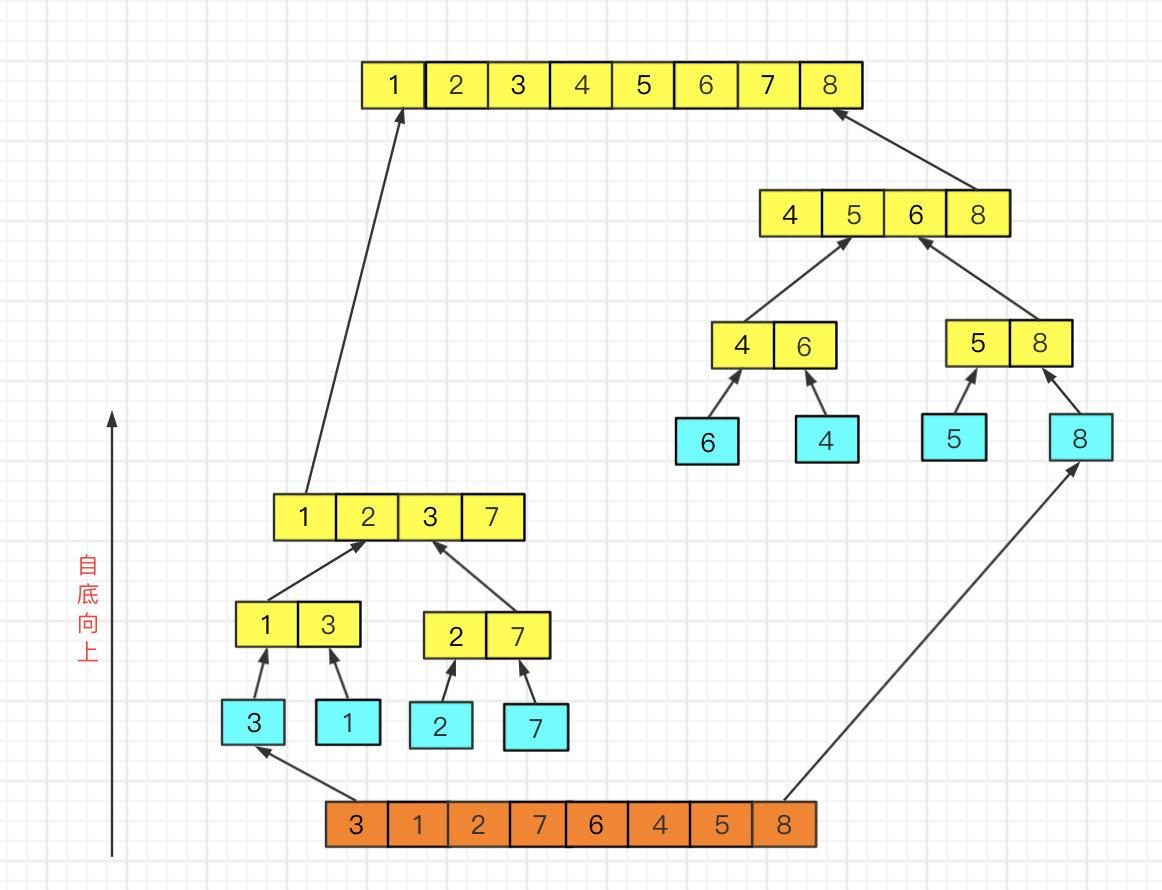
2:算法思想
分治,分而治之,将原数组一直拆分成左右两个小数组,直至小数组元素个数为1,然后每两个小数组进行有序归并,直至归并成一个完整的数组,从而达到整个数组有序的目的。由于每两个小的数组都是有序的,所以在每次合并的时候是很快的。
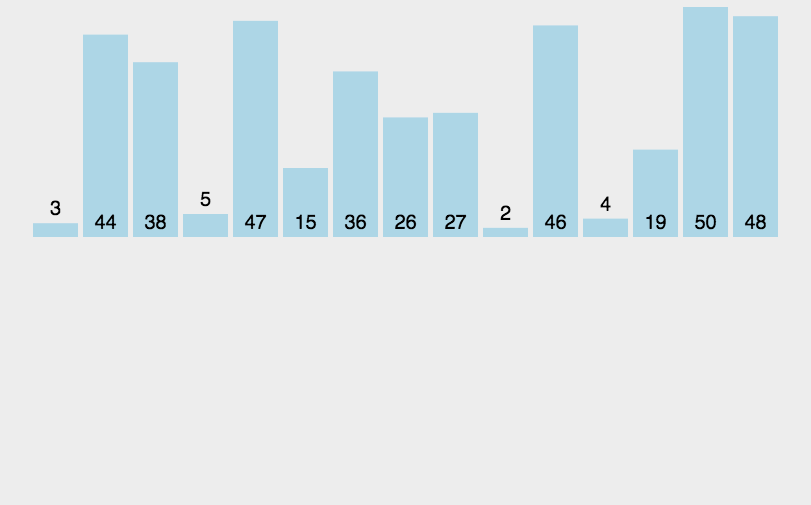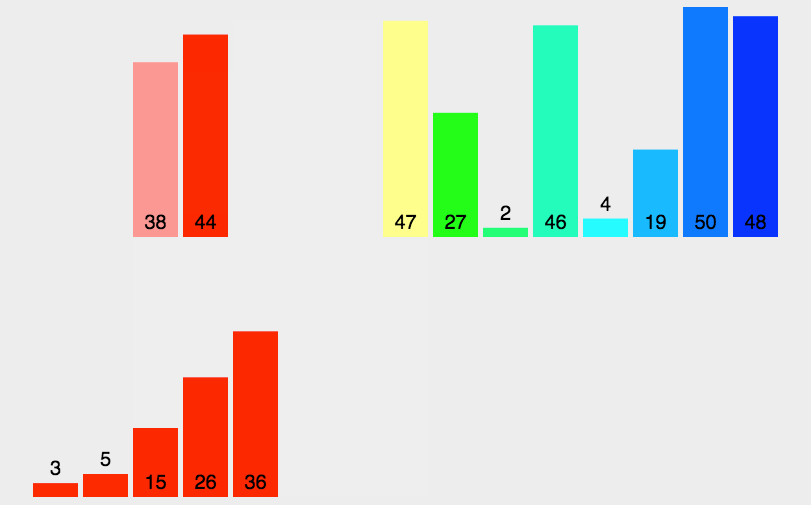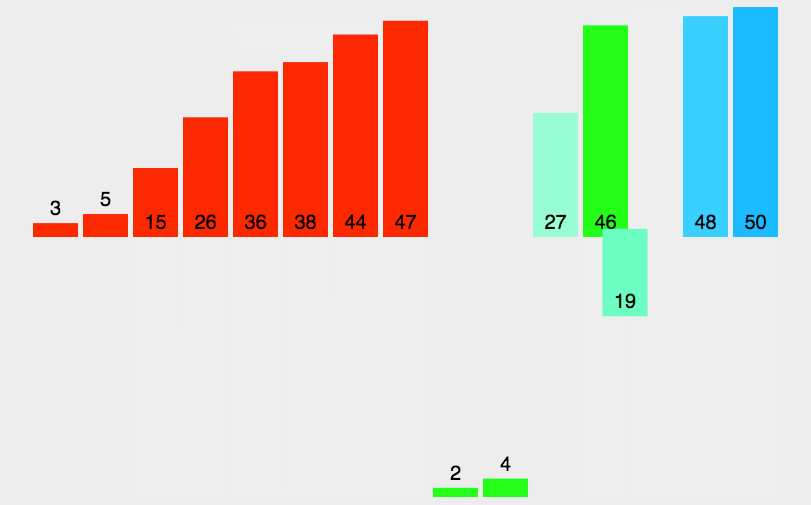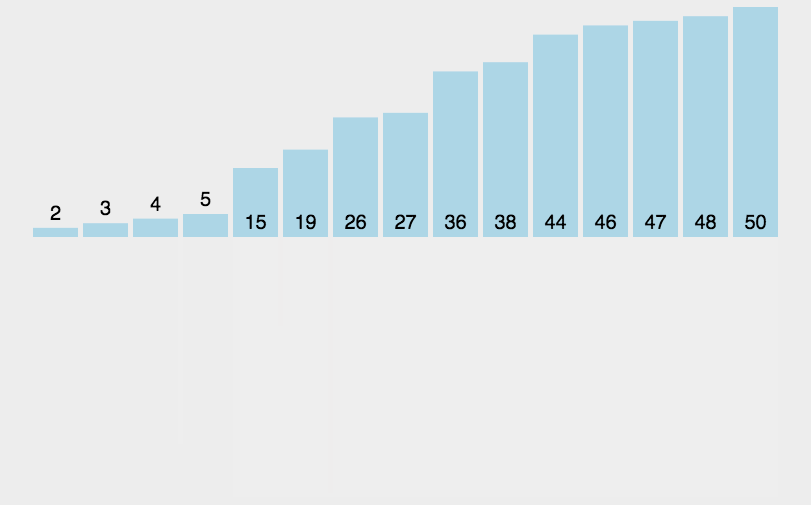
拆分都是无脑二分,直接用个递归拆分就可以,灵魂是归并过程,下面来图解下归并过程:
由图中黄色部分可知,实现归并时将两个不同的有序数组归并到第三个数组中了,这里借助了第三个数组。但是,我们需要进行很多次归并,这样每次归并时都创建一个新数组来存储排序结果就会浪费空间,因此我们可以只创建一个和原数组同样大小的数组作为辅助空间。但是这个数组不是用于存放归并后的结果,而是存放归并前的结果,然后将归并后的结果一个个从小到大放入原来的数组中,可知归并排序还需要一个n大小空间内存进行辅助排序,空间复杂度O(n)。如果原数组很大那么需要双倍的内存空间来排序,这里就是我上面提到的归并排序的最大的弊端,因为上几篇提到的排序那都是在原数组上面进行操作就可以的呢。
如果上面的拆分和归并都理解了的话,写代码应该不难,静下心来写即可,看代码的理解的时候,如果对递归过程不好理解,可以在idea里面对代码进行打断点看全部的过程。
4:代码
自顶向下,使用递归:
public class MergeSort { public static int[] mergeSort(int[] arr) { int[] arr_temp = Arrays.copyOf(arr, arr.length); sort(arr, arr_temp, 0, arr.length - 1); return arr; } public static void sort(int[] arr, int[] arr_temp, int left, int right) { // 递归终止条件,子数组长度为1 if (left >= right) { return; } int mid = (left + right) / 2; sort(arr, arr_temp, left, mid); sort(arr, arr_temp, mid + 1, right); merge(arr, arr_temp, left, mid, right); } public static void merge(int[] arr, int[] arr_temp, int left, int mid, int right) { System.arraycopy(arr, left, arr_temp, left, right - left + 1); int i = left; int j = mid + 1; // 将需要合并的两个数组合起来全部遍历一遍,将其放入临时数组 for (int k = left; k <= right; k++) { // 先考虑两个边界问题,左边指针和右边指针都到头了,即一边处理结束的情况 // 左半边元素全部处理完毕,右半边元素都大于左半边,右边元素直接落下来到临时数组,右边指针动 if (i > mid) { arr[k] = arr_temp[j]; j ++; }else if (j > right) { // 右半边指针到头了,左半边元素都大于右半边,左边元素直接落下来到临时数组,左边指针动 arr[k] = arr_temp[i]; i ++; }else if (arr_temp[i] < arr_temp[j]) { // 比较,遍历到的左边元素小于右边元素,左边元素进入临时数组,左边指针右动一位 arr[k] = arr_temp[i]; i ++; }else { // 比较,遍历到的左边元素大于右边元素,右边元素进入临时数组,右边指针向右动一位 arr[k] = arr_temp[j]; j ++; } } } public static void main(String[] args) { //int[] arr = {5, 7, 8, 3, 1, 2, 4, 6, 8}; int[] arr = {3, 1, 2, 4}; //int[] arr = {1, 2, 3}; arr = mergeSort(arr); for (int i=0; i<arr.length; i++) { System.out.println(arr[i]); } }
}
稳定性分析
归并排序稳不稳定关键要看merge()函数,也就是两个有序子数组合并成一个有序数组的那部分代码。在合并的过程中,如果有相同的元素,可以按照顺序依次放入原数组中,这样就保证了值相同的元素,在合并前后的先后顺序不变。所以,归并排序是一个稳定的排序算法。
时间复杂度分析
归并排序涉及递归,时间复杂度的分析稍微有点复杂。我们正好借此机会来学习一下,如何分析递归代码的时间复杂度。
递归的适用场景是,一个问题a可以分解为多个子问题b、c,那求解问题a就可以分解为求解问题b、c。问题b、c解决之后,我们再把b、c的结果合并成a的结果。
如果我们定义求解问题a的时间是T(a),求解问题b、c的时间分别是T(b)和 T( c),那我们就可以得到这样的递推关系式: T(a) = T(b) + T(c) + K,其中K等于将两个子问题b、c的结果合并成问题 a 的结果所消耗的时间。
套用这个公式,我们来分析一下归并排序的时间复杂度。我们假设对n个元素进行归并排序需要的时间是T(n),那分解成两个子数组排序的时间都是T(n/2)。我们知道,merge()函数合并两个有序子数组的时间复杂度是O(n)。所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。
T(n) = 2*T(n/2) + n; n>1
通过这个公式,如何来求解T(n)呢?还不够直观?那我们再进一步分解一下计算过程。
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n
= 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n
= 8*T(n/8) + 3*n= 8*(2*T(n/16) + n/8) + 3*n
= 16*T(n/16) + 4*n ......
= 2^k * T(n/2^k) + k * n
通过这样一步一步分解推导,我们可以得到T(n) = 2^kT(n/2^k)+kn。
当T(n/2^k)=T(1)时,也就是n/2^k=1,我们得到 k=log2n 。
我们将k值代入上面的公式,得到T(n)=Cn+nlog2n 。如果我们用大O标记法来表示的话,T(n)就等于O(nlogn)。所以归并排序的时间复杂度是O(nlogn)。
从我们的原理分析可知,归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情 况,还是平均情况,时间复杂度都是O(nlogn)。
空间复杂度分析
归并排序的时间复杂度任何情况下都是O(nlogn),看起来非常优秀,因为上一篇分析到的即便是快速排序,最坏情况下,时间复杂度也是O(n2)。
注:快速排序算法虽然最坏情况下的时间复杂度是O(n2),但是平均情况下时间复杂度都是O(nlogn)。不仅如此,快速排序算法时间复杂度退化到O(n2)的概率非常小, 我们可以通过合理地选择pivot来避免这种情况。。
但是,归并排序并没有像快排那样,应用广泛,因为它有一个致命的“弱点”,那就是归并排序不是原地排序算法。
通过代码和上面的讲解也知道我借助了和原数组大小相同的数组来进行辅助排序,所以空间复杂度是O(n)。
归并排序和快速排序对比
相同点:
- 都采用分治算法
- 都可以递归实现
- 平均时间复杂度都是O(nlogn)
不同点:
- 归并排序是先切分、后排序,快速排序是切分、排序交替进行;
- 归并排序是稳定的排序,而快速排序是不稳定的排序;
- 归并排序在最坏和最好情况下的时间复杂度均为O(nlogn),而快速排序最坏O(n^2),最好O(n);
- 快速排序是原地排序,归并不是。
OC代码
- (void)megerSortAscendingOrderSort:(NSMutableArray *)ascendingArr { //tempArray数组里存放ascendingArr个数组,每个数组包含一个元素 NSMutableArray *tempArray = [NSMutableArray arrayWithCapacity:1]; for (NSNumber *num in ascendingArr) { NSMutableArray *subArray = [NSMutableArray array]; [subArray addObject:num]; [tempArray addObject:subArray]; } //开始合并为一个数组 while (tempArray.count != 1) { NSInteger i = 0; while (i < tempArray.count - 1) { tempArray[i] = [self mergeArrayFirstList:tempArray[i] secondList:tempArray[i + 1]]; [tempArray removeObjectAtIndex:i + 1]; i++; } } NSLog(@"归并升序排序结果:%@", tempArray[0]); } - (NSArray *)mergeArrayFirstList:(NSArray *)array1 secondList:(NSArray *)array2 { NSMutableArray *resultArray = [NSMutableArray array]; NSInteger firstIndex = 0, secondIndex = 0; while (firstIndex < array1.count && secondIndex < array2.count) { if ([array1[firstIndex] floatValue] < [array2[secondIndex] floatValue]) { [resultArray addObject:array1[firstIndex]]; firstIndex++; } else { [resultArray addObject:array2[secondIndex]]; secondIndex++; } } while (firstIndex < array1.count) { [resultArray addObject:array1[firstIndex]]; firstIndex++; } while (secondIndex < array2.count) { [resultArray addObject:array2[secondIndex]]; secondIndex++; } return resultArray.copy; }
注意





