22*:排序算法5:堆排序(完全二叉树大堆顶,交互堆顶和最后元素,找到最大元素。递归依次排序。)
问题
目录
预备
正文
一:什么是堆?
1:定义
堆(英语:Heap)是计算机科学中的一种特别的完全二叉树,满足特性"给定堆中任意节点P和C,若P是C的母节点,那么P的值会小于等于(或大于等于)C的值"。 摘自维基百科。
首先堆是一个完全二叉树(除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列),这点很重要,直接决定了数组下标和左右父节点的对应关系(关系往下看)。
2:分类
最大堆(max heap):母节点的值恒大于等于子节点的值;
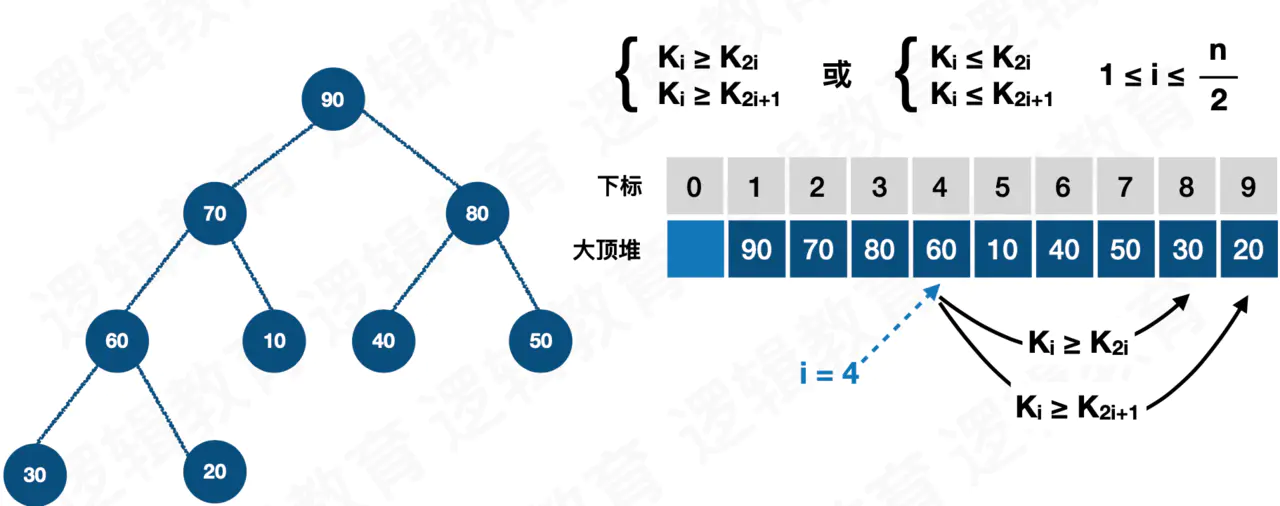
最小堆(min heap):母节点的值恒小于等于子节点的值;
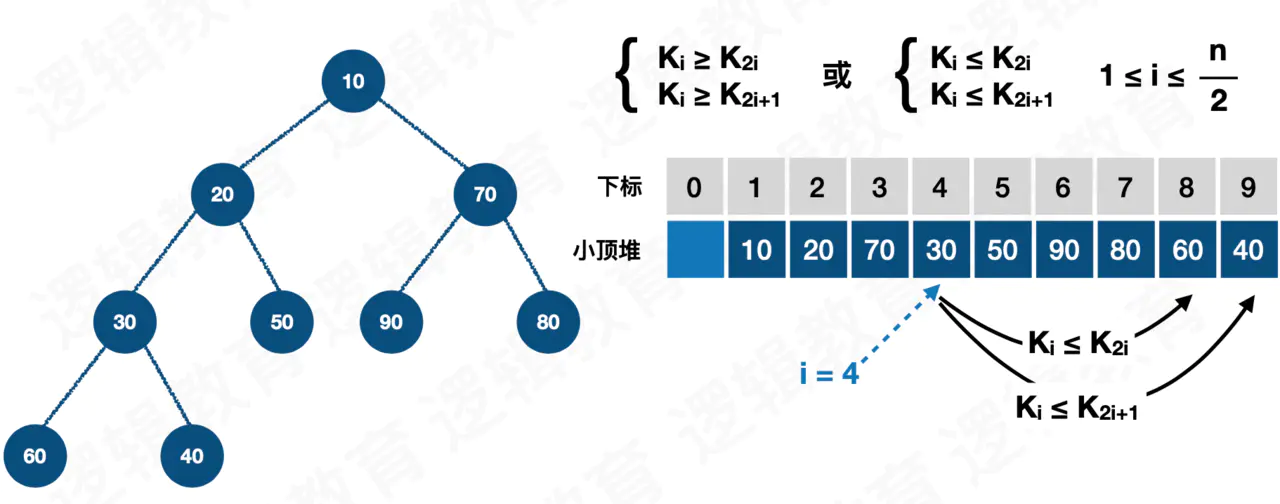
值得注意,这个地方对左右子节点的大小没有要求。
而且,堆一般用数组来存储,而不是树。因为树需要为其左右子节点分配指针空间,而数组使用数组下标来表示左右子节点的位置,可以说堆是被树耽误了的数组,顶着树的光环,实际上干着数组该干的事儿,
父节点和左右子节点在数组中的位置关系:
parent(i) = arr((i - 1)/2) left(i) = 2i + 1 right(i) = 2i + 2
二:堆排序
正因为堆只是父子之间大小关系确定,左右子节点直接大小不确定,所以才要堆排序将所有的元素有序排序。
1:算法描述
以构建大顶堆为例:
- 将待排序序列构成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点;
- 将其与末尾元素进行交换,此时末尾就是最大值;
- 然后将剩余n-1个元素重新构造成一个大顶堆,就会得到n个元素的次大值;
- 反复执行前面2,3步,便能得到一个有序序列
2:动图演示

3:图解堆排序
根据数组构造大顶堆:
- 初始数组为:[6,1,2,3,0,4,5,7]
- 按照完全二叉树,将数字依次填入,得到图中第一幅图;
- 从最下面的非叶子结点开始(非叶子结点为 arr.length/2-1 = 8/2-1 =3,父节点是arr[0],arr[3]也就是3)调整,根据性质,左右子节点中小的数字往上移动;
- 从下至上,从右往左,递归,直到根节点
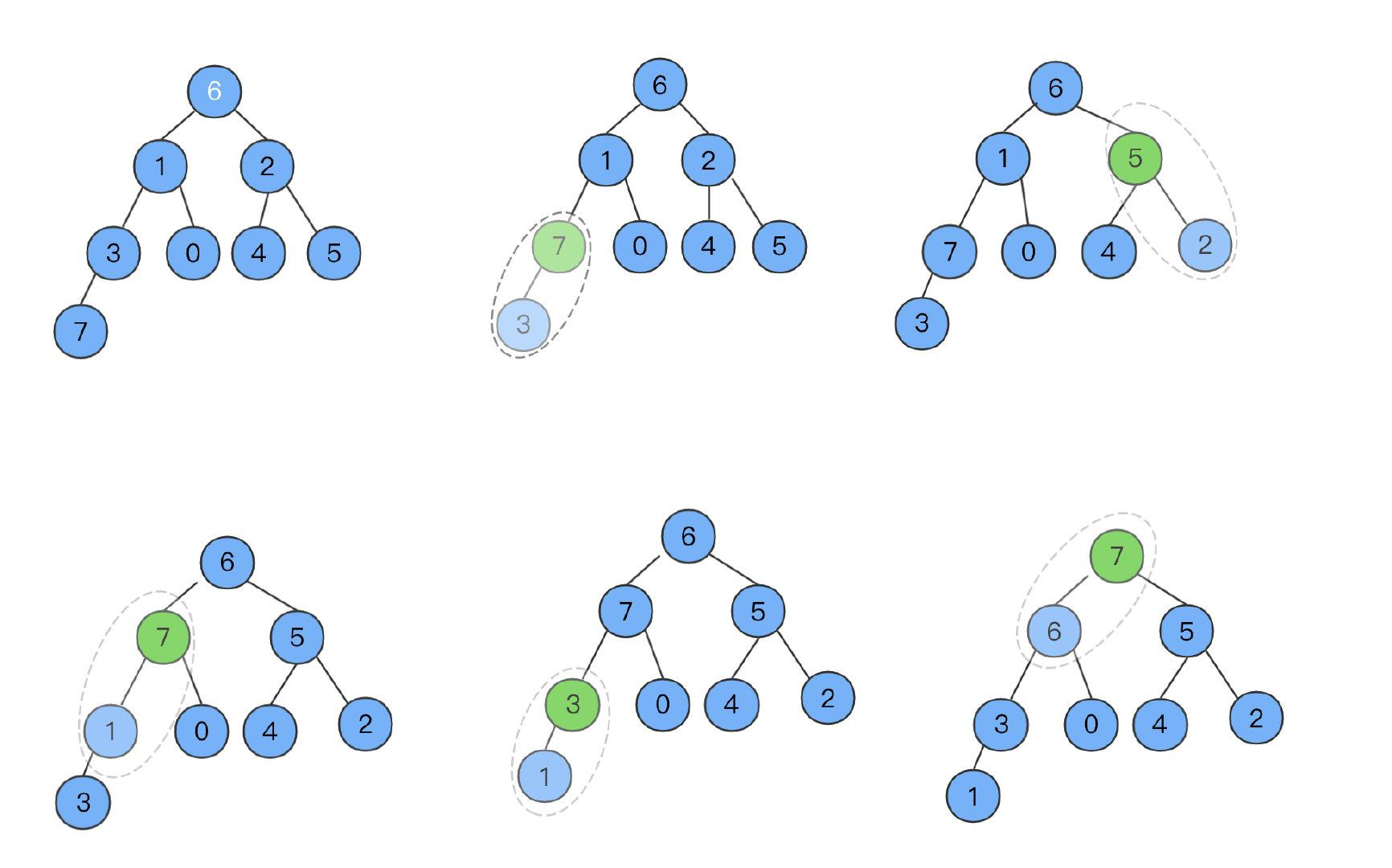
一次调整之后7成功上位,得到数组最大的值7,与此同时数组对应的大顶堆构造完成。
由下至上的堆有序化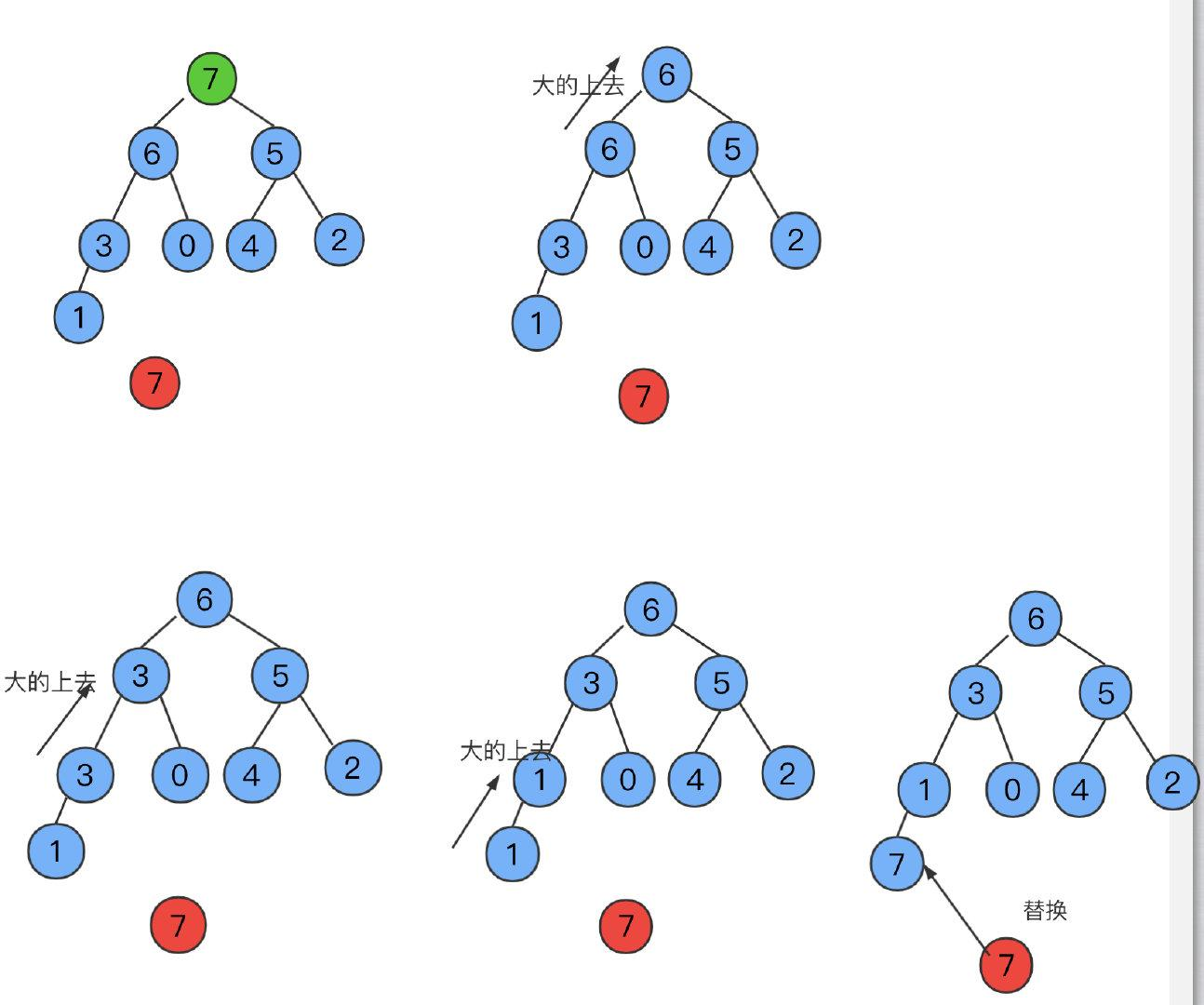
这里可以看到,交换调整之后最大的元素到了最下面,最终会是越下面的数越大,因此构造大顶堆得到的是降序,升序要构造小顶堆。
import com.sun.tools.javac.util.ArrayUtils; /** * @author by zengzhiqin * 2020-12-10 */ public class HeapSort { public static int[] heapSort (int[] arr) { if (arr == null && arr.length == 0) { throw new RuntimeException("数组不合法"); } // 构建大堆(从最下面叶子结点层的上一层,即倒数第二层的第一个开始进行构建调整) for (int i = arr.length / 2 -1; i >= 0; i--) { adjustDown(arr, i, arr.length); } // 循环调整下沉 for (int i = arr.length -1; i >= 0; i--) { swap(arr, 0, i); adjustDown(arr, 0, i); } return arr; } /** * 调整 * @param arr * @param parent * @param length */ public static void adjustDown (int[] arr, int parent, int length) { // 临时元素保存要下沉的元素 int temp = arr[parent]; // 左节点的位置 int leftChild = 2 * parent + 1; // 开始往下调整 while (leftChild < length) { // 如果右孩子节点比左孩子大,则定位到右孩子 (父节点只是比左右孩子都大,左右孩子大小不确定) if(leftChild + 1 < length && arr[leftChild] < arr[leftChild + 1]) { // 此时leftChild实际上是右孩子,但始终是左右里面最大的 leftChild ++ ; } // 大顶堆条件被破坏了 if (arr[leftChild] <= temp) { break; } // 把子节点中大的值赋值给父节点 arr[parent] = arr[leftChild]; // 大的子节点为父节点,调整它的左右子节点 parent = leftChild; leftChild = 2 * parent + 1; } arr[parent] = temp; } /** * 交换数组中两个元素 * @param arr 数组 * @param i 父元素 * @param index 元素2 */ public static void swap (int[] arr, int i, int index) { int temp = arr[i]; arr[i] = arr[index]; arr[index] = temp; } public static void main(String[] args) { //int[] arr = {5, 7, 8, 3, 1, 2, 4, 6, 8}; int[] arr = {3, 1, 2, 4}; //int[] arr = {1, 2, 3}; arr = heapSort(arr); for (int i=0; i<arr.length; i++) { System.out.println(arr[i]); } } }
稳定性分析
不稳定。
时间复杂度分析
nlog(n)。
大顶堆构造使用 O(N) 的时间,元素调整下滤需要 O(logN),需要下滤 N-1 次,所以总共需要 O(N+(N-1)logN) = O(NlogN)。从过程可以看出,堆排序,不管最好,最坏时间复杂度都稳定在O(NlogN)。
空间复杂度分析
原地排序,空间复杂度O(1)
//大顶堆调整函数; /* 条件: 在L.r[s...m] 记录中除了下标s对应的关键字L.r[s]不符合大顶堆定义,其他均满足; 结果: 调整L.r[s]的关键字,使得L->r[s...m]这个范围内符合大顶堆定义. */ void HeapAjust(SqList *L,int s,int m){ int temp,j; //① 将L->r[s] 存储到temp ,方便后面的交换过程; temp = L->r[s]; //② j 为什么从2*s 开始进行循环,以及它的递增条件为什么是j*2 //因为这是颗完全二叉树,而s也是非叶子根结点. 所以它的左孩子一定是2*s,而右孩子则是2s+1;(二叉树性质5) for (j = 2 * s; j <=m; j*=2) { //③ 判断j是否是最后一个结点, 并且找到左右孩子中最大的结点; //如果左孩子小于右孩子,那么j++; 否则不自增1. 因为它本身就比右孩子大; if(j < m && L->r[j] < L->r[j+1]) ++j; //④ 比较当前的temp 是不是比较左右孩子大; 如果大则表示我们已经构建成大顶堆了; /* 将无序的树构建成大顶堆时候先将下面的构建成,变量往上构建 */ if(temp >= L->r[j]) break; //⑤ 将L->[j] 的值赋值给j和j+1两个叶子节点的根结点 L->r[s] = L->r[j]; //⑥ 将s指向j; 因为此时L.r[4] = 60, L.r[8]=60. 那我们需要记录这8的索引信息.等退出循环时,能够把temp值30 覆盖到L.r[8] = 30. 这样才实现了30与60的交换; //然后再对比较大的叶子的子树进行处理,让它成为大顶堆 s = j; } //⑦ 将L->r[s] = temp. 其实就是把L.r[8] = L.r[4] 进行交换; L->r[s] = temp; } //10.堆排序--对顺序表进行堆排序 void HeapSort(SqList *L){ int i; //1.将现在待排序的序列构建成一个大顶堆; //将L构建成一个大顶堆; //i为什么是从length/2.因为在对大顶堆的调整其实是从第一个非叶子的根结点开始进行调整,然后遍历往上排序 for(i=L->length/2; i>0;i--){ HeapAjust(L, i, L->length); } //2.逐步将每个最大的值根结点与末尾元素进行交换,并且再调整成大顶堆 for(i = L->length; i > 1; i--){ //① 将堆顶记录与当前未经排序子序列的最后一个记录进行交换; swap(L, 1, i); //② 将L->r[1...i-1]重新调整成大顶堆; /* 因为从顶部开始调整的时候,只是原本树已经是大堆顶了,只是将根结点和最后一个元素进行了交换而已,所以再调整只是将最顶端的值调整到合适位置,这样就减少了遍历 */ HeapAjust(L, 1, i-1); } }
OC代码
- (void)heapSort:(NSMutableArray *)list { NSInteger i ,size; size = list.count; //找出最大的元素放到堆顶 for (i= list.count/2; i>=0; i--) { [self createBiggesHeap:list withSize:size beIndex:i]; } while(size > 0){ [list exchangeObjectAtIndex:size-1 withObjectAtIndex:0]; //将根(最大) 与数组最末交换 size -- ;//树大小减小 [self createBiggesHeap:list withSize:size beIndex:0]; } NSLog(@"%@",list); } - (void)createBiggesHeap:(NSMutableArray *)list withSize:(NSInteger) size beIndex:(NSInteger)element { NSInteger lchild = element *2 + 1,rchild = lchild+1; //左右子树 while (rchild < size) { //子树均在范围内 if (list[element]>=list[lchild] && list[element]>=list[rchild]) return; //如果比左右子树都大,完成整理 if (list[lchild] > list[rchild]) { //如果左边最大 [list exchangeObjectAtIndex:element withObjectAtIndex:lchild]; //把左面的提到上面 element = lchild; //循环时整理子树 }else{//否则右面最大 [list exchangeObjectAtIndex:element withObjectAtIndex:rchild]; element = rchild; } lchild = element * 2 +1; rchild = lchild + 1; //重新计算子树位置 } //只有左子树且子树大于自己 if (lchild < size && list[lchild] > list[element]) { [list exchangeObjectAtIndex:lchild withObjectAtIndex:element]; } }
堆排序运行时间主要是消耗在初始构建堆和在重建堆时的反复筛选上。在构建堆的过程中,对每个终端节点最多进行两次比较操作,因此整个排序堆的时间复杂度为O(n)。
空间复杂度上,它只有一个用来交换的暂存单元,也是非常不错。不过由于记录的比较和交换是跳跃式进行,因此堆排序也是一种不稳定的排序方法。
另外,由于初始构建堆排序需要的比较次数较多,因此,它不适合待排序序列个数较少的情况。
注意



