21*:排序算法4:希尔排序(缩小增量排序)
问题
//起始间隔值gap设置为总数的一半,直到gap==1结束 -(void)shellSort:(NSMutableArray *)list{ int gap = (int)list.count / 2; while (gap >= 1) { for(int i = gap ; i < [list count]; i++){ NSInteger temp = [[list objectAtIndex:i] intValue]; int j = i; while (j >= gap && temp < [[list objectAtIndex:(j - gap)] intValue]) { [list replaceObjectAtIndex:j withObject:[list objectAtIndex:j-gap]]; j -= gap; } [list replaceObjectAtIndex:j withObject:[NSNumber numberWithInteger:temp]]; } gap = gap / 2; } }
目录
预备
冒泡,选择和插入排序,它们的时间复杂度都是O(n*2),比较高,适合小规模数据的排序,当有大规模的数据需要排序的时候这三种排序算法就有点吃不消了,所以需要进行优化,先来看看优化的思路:
-
首先,冒泡,选择和插入排序的第一步都是全部遍历,要想再有突破,将平均时间复杂度降低到O(n log n),那肯定不能从头遍历了,考虑一下部分遍历。
-
其次冒泡排序和插入排序的时间复杂度,在最好情况和最坏情况下差了一个指数级别,这个地方有很大的优化空间让大神们发挥。
实际上,欲抱琵琶半遮面的希尔排序和大概是个程序员都听说过但大部分人都不清楚的快速排序,分别就是插入排序和冒泡排序的变种,而且这两个排序分别前后脚,一个在1959年另一个于1960年问世。
正文
希尔排序O(n longn)
1:算法描述
优化依据:插入排序在最好情况下,数据都是有序时,遍历一次数据即可时间复杂度为O(n);最坏情况下刚好数据倒序时为(n^2-n)/2即时间复杂度O(n^2),可知插入排序算法时间复杂度到底是 n 还是 n^2 和原始数据是否有序息息相关,原始数据有序的话,插入时比较次数越少,挪动的位置也越少(例子:如果倒序,最后一个数据要一个一个和前面的比较大小,挪动N-1次,才可以到最前面)。
希尔优化思路:所以,希尔就是从这个点着手优化的,先将整个数组进行宏观调控,使用分组的方式,分组策略使用一个递减序列,每组依然使用插入排序算法进行组内排序,最后将分组都组合起来,这样局部宏观调控之后每组都有序即局部有序,局部调控的效果是可喜的(看看下图一个完全倒序数组第一遍宏观调控的效果);一直分组下去,直到分组为1,组内就是全部元素了,分组越少,组内成员就越多,局部有序元素就越多,当分组为1的时候,全部元素都是一组,而且这组已经被宏观调控的大致有序,最后这组仍然使用插入排序算法进行微调,即全部有序,全排序。
10长度完全倒序数组,按照从小到大排序,分10/2=5组:
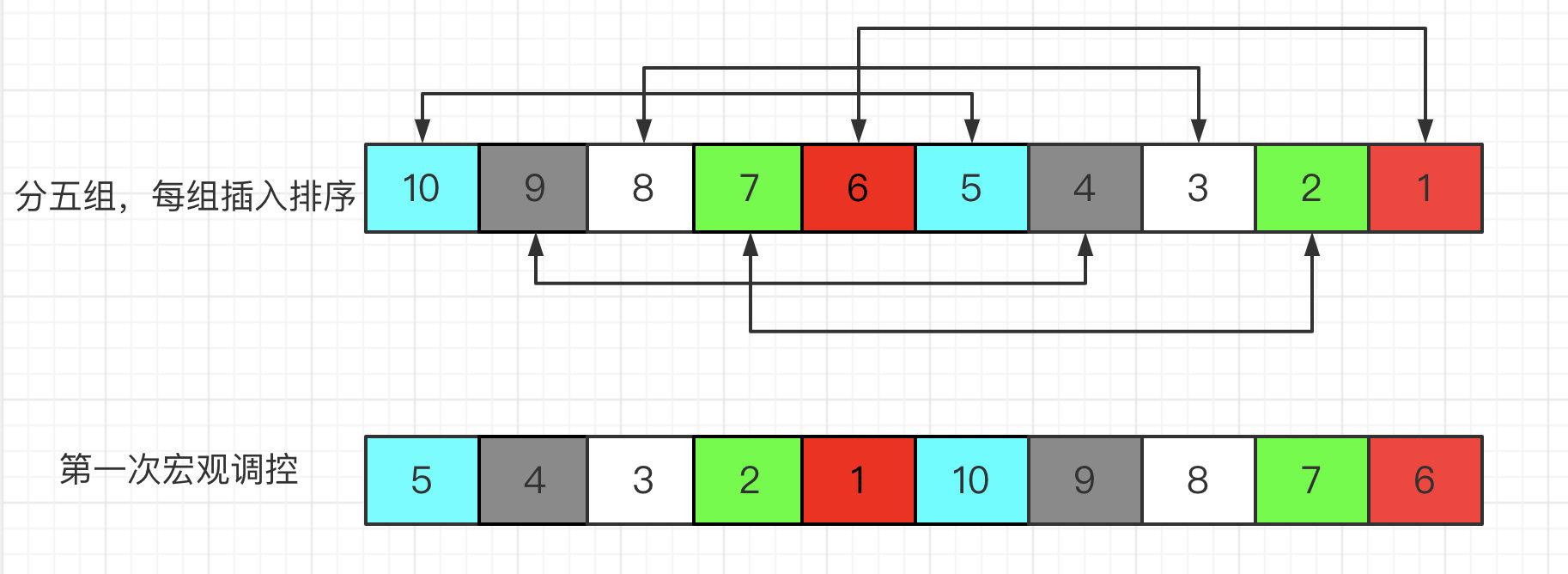
每组都有序了,大的元素几乎都被调到后面去了。再往后细分组5/2=2,2/2=1组,最后全排序了。
2:算法思想
-
将数组分为 h 组,初始 h 一般定为 n 的1/2或者1/3,交换间隔为 h 的元素进行局部排序,数据顺序不对可以直接跳过 h 个位置一步“交换”到前面去,
每次使得任意间隔为 h 的元素都是有序的,nice哇。然后每次遍历 h/2, 直到 h=1, 组越分越小,当 h=1 的时候,整个数组已经被调整到非常有序了,再使用我们的插入排序算法进行微调,bingo,全排序!抛出概念帮助理解和总结,希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(h就是增量,一直变小),上面提到的数组称为 h 有序数组,一个 h 有序数组就是 h 个互相独立的有序数组编织在一起组成的一个完整数组。
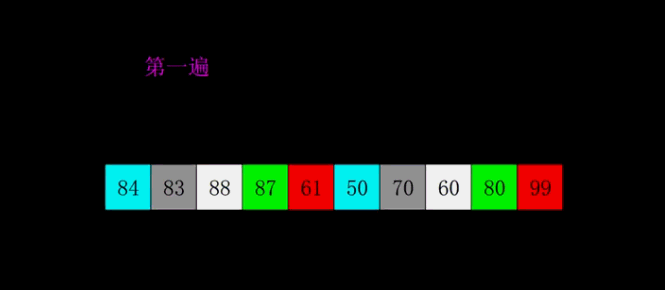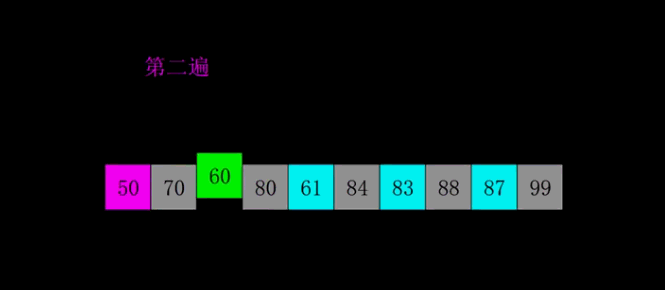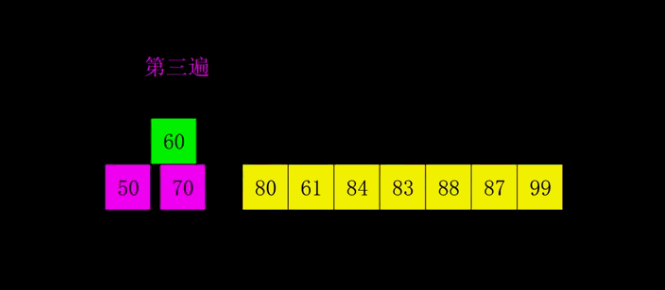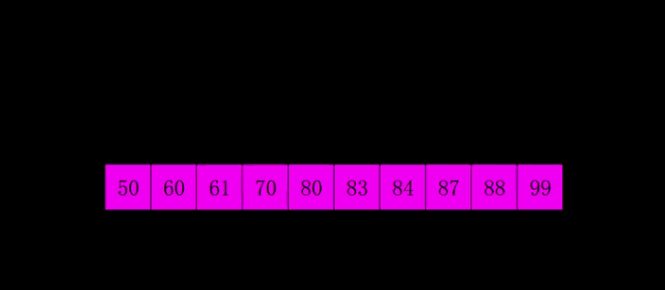
-
颜色相同的代表同一组
-
前两遍都是宏观调控局部排序,只有数据交换没有挪位操作
-
最后一遍是插入排序,微调
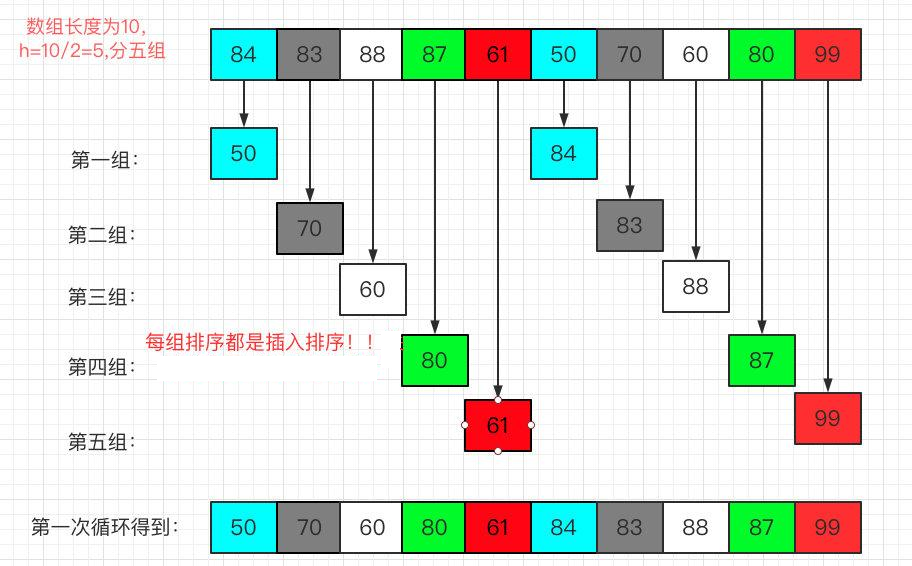
3.1:第一遍
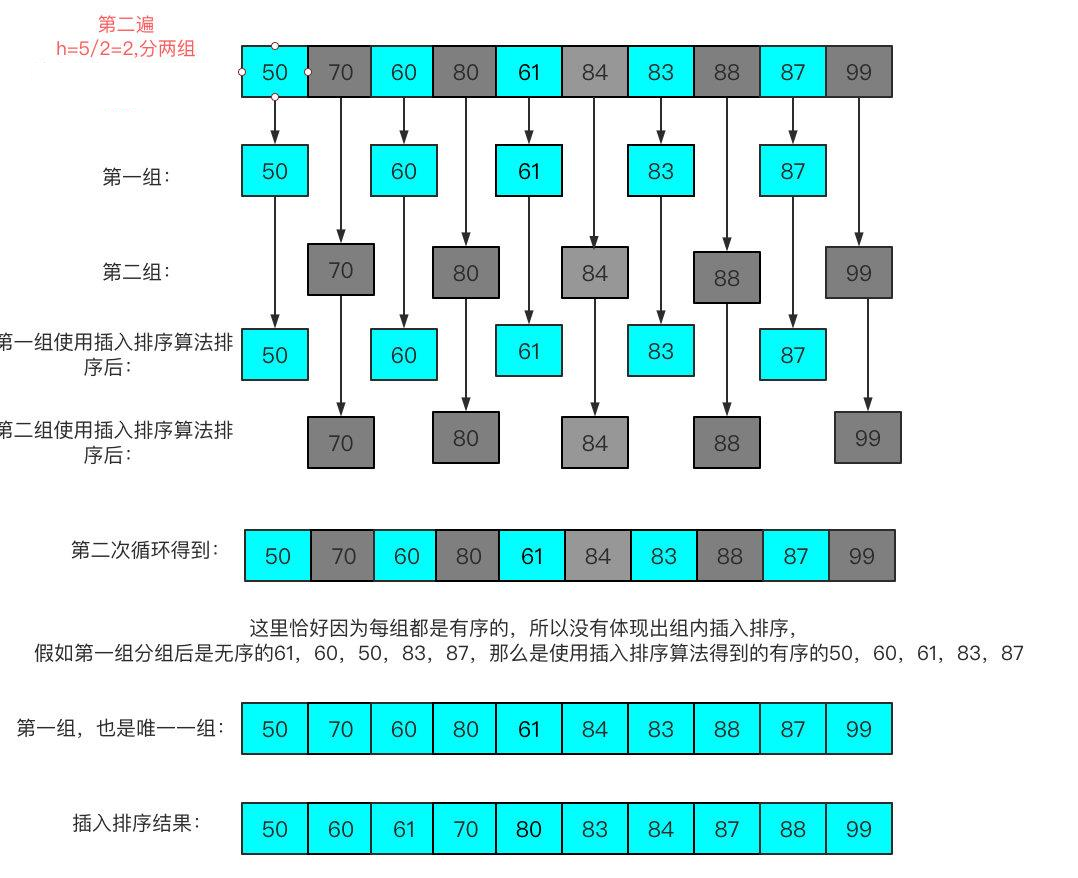
3.2:第二遍
为什么第一遍,第二遍不需要挪位?
第一遍每组只有2个元素,是在本组使用插入排序,直接插入到前面就可了,不用挪位,但是还是插入排序算法。
第二遍是因为我这组数据,在第二遍每组都是有序的,也不需要挪位插入,但是动画可看出是比较了的。
第三遍可以很直观的看出来是插入排序算法了。
public class ShellSort { public static int[] shellSort(int arr[]) { if (arr == null || arr.length < 2) { return arr; } int n = arr.length; // 对每组间隔为 h 的元素进行排序,刚开始 h = n / 2; for (int h = n / 2; h > 0; h /= 2) { // i代表第几组,对各个局部分组轮流进行插入排序 for (int i = h; i < n; i++) { // 轮流对每个分组进行插入排序 insertSort(arr, h, i); } } return arr; } /** * 局部插入排序 * @param arr 原数组 * @param h 分组内元素个数,分组数,间隔数,递增数; 例如栗子中第一次分组 f=5 是 {arr[0],arr[5]]} ,{arr[1],arr[6]]}, {arr[2],arr[7]]} ...... * @param f 每个分组的第二个元素,默认第一个元素有序,从第二个元素开始排 */ private static void insertSort(int[] arr, int h, int f) { int n = arr.length; // 下标为0的数默认是有序的,从下标为1的数开始遍历,将其放入他该去的地方 for (int i = f; i < n; i++) { // 申请一个变量记录要插入的数据,也就是动图中取出来的元素 int tmp = arr[i]; // 从已经排序的序列最右边的开始比较,找到比其小的数 int j = i; // 原本插入排序间隔 1 改为间隔 h,上一篇插入排序是 j>0,其实和 j>=1 等价,这里是 j>=h 不难理解 while (j >= h && tmp < arr[j - h]) { // 在局部数组中后挪一位 arr[j] = arr[j-h]; j -= h; } // 存在比其小的数,插入 if (j != i) { arr[j] = tmp; } } } }
-
看代码可知,插入排序几乎是一样的,只不过改成了分组插入排序的逻辑,1变成了h而已。
-
稳定性分析
不稳定。
首先我们知道插入排序是稳定的,因为插入排序每次插入一个数据都能保证他的顺序是相对有序,不必被相同大小元素打乱了顺序,他保证了排好序的那边分区的有序性。
但是希尔排序只能保证分组内的元素有序,相同大小元素,排在很后面的可能在一次分组排序中直接被调到了前面,因此排序就会乱。例如数组arr为 3 1 1 2,按照希尔排序,第一次分组 [arr[0], arr[2]],[arr[1],arr[3]] 即[3,1],[1,2],第三个 1 直接去了前面。
-
时间复杂度分析
最好和最坏情况下都一样
OC代码
//起始间隔值gap设置为总数的一半,直到gap==1结束 -(void)shellSort:(NSMutableArray *)list{ int gap = (int)list.count / 2; while (gap >= 1) { for(int i = gap ; i < [list count]; i++){ NSInteger temp = [[list objectAtIndex:i] intValue]; int j = i; while (j >= gap && temp < [[list objectAtIndex:(j - gap)] intValue]) { [list replaceObjectAtIndex:j withObject:[list objectAtIndex:j-gap]]; j -= gap; } [list replaceObjectAtIndex:j withObject:[NSNumber numberWithInteger:temp]]; } gap = gap / 2; } //或者 // while (gap >= 1) { // for(int i = gap ; i < [list count]; i++){ // int temp = [list[i] intValue]; // int j = i; // while (j >= gap && temp < [list[j - gap] intValue]) { // [list exchangeObjectAtIndex:j withObjectAtIndex:j-gap]; // j -= gap; // } // } // gap = gap / 2; // } }
希尔排序优势:希尔排序优化了插入排序,在性能上比选择排序和插入排序快得多,而这种优势会随着数组越大变得越为明显。而且算法代码短简单,非常容易实现,所以我们基本上所有排序工作一开始都是用希尔排序,若在实际中不够快,我们再改成快速排序等更为高级的算法。
希尔排序劣势: 希尔排序没有快速排序算法快 O(n(logn)),因此中等大小规模表现良好,对规模非常大的数据排序不是最优选择。
注意



