19*:排序算法2:选择排序(从未排序区间找最小元素,和排序区间的最后一个元素交换位置。)
问题
- (void)selectionAscendingOrderSortWithArray:(NSMutableArray *)ascendingArr { int index = 0;//记录找到的关键字下标 for (int i = 0; i < arr.count - 1; i++) { index = i; for (int j = i + 1; j < arr.count; j++) { if ([arr[index] integerValue] < [arr[j]integerValue]) { //如果有比当前index值大的值,则记录次下标 index = j;//记录最大值(最小值)的下标 } } if (i != index) { //若index不等于i,说明找到最大值,交换 [arr exchangeObjectAtIndex:i withObjectAtIndex:index]; } NSLog(@"%@",arr); }
目录
预备
正文
1:选择排序
1:算法描述
给定 N个项目和 L = 0的数组,选择排序将:
- 在 [L ... N-1]范围内找出最小项目 X的位置,
- 用第 L项交换X,
- 将下限 L增加1并重复步骤1直到 L = N-2。
2:算法思想
选择排序分已排序区间和未排序区间,其实就是从头遍历,要排第几个元素,每次从剩余未排序元素里面找最小的元素,交换位置。
重复(元素个数-1)次 把第一个没有排序过的元素设置为最小值 遍历每个没有排序过的元素 如果元素 < 现在的最小值 将此元素设置成为新的最小值 将最小值和第一个没有排序过的位置交换
3:动图演示
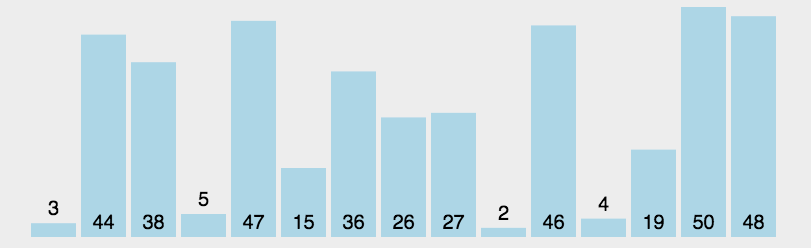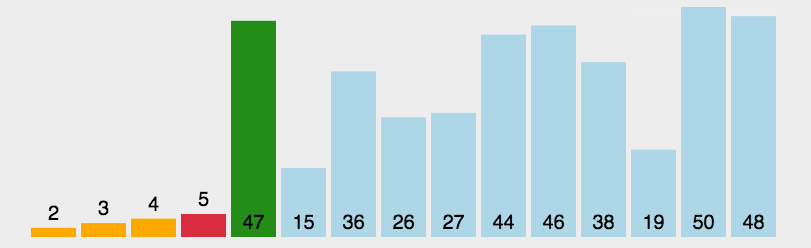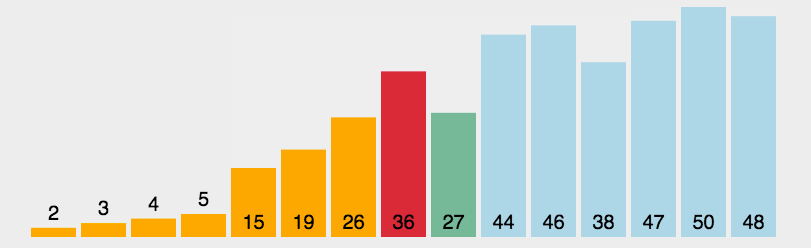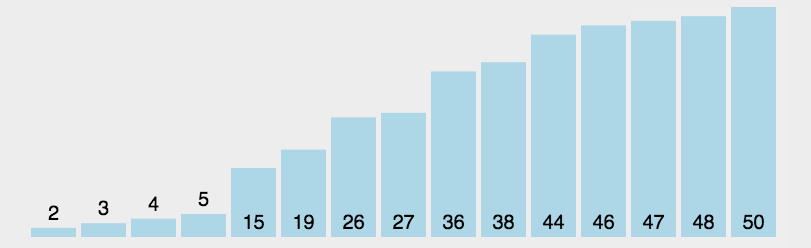
- 红色表示当前遍历到的最小值
-
黄色的条代表已经排好序的元素;
-
绿色的代表此算法正在操作,进行比较交换的元素
-
蓝色代表还没有排序的
4:代码实现
public class SelectSort { public static int[] selectSort(int[] a) { int n = a.length; // 从头开始遍历,选定某个元素待排序 for (int i = 0; i < n - 1; i++) { // 将这个元素设为最小值 int min = i; // 遍历所有未排过序的元素,从第i个元素右边开始 for (int j = i + 1; j < n; j++) { // 如果元素小于当前最小值,那么最小值改为当前值 if(a[min] > a[j]) min = j; } // 以上得到了当前最小值,将当前最小值提到前面 //交换 int temp = a[i]; a[i] = a[j]; a[j] = temp; } return a; } }
-
稳定性分析
不稳定。从动画当中可以看出,选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素交换位置,这样破坏了稳定性。
如果你还是难以理解,那么举个栗子,比如4,6,4,2,7这样一组数据,使用选择排序算法来排序的话,第一次找到最小元素2,与第一个5交换位置,那第一个4和中间的4顺序就变了,所以就不稳定 了。正是因此,相对于冒泡排序和插入排序,选择排序就稍微逊色了。
-
时间复杂度分析
最好和最坏情况都是n的平方,因为每次都是去查寻最小的元素,第二层的遍历无论如何也要做,避免不了,因此选择排序可谓是弟中弟。
OC代码
原理:从第一个元素开始,依次查找对比,找到最小的元素与第一个元素交换,再从第二个元素开始找后面元素的最小值与第二个元素交换,以此类推,直到整个数组有序。
时间复杂度和空间复杂度与冒泡排序一样
- (void)selectionAscendingOrderSortWithArray:(NSMutableArray *)ascendingArr { int index = 0;//记录找到的关键字下标 for (int i = 0; i < arr.count - 1; i++) { index = i; for (int j = i + 1; j < arr.count; j++) { if ([arr[index] integerValue] < [arr[j]integerValue]) { //如果有比当前index值大的值,则记录次下标 index = j;//记录最大值(最小值)的下标 } } if (i != index) { //若index不等于i,说明找到最大值,交换 [arr exchangeObjectAtIndex:i withObjectAtIndex:index]; } NSLog(@"%@",arr); }
冒泡与选择对比:
选择比冒泡效率高,一次循环只交换一次,冒泡也可以记录坐标进行一次交换,但空间复杂度就增加,冒泡可以检验数组是否有序,如果循环中没有一次交换说明是有序的,可以提前终止
冒泡排序在内循环交换,选择排序在外循环交换,效率差也就在这个交换次数上,毕竟O(n)<O(n^2)。如果数组完全有序,冒泡内循环的交换一次都不会执行,而选择排序每次还要和本身交换一次,此时冒泡效率高。
注意



