18*:排序算法1:冒泡和优化(未排序区间两两交换找到最大值,排在最后,形成有序区间。稳定)
问题
-(void)bubbleSequence:(NSMutableArray *)arr {//优化后算法-从第一个开始排序,空间复杂度相对更大一点 for (int i = 0; i < arr.count; ++i) { bool flag=false; //遍历数组的每一个`索引`(不包括最后一个,因为比较的是j+1) for (int j = 0; j < arr.count-1-i; ++j) { //根据索引的`相邻两位`进行`比较` if ([arr[j+1] intValue] < [arr[j] intValue]) { flag = true; [arr exchangeObjectAtIndex:j withObjectAtIndex:j+1]; } } if (!flag) { break;//没发生交换直接退出,说明是有序数组 } } }
目录
预备
正文
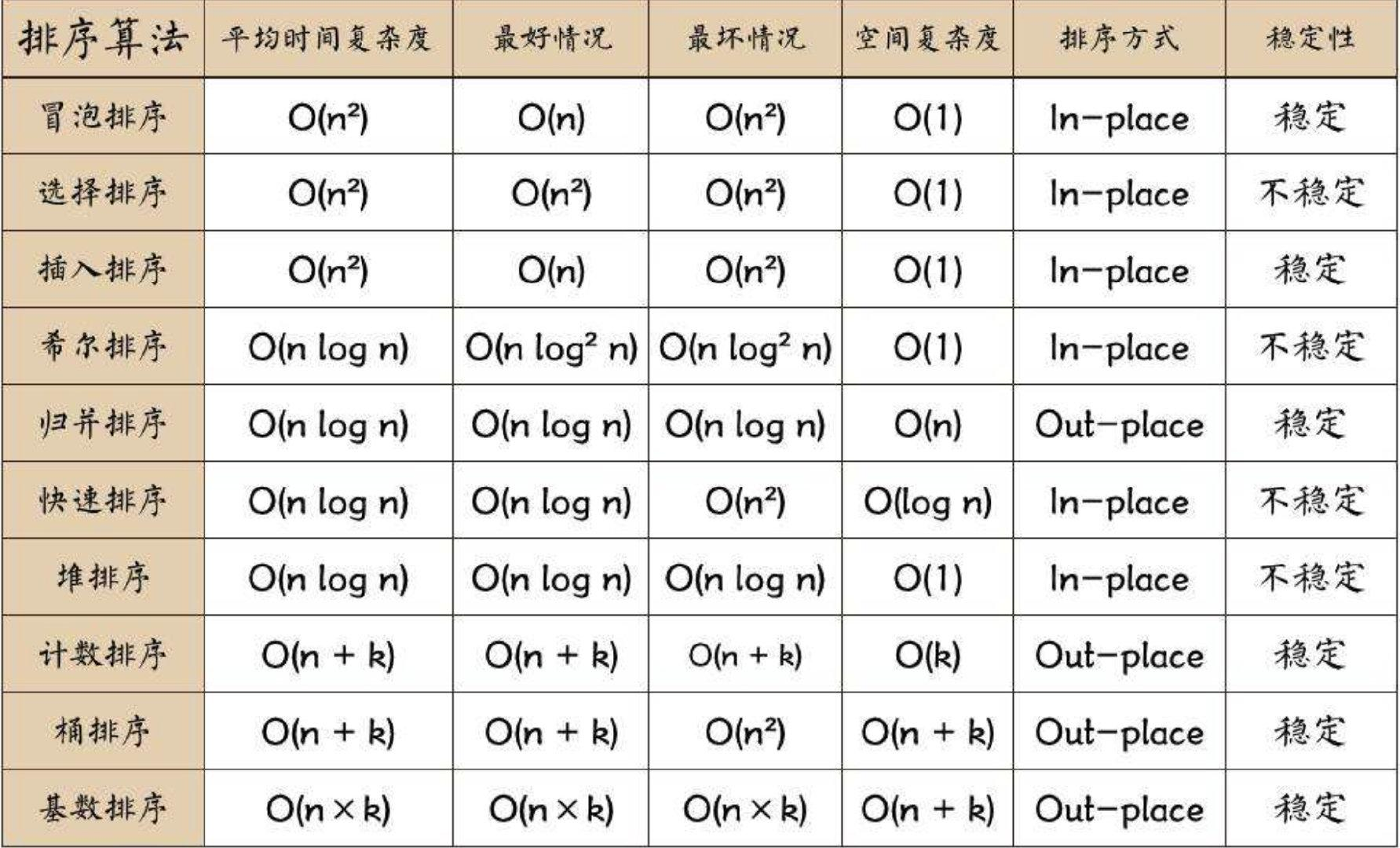
一:排序算法衡量指标
1:排序算法的衡量指标:
-
时间复杂度
-
空间复杂度
-
最好情况
-
最坏情况
-
比较次数,交换次数
-
稳定性
-
稳定性解释:比如我们有一组数据2,9,3,4,8,3,按照大小排序之后就是2,3,3,4,8,9。 这组数据里有两个3。经过某种排序算法排序之后,如果两个3的前后顺序没有改变,那我们就把这种排序算法叫作稳定的排序算法;如果前后顺序发生变化,那对应的排序算法就叫作不稳定的排序算法。
-
为什么要关注稳定性?
脱离了实际运用的数据结构是没有意义的,真正软件开发中,我们要排序的往往不是单纯的整数,而是一组对象,我们需要按照对象 的某个key来排序。
比如说,我们现在要给电商交易系统中的“订单”排序。订单有两个属性,一个是下单时间,另一个是订单金额。如果我们现在有10万条订单数据,我们希望按照金额从小到大对订单数据排序。对于金额相同的订单,我们希望按照下单时间从早到晚有序。对于这样一个排序需求,我们怎么来做呢?
-
直接思路:我们先按照金额对订单数据进行排序,然后,再遍历排序之后的订单数据,对于每个金额相同的小区间再按照下单时间排序。这种排序思路理解起来不难,但是实现起来会很复杂。
-
稳定排序算法思路:这个问题可以非常简洁地解决,我们先按照下单时间给订单排序,注意是按照下单时间,不是金额。排序完成之后,我们用稳定排序算法,按照订单金额重新排序。两遍排序之后,我们得到的订单数据就是按照金额从小到大排序,金额相同的订单按照下单时间从早到晚排序的。
-
为什么呢?稳定排序算法可以保持金额相同的两个对象,在排序之后的前后顺序不变。第一次排序之后,所有的订单按照下单时间从早到晚有序了。在第二次排序中,我们用的是稳定的排序算法,所以经过第二次排序之后,相同金额的订单仍然保持下单时间从早到晚有序。
-
-
是否原地(原址,就地)排序
维基百科说的原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。简单理解为,允许借助几个变量,不需要额外开数组。
属于原地排序的是:希尔排序、冒泡排序、插入排序、选择排序、堆排序、快速排序,他们都会有一项比较且交换操作(swap(i,j))的逻辑在其中;而合并排序,计数排序,基数排序等不是原地排序。

排序方式In-Place指的是原地排序,Out-place指的非原地排序
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(logn)<Ο(n)<Ο(nlogn)<Ο(n*2)<Ο(n*3)<Ο(n!)
二:冒泡排序
这个排序不简单,大学里面每个学校都必教的一个排序
1:算法描述
给定一个N个元素的数组,冒泡法排序将:
- 比较一对相邻元素(a,b);
- 如果元素大小关系不正确,交换这两个数;
- 重复步骤1和2,直到我们到达数组的末尾(最后一对是第(N-2)和(N-1)项,因为我们的数组从零开始)
- 第一次循环比较结束,最大的元素将在最后的位置。 然后我们将N减少1,并重复步骤1,直到N = 1。
2:算法思想
一次冒泡会让至少一个元素移动到它应该在的位置,重复n次,就完成了n个数据的排序工作。
交换旗帜变量 = 假 (False) 从 i = 1 到 最后一个没有排序过元素的指数 如果 左边元素 > 右边元素 交换(左边元素,右边元素) 交换旗帜变量 = 真(True)
3:动图演示
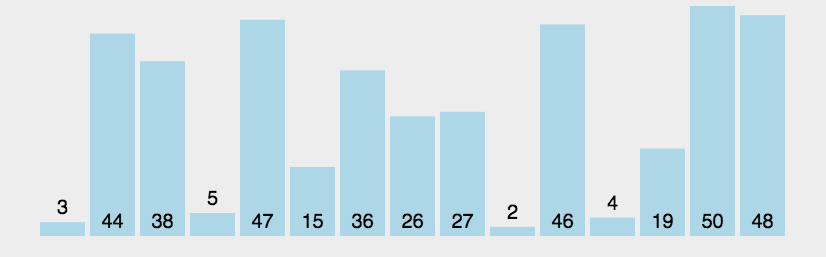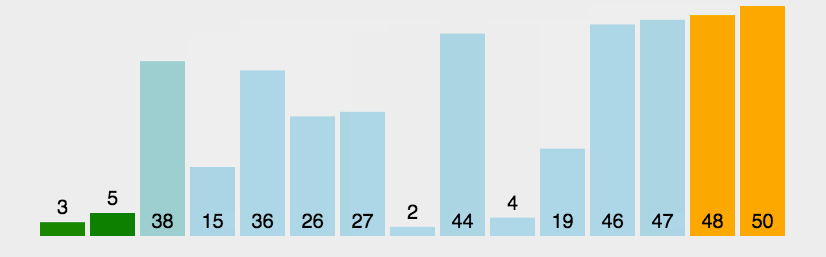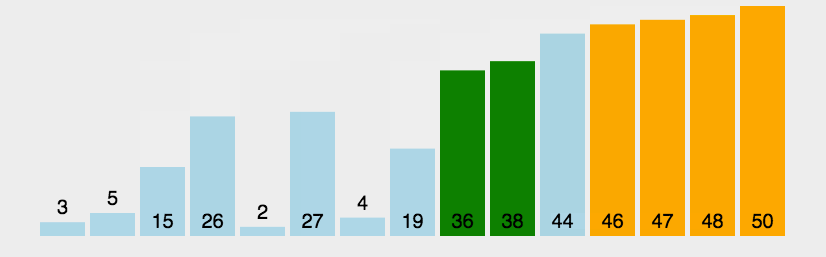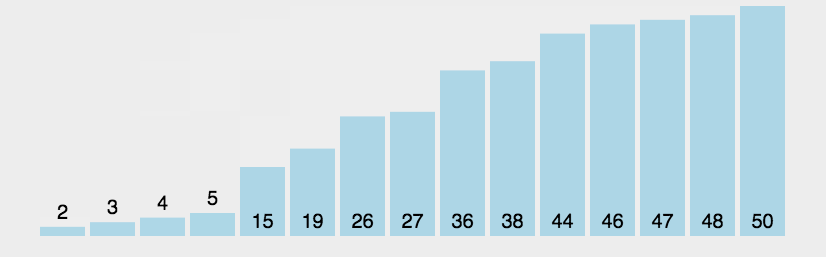
-
动图解释,后面所有的动图颜色代表的意思一样
-
黄色的条代表已经排好序的元素;
-
绿色的代表此算法正在操作,进行比较交换的元素
-
蓝色代表还没有排序的
public class BubbleSort { public static int[] bubbleSort(int[] arr) { if (arr == null || arr.length < 2) { return arr; } int n = arr.length; // 第一层循环,每循环一次,排好一个元素,放在最右边 for (int i = 0; i < n; i++) { // 第二层循环,到右边第一个 没有排序 过元素地方结束,进行比较交换 for (int j = 0; j < n -i - 1; j++) { // 比较,大于小于号决定是按照从大到小排还是从小到大排 if (arr[j + 1] < arr[j]) { // 交换 int t = arr[j]; arr[j] = arr[j+1]; arr[j+1] = t; } } } return arr; } )
可知第二层循环是进行比较交换的核心逻辑,第一层循环用来确定排好了几个元素,决定了第二层循环的比较次数,n-i-1之所以减去一,是因为比如剩下10个元素没有排序,10个元素只有9对,需要比较九次。
-
稳定性分析
稳定。只有交换才可以改变两个元素的前后顺序,当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。如果代码交换逻辑改成
if (arr[j + 1] <= arr[j]),加了个=,那么就不稳定了。
-
时间复杂度分析
-
最好情况下,要排序的数据已经是有序的了,我们只需要进行一次冒泡操作,就可以结束了,所以最好情况时间复杂度是O(n)。
-
而最坏的情况是,要排序的数据刚好是倒序排列的,我们需要进行n次冒泡操作,所以最坏情况时间复杂度为O(n2)。
关于最好情况下只需要冒泡一次,我们可以将这个冒泡算法优化一下来更加直观的看到,
优化的根据:假如从开始的第一对到结尾的最后一对,相邻的元素之间都没有发生交换的操作,这意味着右边的元素总是大于等于左边的元素,此时的数组已经是有序的了,我们无需再对剩余的元素重复比较下去了。代码如下:
-
public void bubbleSort(int[] a, int n) { for (int i = 0; i < n; ++i) { // 提前退出冒泡循环的标志位 boolean flag = false; for (int j = 0; j < n - i - 1; ++j) { if (a[j] > a[j+1]) { // 交换 int tmp = a[j]; a[j] = a[j+1]; a[j+1] = tmp;
// 表示有数据交换 flag = true;
}
}
if (!flag) break; // 没有数据交换,提前退出
}
}
直接能看到,最好情况就是n次比较。
-(void)bubbleSequence:(NSMutableArray *)arr { //普通排序-交换次数较多 for (int i = 0; i < arr.count; ++i) { for (int j = 0; j < arr.count-1-i; ++j) { if ([arr[j+1] intValue] < [arr[j] intValue]) {
[arr exchangeObjectAtIndex:j withObjectAtIndex:j+1]; } } } //优化后算法-从第一个开始排序,空间复杂度相对更大一点 for (int i = 0; i < arr.count; ++i) { bool flag=false; //遍历数组的每一个`索引`(不包括最后一个,因为比较的是j+1) for (int j = 0; j < arr.count-1-i; ++j) { //根据索引的`相邻两位`进行`比较` if ([arr[j+1] intValue] < [arr[j] intValue]) { flag = true; [arr exchangeObjectAtIndex:j withObjectAtIndex:j+1]; } } if (!flag) { break;//没发生交换直接退出,说明是有序数组 } } //优化后算法-从最后一个开始排序 for (int i = 0; i <arr.count; ++i) { bool flag=false; //遍历数组的每一个`索引`(不包括最后一个,因为比较的是j+1) for (int j = (int)arr.count-1; j >i; --j) { //根据索引的`相邻两位`进行`比较` if ([arr[j-1] intValue] > [arr[j] intValue]) { flag = true; [arr exchangeObjectAtIndex:j withObjectAtIndex:j-1]; } } if (!flag) { break;//没发生交换直接退出,说明是有序数组 } } }
注意



