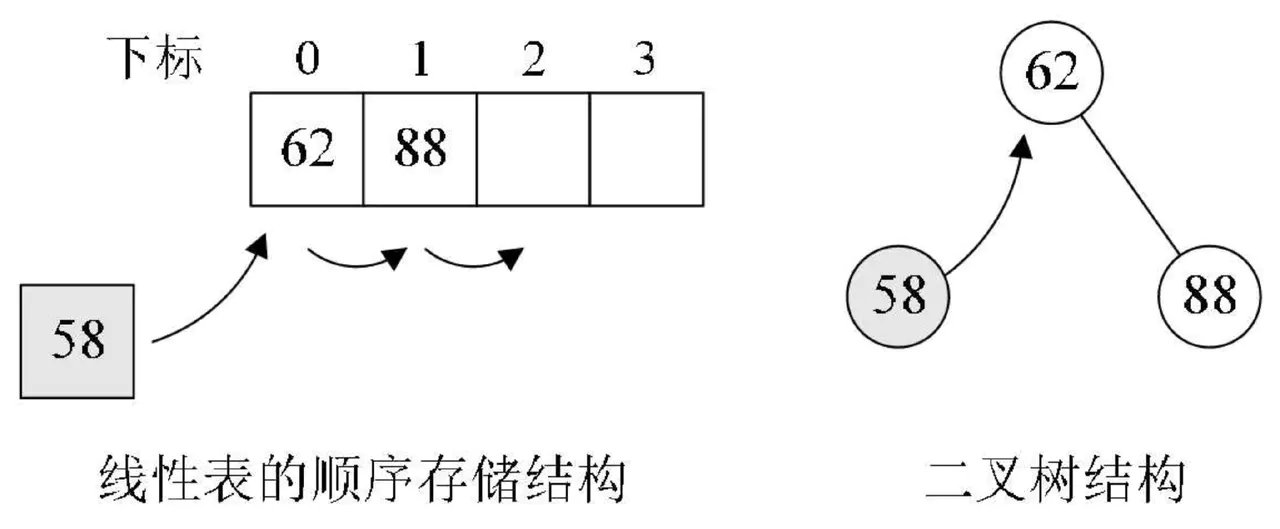
16*:查找专题静态查找以及二叉搜索树的实现:(顺序查找、折半查找、插值查找、斐波那契查找)、(二叉排序树)
问题
(顺序查找、折半查找、插值查找、斐波那契查找)、(二叉排序树)
目录
1:定义
2:顺序查找、折半查找、插值查找、斐波那契查找
3:二叉排序树
预备
正文
一:定义
查找(Searching)
就是根据给定的某个值,在査找表中确定一个其关键字等于给定值的数据元素
查找表(Search Table)
是由同一类型的数据元素(记录)构成的集合
关键字(Key)
是数据元素中某个数据项的值。又称为键值。用它可以表示一个数据元素,也可以标识一个记录的某个数据项(字段),我们称为关键码
若关键字可以唯一地标识一个记录,则称此关键字为主关键字(Primary Key)
对于那些可以识别多个属于元素(记录)的关键字,我们称为次关键字(Secondary Key)
静态查找表(Static Search Table)
只作查找操作的查找表
1. 査询某个“特定的“数据元素是否在查找表中 2. 检索某个“特定的“数据元素和各种属性
动态查找表(Dynamic Search Table)
在査找过程中同时插入查找表中不存在的数据元素,或者从查找表中删除已经存在的某个数据元素;显然动态查找表的操作就是 2 个动作
1. 查找时插入数据元素
2. 查找时删除数据元素;
二:顺序查找(Sequential Search)
又称为线性查找, 是最基本的查找技术它的查找过程:从表中的第一个(或最后一个记录开始,逐个进行记录关键字和给定值比较
1. 若某个记录的关键字和给定值相等,则查找成功,找到所查记录; 2. 如果直到最后一个(或第一个)记录,其关键字和给定值比较都不等时,则表中没有所查的记录,查找不成功
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 100 /* 存储空间初始分配量 */ typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ //1.顺序查找 //a为数组,n为查找的数组个数,key为要查找的关键字; int Sequential_Search(int *a,int n,int key){ for (int i = 1; i <= n ; i++) if (a[i] == key) return i; return 0; } //2.顺序查找_哨兵 int Sequential_Search2(int *a,int n,int key){ int i; //设置a[0]为关键字值,称为'哨兵' a[0] = key; //循环从数组尾部开始 i = n; while (a[i] != key) { i--; } //返回0,则说明查找失败 return i; } //3.折半查找算法 //假设数组a,已经是有序的(从小到大) int Binary_Search(int *a,int n,int key){ int low,high,mid; //定义最低下标为记录首位 low = 1; //定义最高下标为记录末位 high = n; while (low <= high) { //折半计算 mid = (low + high) /2; if (key < a[mid]) { //若key比a[mid] 小,则将最高下标调整到中位下标小一位; high = mid-1; }else if(key > a[mid]){ //若key比a[mid] 大,则将最低下标调整到中位下标大一位; low = mid+1; }else //若相等则说明mid即为查找到的位置; return mid; } return 0; } //4. 插值查找 int Interpolation_Search(int *a,int n,int key){ int low,high,mid; low = 1; high = n; while (low <= high) { //插值 mid = low+ (high-low)*(key-a[low])/(a[high]-a[low]); if (key < a[mid]) { //若key比a[mid]插值小,则将最高下标调整到插值下标小一位; high = mid-1; }else if(key > a[mid]){ //若key比a[mid]插值 大,则将最低下标调整到插值下标大一位; low = mid+1; }else //若相等则说明mid即为查找到的位置; return mid; } return 0; } //5.斐波拉契查找 int F[100]; /* 斐波那契数列 */ int Fibonacci_Search(int *a,int n,int key){ int low,high,mid,i,k; //最低下标为记录的首位; low = 1; //最高下标为记录的末位; high = n; k = 0; //1.计算n为斐波拉契数列的位置; while (n > F[k]-1) { k++; } //2.将数组a不满的位置补全值; for(i = n;i < F[k]-1;i++) a[i] = a[n]; //3. while (low <= high) { //计算当前分隔的下标; mid = low+F[k-1]-1; if (key < a[mid]) { //若查找的记录小于当前分隔记录; //将最高下标调整到分隔下标mid-1处; high = mid-1; //斐波拉契数列下标减1位; k = k-1; }else if(key > a[mid]){ //若查找的记录大于当前的分隔记录; //最低下标调整到分隔下标mid+1处 low = mid+1; //斐波拉契数列下标减2位; k = k-2; }else{ if (mid <= n) { //若相等则说明,mid即为查找的位置; return mid; }else { //若mid>n,说明是补全数值,返回n; return n; } } } return 0; } int main(int argc, const char * argv[]) { // insert code here... printf("Hello, 静态查找!\n\n"); int a[MAXSIZE+1],i,result; int arr[MAXSIZE] = {0,1,16,24,35,47,59,62,73,88,99}; for (i = 0; i<= MAXSIZE; i++) { a[i] = i; } //1,顺序查找 result=Sequential_Search(a,MAXSIZE,MAXSIZE); printf("顺序查找:%d\n",result); //2,顺序查找_哨兵 result=Sequential_Search2(a,MAXSIZE,1); printf("顺序查找_哨兵:%d \n",result); //3.折半查找 result=Binary_Search(arr,10,62); printf("折半查找:%d \n",result); //4.插值查找 result=Interpolation_Search(arr,10,62); printf("插值查找:%d \n",result); //5.斐波拉契查找 //斐波拉契数列计算; F[0]=0; F[1]=1; for(i = 2;i < 100;i++) { F[i] = F[i-1] + F[i-2]; } result=Fibonacci_Search(arr,10,99); printf("斐波拉契查找:%d \n",result); result=Fibonacci_Search(arr,10,59); printf("斐波拉契查找:%d \n",result); printf("\n"); return 0; }
1:顺序查找
顺序查找(Sequential Search), ⼜又称为线性查找. 是最基本的查找技术. 它的查找过程: 从表中的第一个(或最后一个)记录开始,逐个进⾏行行记录关键 字和给定值⽐比较;
1:若某个记录的关键字和给定值相等,则查找成功,找到所查记录;
2:如果直到最后⼀一个(或第⼀一个)记录, 其关键字和给定值⽐比较都不不等 时, 则表中没有所查的记录,查找不不成功;
2:折半查找(Binary Search)
又称为二分查找,它的前提是线性表中的记录必须是关键码有序(通常是从小到大有序)线性表必须采用顺序存储
思想:
在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等则查找成功;
若给定值小于中间的记录关键字,则在中间记录的左半区继续査找
若给定的值大于中间记录的关键字,则在中间记录的右半区继续查找,不断重复以上的过程,直到査找成功,或所以查找区域无记录,查找失败为止。
3:插值查找



条件: (1)数据必须采用顺序存储结构;(2)数据必须有序。 原理: (1)最接近查找长度的斐波那契值来确定拆分点;(2)黄金分割。
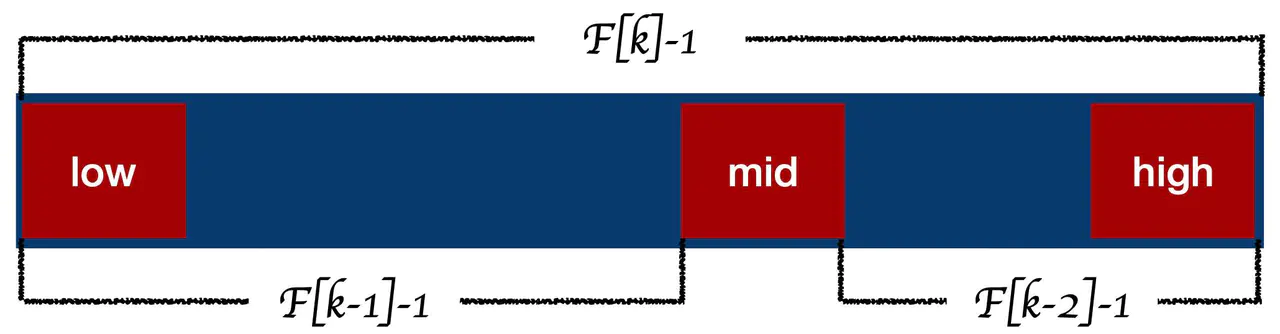
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,即n=F(k)-1; 开始将key值与黄金分割点的值,即第 F(k-1)位置的记录进行比较(mid=low+F(k-1)-1),比较结果也分为三种 1)相等,mid位置的元素即为所求 2)> ,low=mid+1,k-=2;说明:low=mid+1说明待查找的元素在[mid+1,hign]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找 3)< ,high=mid-1,k-=1;说明:high=mid-1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归的应用斐波那契查找
5:顺序查找-总结
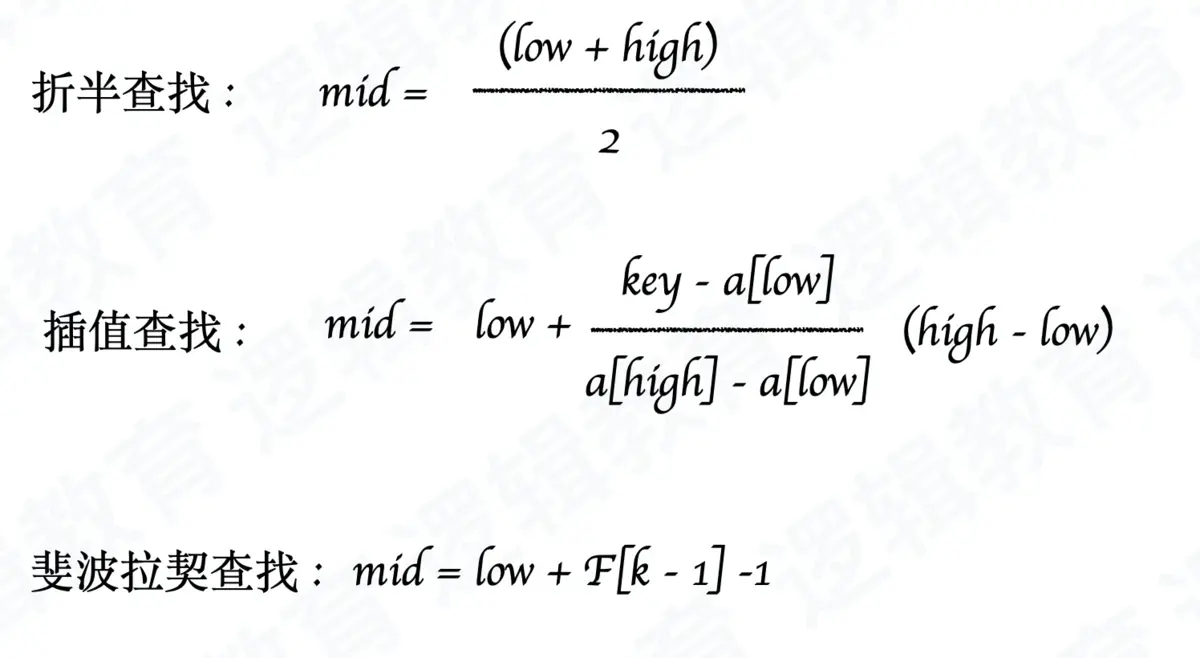
三:二叉排序树
1:定义
又称为二叉查找树或者二叉搜索树,它或者是一颗空树。或者是一颗具有下列性质的二叉树
- 1.若它的左子树不空,则左子树上所有结点的值均小于它的根结构的值
- 2.若它的右子树不空,则右子树上的所有结点的值均大于它的根结点的值
- 3.它的左右子树也分别是二叉排序树
2:构建二叉排序树
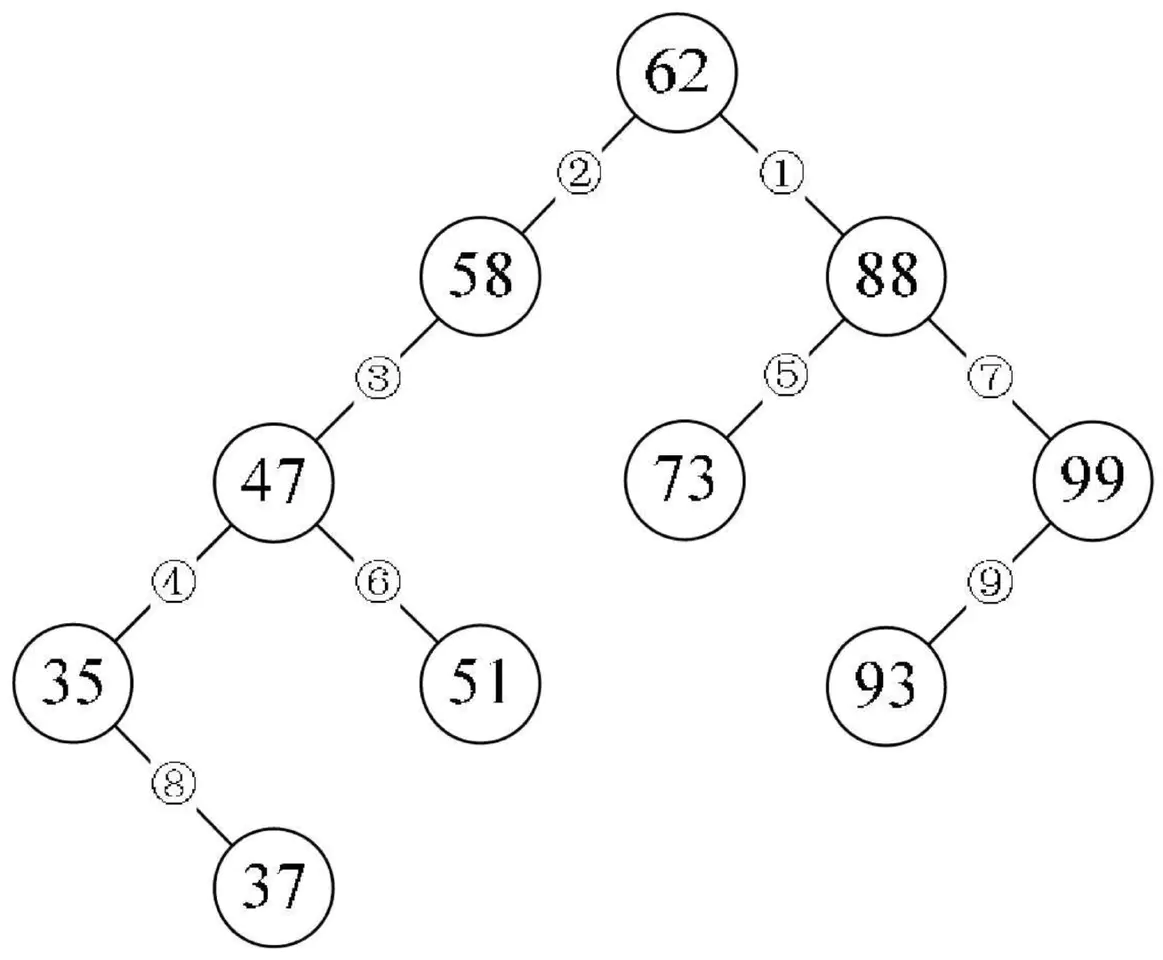
这样我们就得到了一棵二叉树,并且当我们对它进行中序遍历时,就可以得到一个有序的序列{35,37,47,51,58,62,73,88,93,99},所以我们通常称它为二叉排序树。
二叉排序树(Binary Sort Tree),又称为二叉查找树。它或者是一棵空树,或者是具有下列性质的二叉树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结构的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
从二叉排序树的定义也可以知道,它前提是二叉树,然后它采用了递归的定义方法,再者,它的结点间满足一定的次序关系,左子树结点一定比其双亲结点小,右子树结点一定比其双亲结点大。
构造一棵二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除关键字的速度。不管怎么说,在一个有序数据集上的查找,速度总是要快于无序的数据集的,而二叉排序树这种非线性的结构,也有利于插入和删除的实现。
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 100 typedef int Status; //二叉树的二叉链表结点结构定义 //结点结构 typedef struct BiTNode { //结点数据 int data; //左右孩子指针 struct BiTNode *lchild, *rchild; } BiTNode, *BiTree; //1.二叉排序树--查找 /* 递归查找二叉排序树T中,是否存在key; 指针f指向T的双亲,器初始值为NULL; 若查找成功,则指针p指向该数据元素的结点,并且返回TRUE; 若指针p指向查找路径上访问的最后一个结点则返回FALSE; */ Status SearchBST(BiTree T,int key,BiTree f, BiTree *p){ if (!T) /* 查找不成功 */ { *p = f; return FALSE; } else if (key==T->data) /* 查找成功 */ { *p = T; return TRUE; } else if (key<T->data) return SearchBST(T->lchild, key, T, p); /* 在左子树中继续查找 */ else return SearchBST(T->rchild, key, T, p); /* 在右子树中继续查找 */ } //2.二叉排序树-插入 /* 当二叉排序树T中不存在关键字等于key的数据元素时, */ /* 插入key并返回TRUE,否则返回FALSE */ Status InsertBST(BiTree *T, int key) { BiTree p,s; //1.查找插入的值是否存在二叉树中;查找失败则-> if (!SearchBST(*T, key, NULL, &p)) { //2.初始化结点s,并将key赋值给s,将s的左右孩子结点暂时设置为NULL s = (BiTree)malloc(sizeof(BiTNode)); s->data = key; s->lchild = s->rchild = NULL; //3. if (!p) { //如果p为空,则将s作为二叉树新的根结点; *T = s; }else if(key < p->data){ //如果key<p->data,则将s插入为左孩子; p->lchild = s; }else //如果key>p->data,则将s插入为右孩子; p->rchild = s; return TRUE; } return FALSE; } //3.从二叉排序树中删除结点p,并重接它的左或者右子树; Status Delete(BiTree *p){ BiTree temp,s; if((*p)->rchild == NULL){ //情况1: 如果当前删除的结点,右子树为空.那么则只需要重新连接它的左子树; //①将结点p临时存储到temp中; temp = *p; //②将p指向到p的左子树上; *p = (*p)->lchild; //③释放需要删除的temp结点; free(temp); }else if((*p)->lchild == NULL){ //情况2:如果当前删除的结点,左子树为空.那么则只需要重新连接它的右子树; //①将结点p存储到temp中; temp = *p; //②将p指向到p的右子树上; *p = (*p)->rchild; //③释放需要删除的temp结点 free(temp); }else{ //情况③:删除的当前结点的左右子树均不为空; //①将结点p存储到临时变量temp, 并且让结点s指向p的左子树 temp = *p; s = (*p)->lchild; //②将s指针,向右到尽头(目的是找到待删结点的前驱) //-在待删除的结点的左子树中,从右边找到直接前驱 //-使用`temp`保存好直接前驱的双亲结点 while (s->rchild) { temp = s; s = s->rchild; } //③将要删除的结点p数据赋值成s->data; (*p)->data = s->data; //④重连子树 //-如果temp 不等于p,则将S->lchild 赋值给temp->rchild //-如果temp 等于p,则将S->lchild 赋值给temp->lchild if(temp != *p) temp->rchild = s->lchild; else temp->lchild = s->lchild; //⑤删除s指向的结点; free(s) free(s); } return TRUE; } //4.查找结点,并将其在二叉排序中删除; /* 若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素结点, */ /* 并返回TRUE;否则返回FALSE。 */ Status DeleteBST(BiTree *T,int key) { //不存在关键字等于key的数据元素 if(!*T) return FALSE; else { //找到关键字等于key的数据元素 if (key==(*T)->data) return Delete(T); else if (key<(*T)->data) //关键字key小于当前结点,则缩小查找范围到它的左子树; return DeleteBST(&(*T)->lchild,key); else //关键字key大于当前结点,则缩小查找范围到它的右子树; return DeleteBST(&(*T)->rchild,key); } } int main(int argc, const char * argv[]) { // insert code here... printf("Hello, 二叉排序树(Binary Sort Tree)!\n"); int i; int a[10]={62,88,58,47,35,73,51,99,37,93}; BiTree T=NULL; for(i=0;i<10;i++) { InsertBST(&T, a[i]); } BiTree p; int statusValue = SearchBST(T, 99, NULL, &p); printf("查找%d是否成功:%d (1->YES/0->NO)\n",p->data,statusValue); statusValue = DeleteBST(&T,93); printf("二叉排序树删除93是否成功:%d (1->YES/0->NO)\n",statusValue); statusValue = DeleteBST(&T,47); printf("二叉排序树删除47是否成功:%d (1->YES/0->NO)\n",statusValue); statusValue = DeleteBST(&T,12); printf("二叉排序树删除12是否成功:%d (1->YES/0->NO)\n",statusValue); statusValue = SearchBST(T, 93, NULL, &p); printf("查找%d是否成功:%d (1->YES/0->NO)\n",93,statusValue); statusValue = SearchBST(T, 47, NULL, &p); printf("查找%d是否成功:%d (1->YES/0->NO)\n",47,statusValue); statusValue = SearchBST(T, 99, NULL, &p); printf("查找%d是否成功:%d (1->YES/0->NO)\n",99,statusValue); printf("\n"); return 0; }
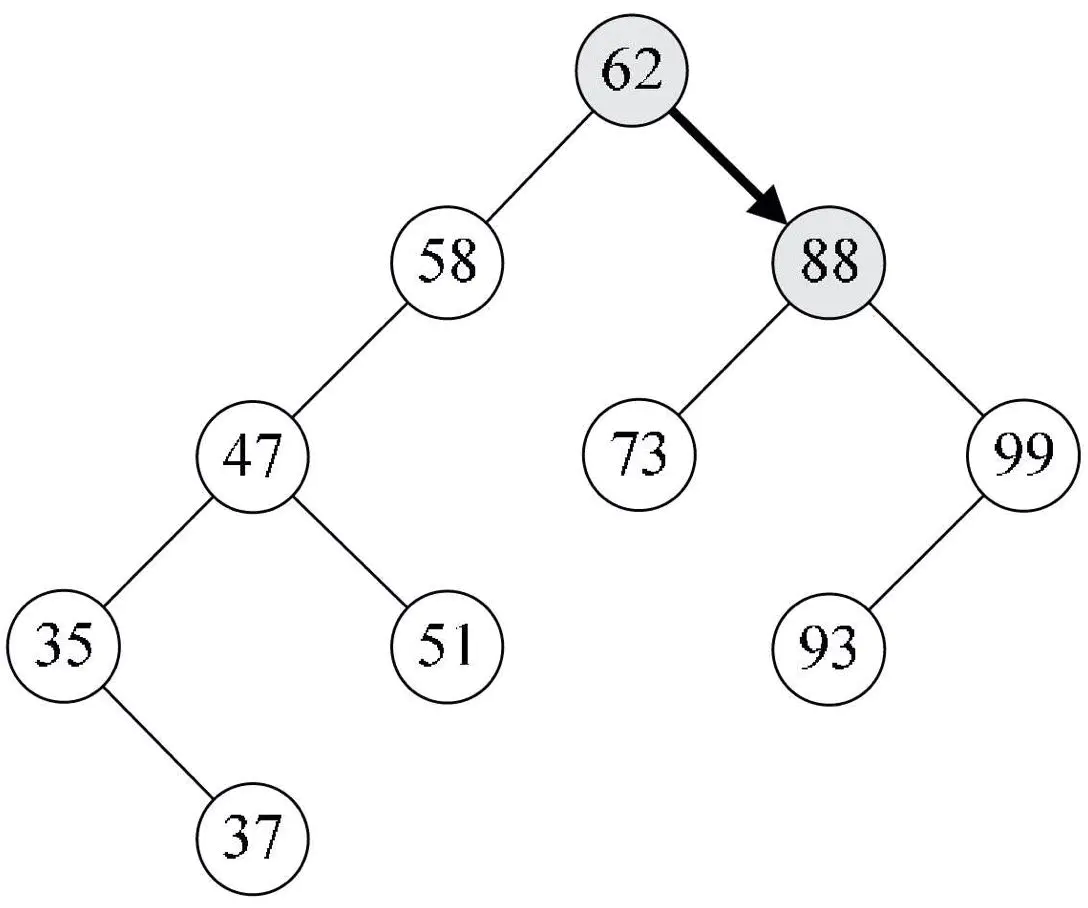
1:二叉排序树查找操作
1.SearchBST函数是一个可递归运行的函数,函数调用时的语句为SearchBST(T,93,NULL,p),参数T是一个二叉链表,其中数据如上图所示,key代表要查找的关键字,目前我们打算查找93,二叉树f指向T的双亲,当T指向根结点时,f的初值就为NULL,它在递归时有用,最后的参数p是为了查找成功后可以得到查找到的结点位置。
2.第3~7行,是用来判断当前二叉树是否到叶子结点,显然图8-6-3告诉我们当前T指向根结点62的位置,T不为空,第5~6行不执行。
3.第8~12行是查找到相匹配的关键字时执行语句,显然93≠62,第10~11行不执行。
4.第13~14行是当要查找关键字小于当前结点值时执行语句,由于93>62,第14行不执行。
5.第15~16行是当要查找关键字大于当前结点值时执行语句,由于93>62,所以递归调用SearchBST(T->rchild,key,T,p)。此时T指向了62的右孩子88,如下图所示。
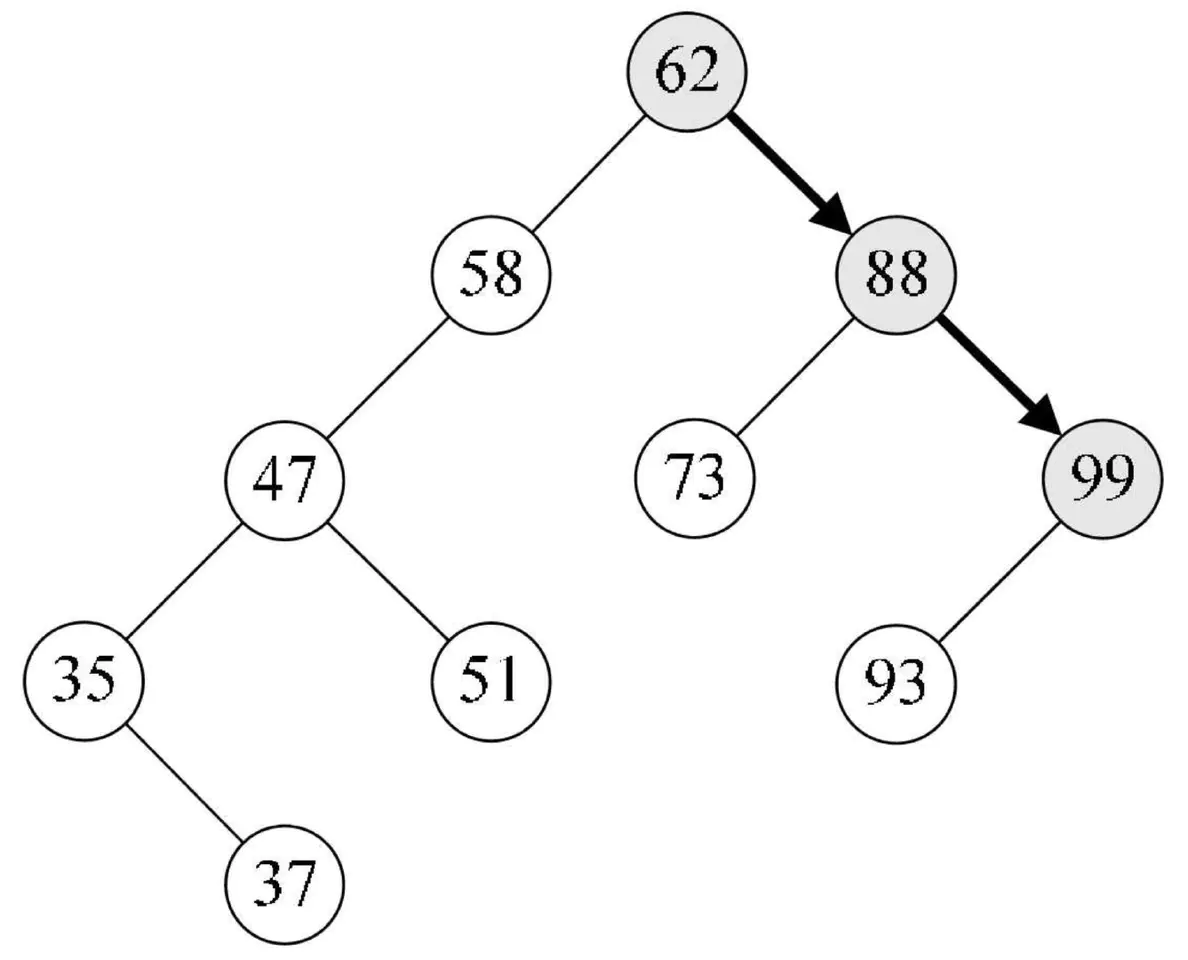
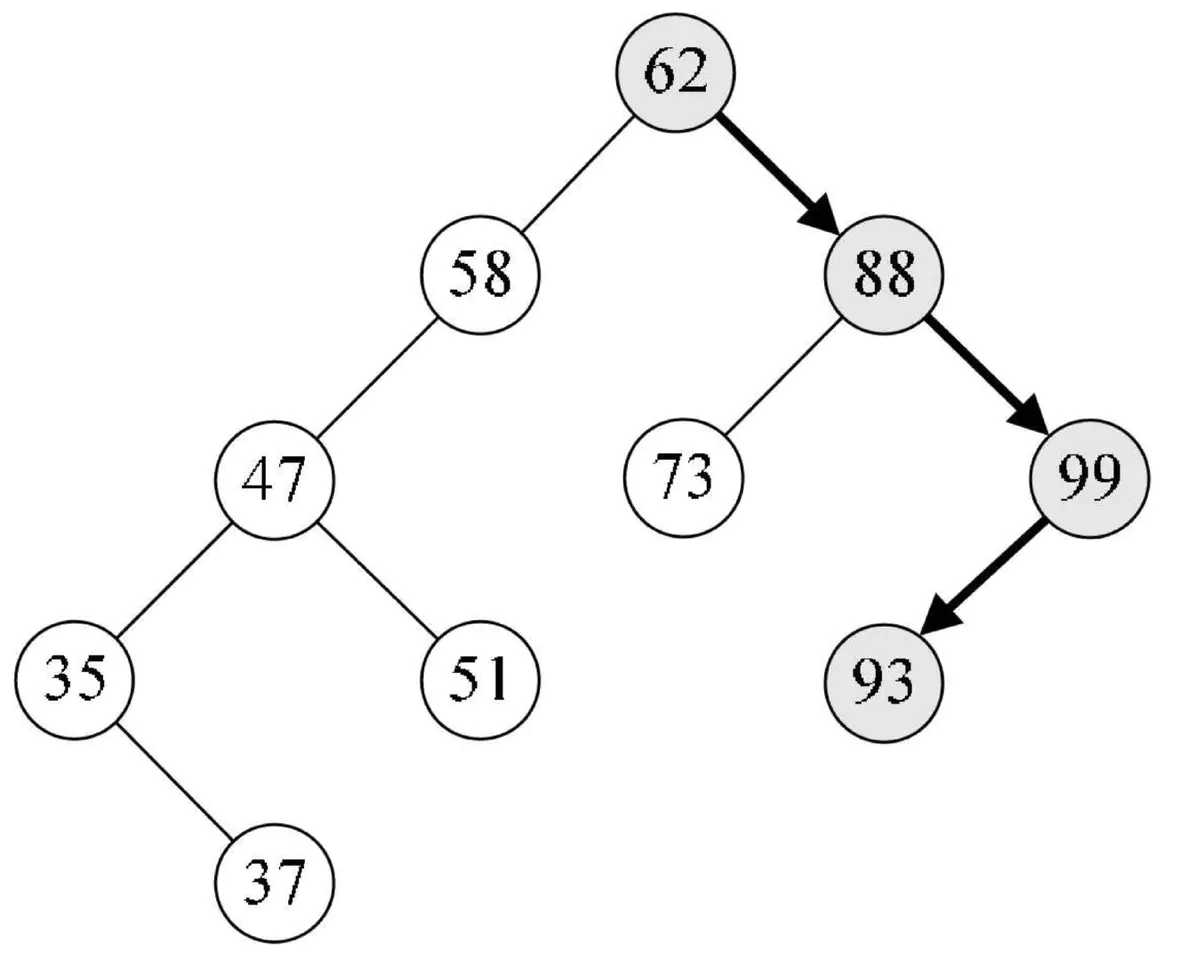
2:二叉排序树插入操作
有了二叉排序树的查找函数,那么所谓的二叉排序树的插入,其实也就是将关键字放到树中的合适位置而已,
这段代码非常简单。如果你调用函数是“In-sertBST(&T,93);”,那么结果就是FALSE,如果是“InsertBST(&T,95);”,那么一定就是在93的结点增加一个右孩子95,并且返回True。如下图所示。
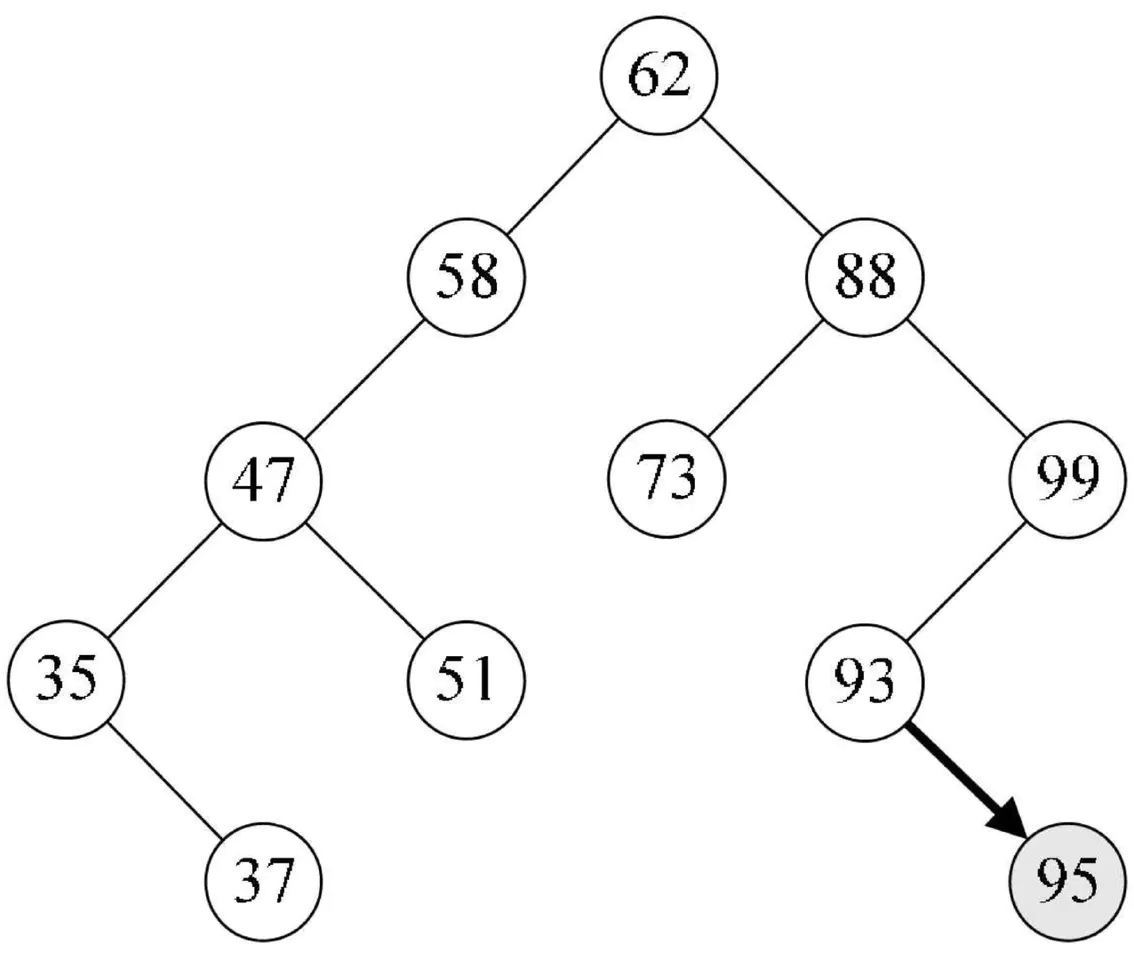
有了二叉排序树的插入代码,我们要实现二叉排序树的构建就非常容易了。下面的代码就可以创建一棵二叉树。
int i; int a[10] = { 62, 88, 58, 47, 35, 73, 51, 99, 37, 93 }; BiTree T = NULL; for (i = 0; i < 10; i++) { InsertBST(&T, a[i]); }
3:二叉排序树删除操作
俗话说“请神容易送神难”,我们已经介绍了二叉排序树的查找与插入算法,但是对于二叉排序树的删除,就不是那么容易,我们不能因为删除了结点,而让这棵树变得不满足二叉排序树的特性,所以删除需要考虑多种情况。
如果需要查找并删除如37、51、73、93这些在二叉排序树中是叶子的结点,那是很容易的,毕竟删除它们对整棵树来说,其他结点的结构并未受到影响,如下图所示。
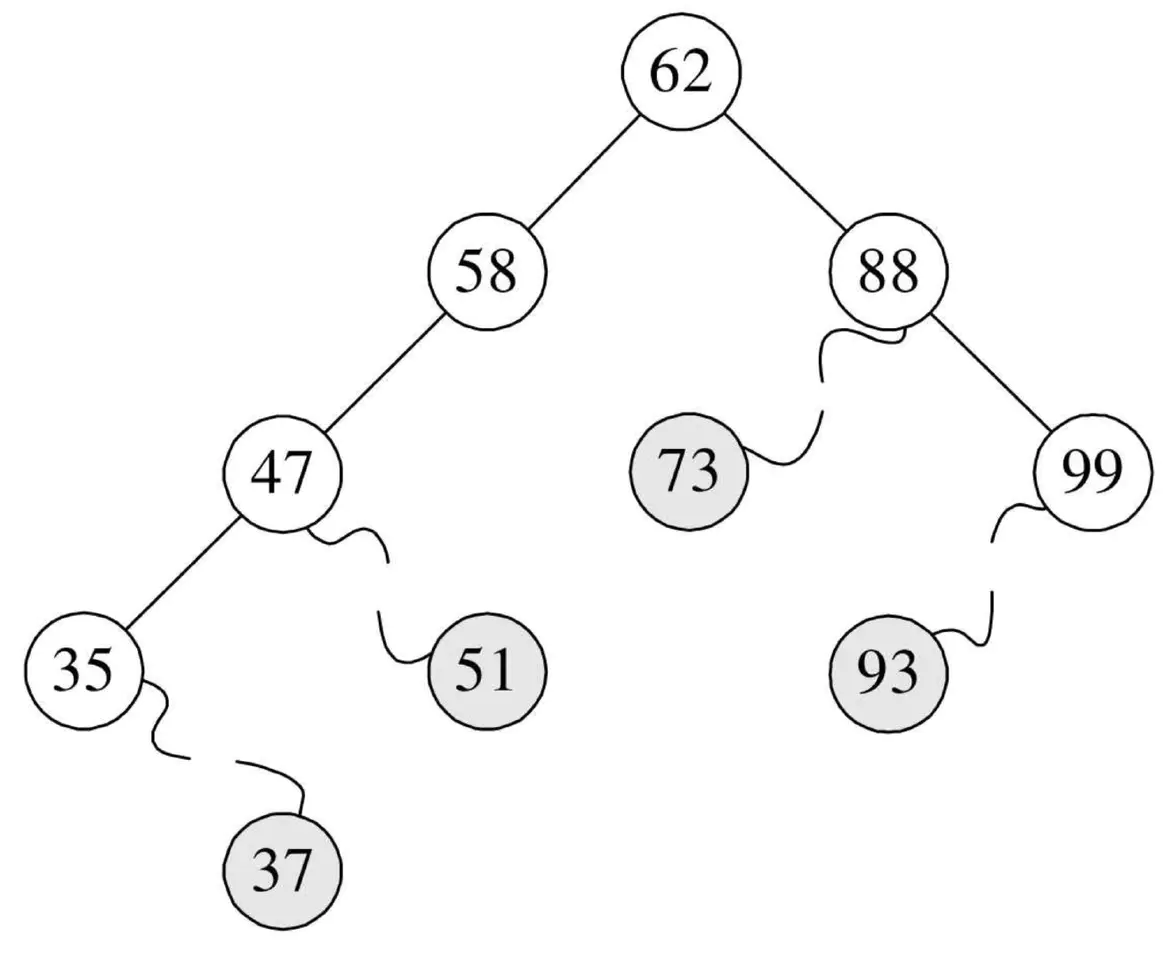
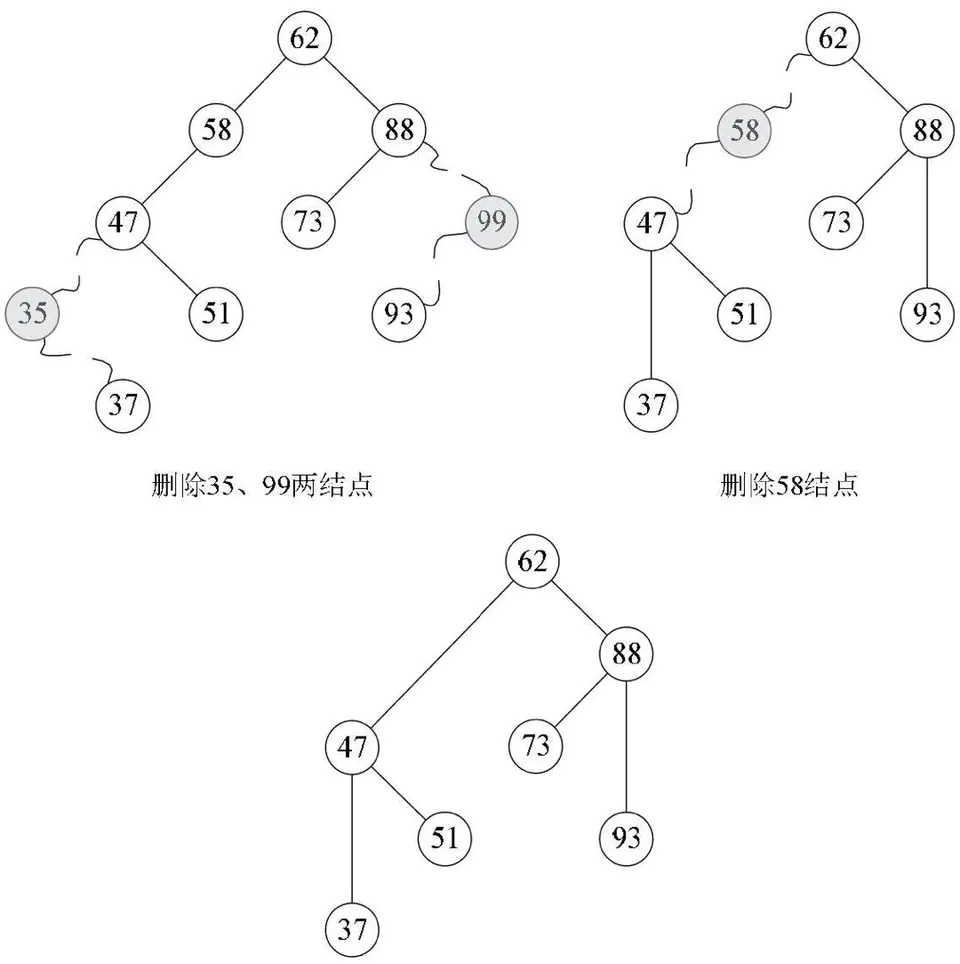
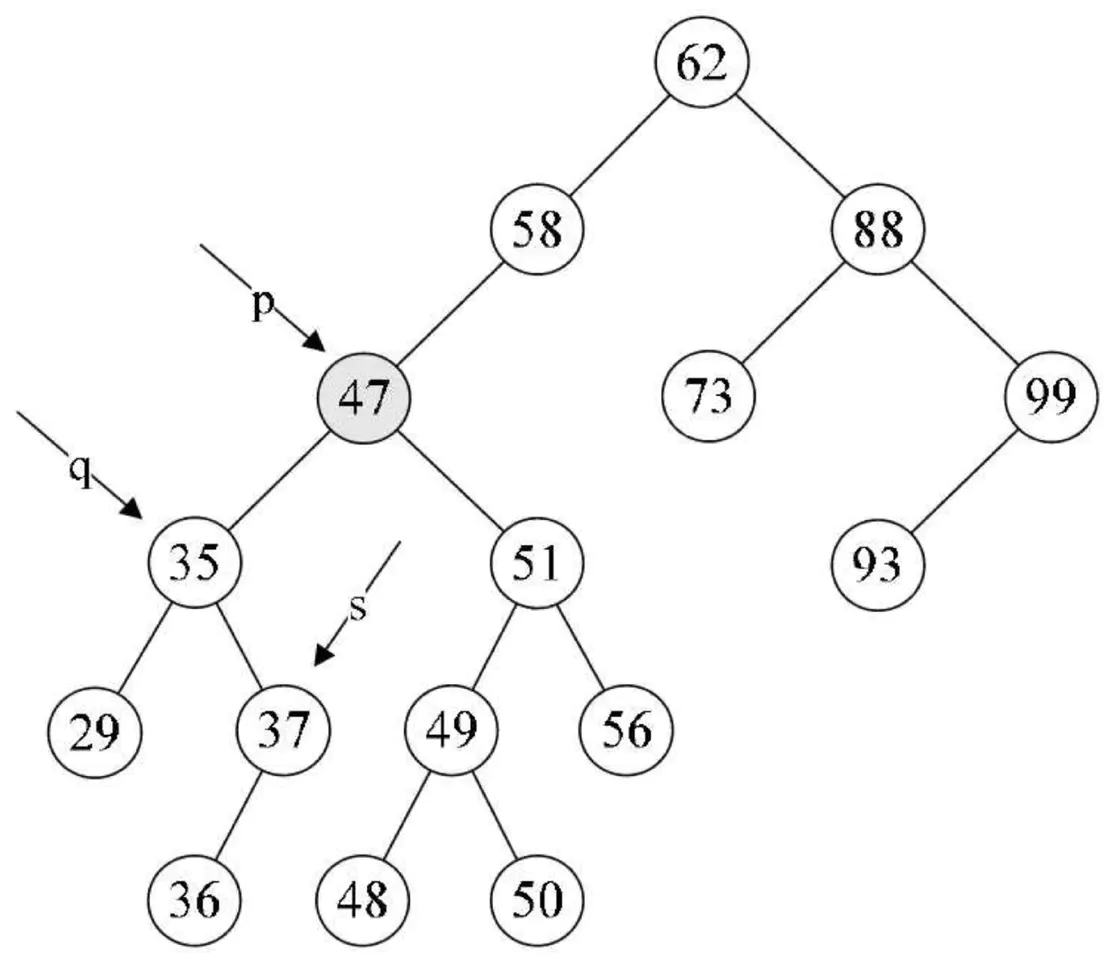
但是对于要删除的结点既有左子树又有右子树的情况怎么办呢?比如下图中的47结点若要删除了,它的两儿子以及子孙们怎么办呢?
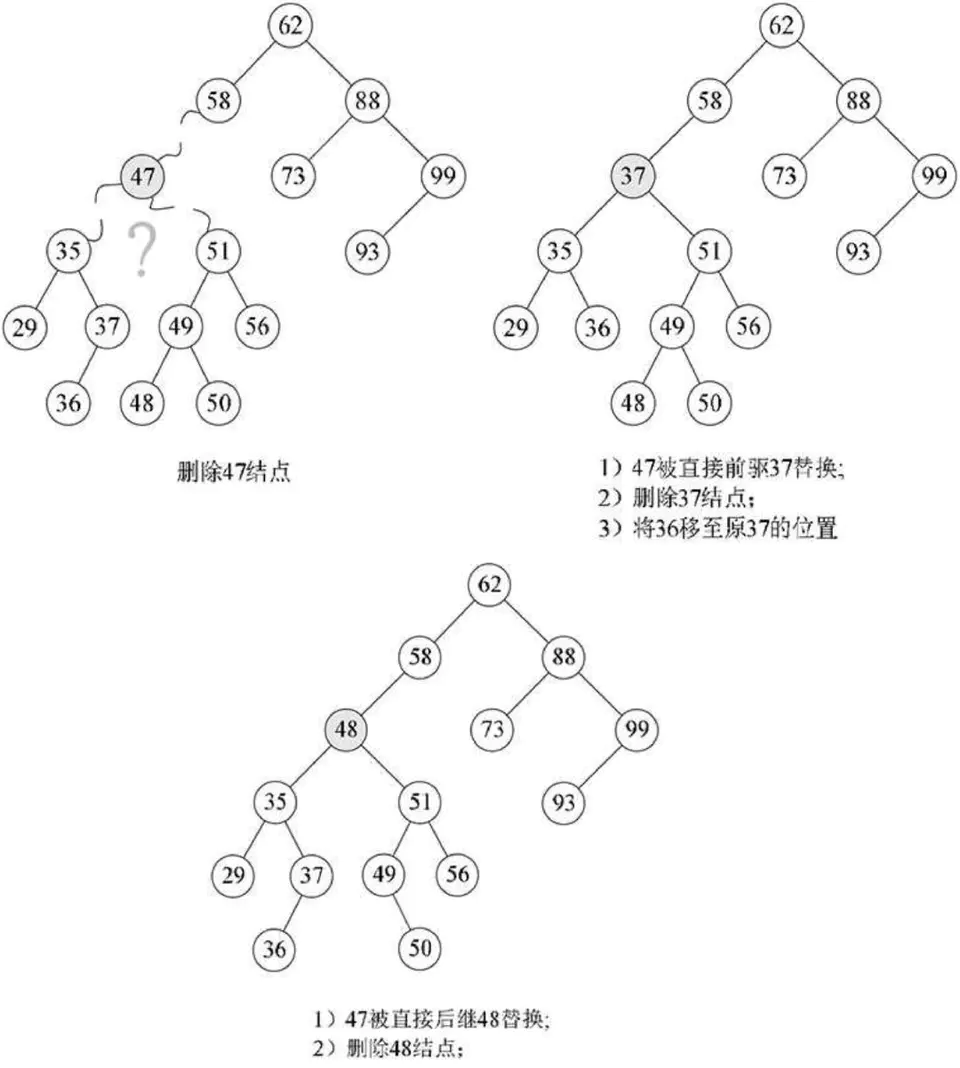
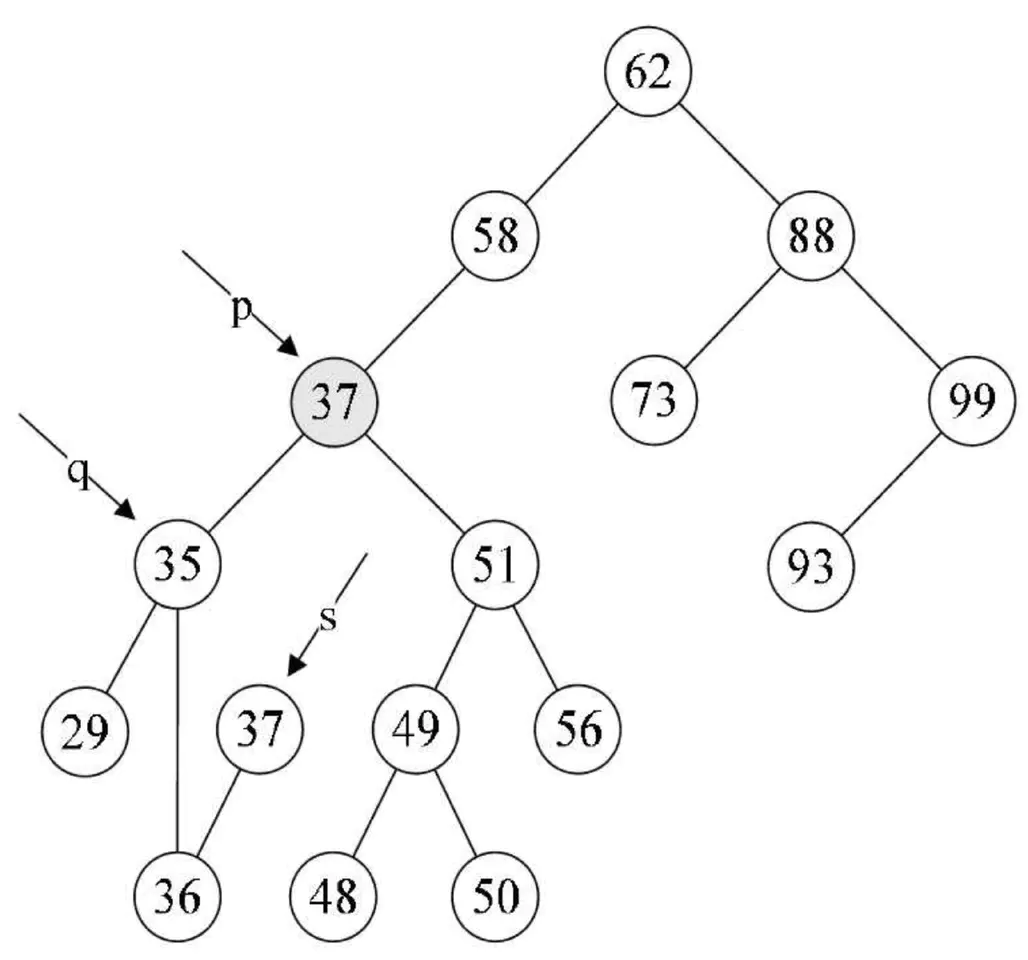
我们仔细观察一下,47的两个子树中能否找出一个结点可以代替47呢?果然有,37或者48都可以代替47,此时在删除47后,整个二叉排序树并没有发生什么本质的改变。
为什么是37和48?对的,它们正好是二叉排序树中比它小或比它大的最接近47的两个数。也就是说,如果我们对这棵二叉排序树进行中序遍历,得到的序列{29,35,36,37,47,48,49,50,51,56,58,62,73,88,93,99},它们正好是47的前驱和后继。
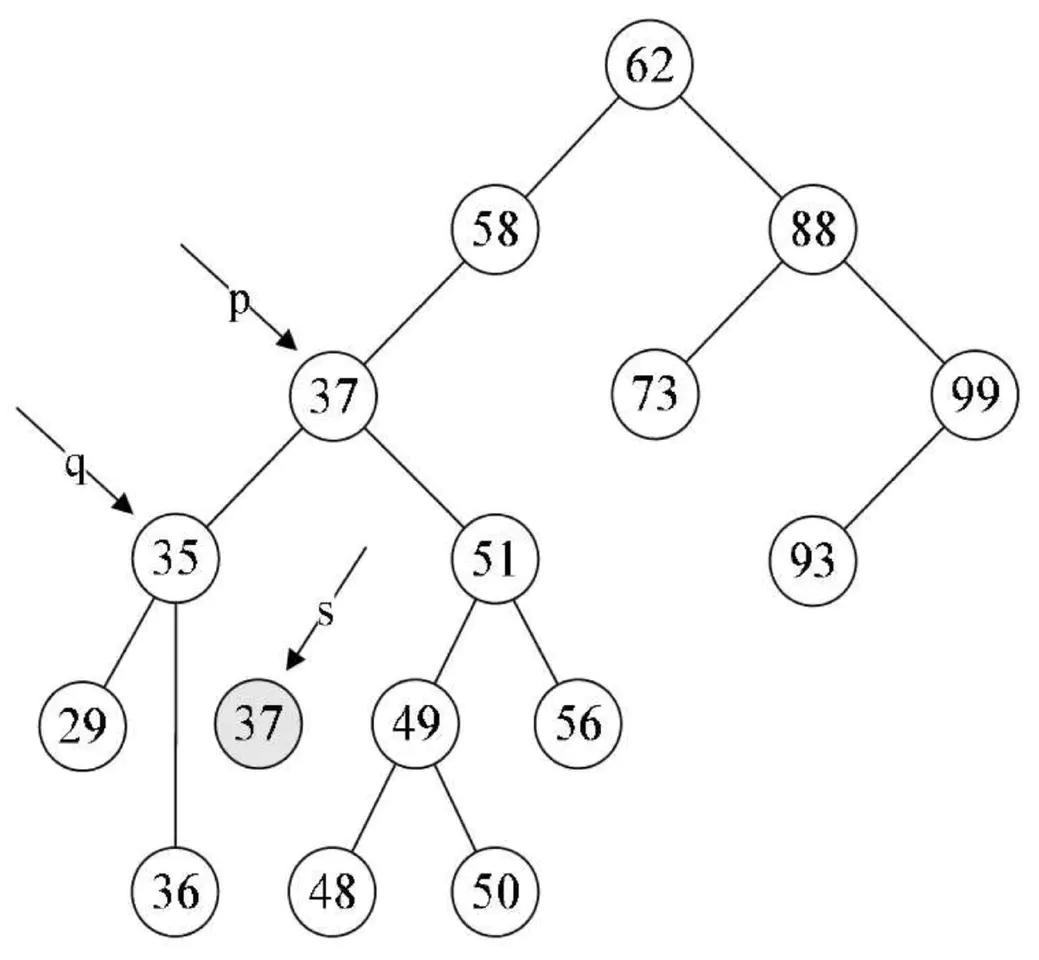
因此,比较好的办法就是,找到需要删除的结点p的直接前驱(或直接后继)s,用s来替换结点p,然后再删除此结点s,如下图所示。
根据我们对删除结点三种情况的分析:
- 叶子结点;
- 仅有左或右子树的结点;
- 左右子树都有的结点,我们来看代码,下面这个算法是递归方式对二叉排序树T查找key,查找到时删除。
1.程序开始执行,代码第4~7行目的是为了删除没有右子树只有左子树的结点。此时只需将此结点的左孩子替换它自己,然后释放此结点内存,就等于删除了。
2.代码第8~11行是同样的道理处理只有右子树没有左子树的结点删除问题。
3.第12~25行处理复杂的左右子树均存在的问题。
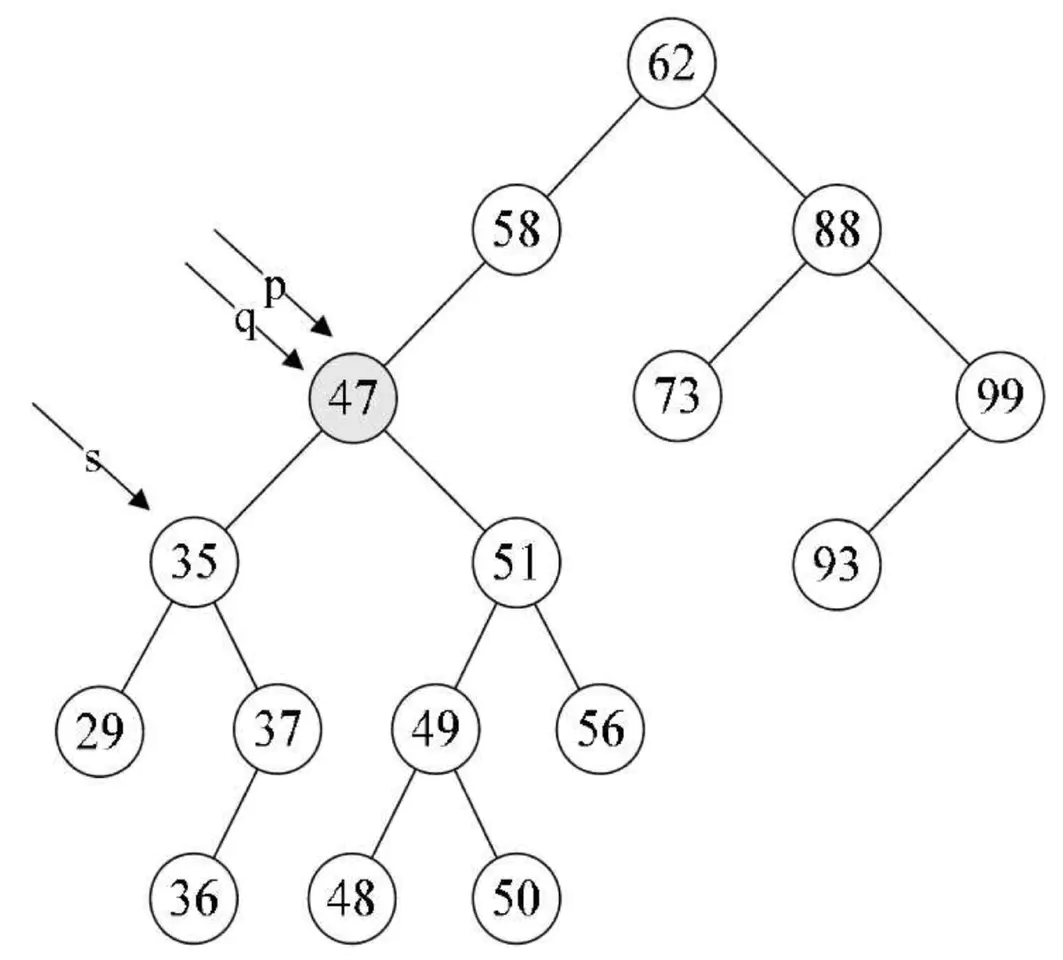
4.第14行,将要删除的结点p赋值给临时的变量q,再将p的左孩子p->lchild赋值给临时的变量s。此时q指向47结点,s指向35结点,如下图所示。
总结
总之,二叉排序树是以链接的方式存储,保持了链接存储结构在执行插入或删除操作时不用移动元素的优点,只要找到合适的插入和删除位置后,仅需修改链接指针即可。插入删除的时间性能比较好。而对于二叉排序树的查找,走的就是从根结点到要查找的结点的路径,其比较次数等于给定值的结点在二叉排序树的层数。极端情况,最少为1次,即根结点就是要找的结点,最多也不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状。可问题就在于,二叉排序树的形状是不确定的。
例如{62,88,58,47,35,73,51,99,37,93}这样的数组,我们可以构建如下图左图的二叉排序树。但如果数组元素的次序是从小到大有序,如{35,37,47,51,58,62,73,88,93,99},则二叉排序树就成了极端的右斜树,注意它依然是一棵二叉排序树,如图8-6-18的右图。此时,同样是查找结点99,左图只需要两次比较,而右图就需要10次比较才可以得到结果,二者差异很大。
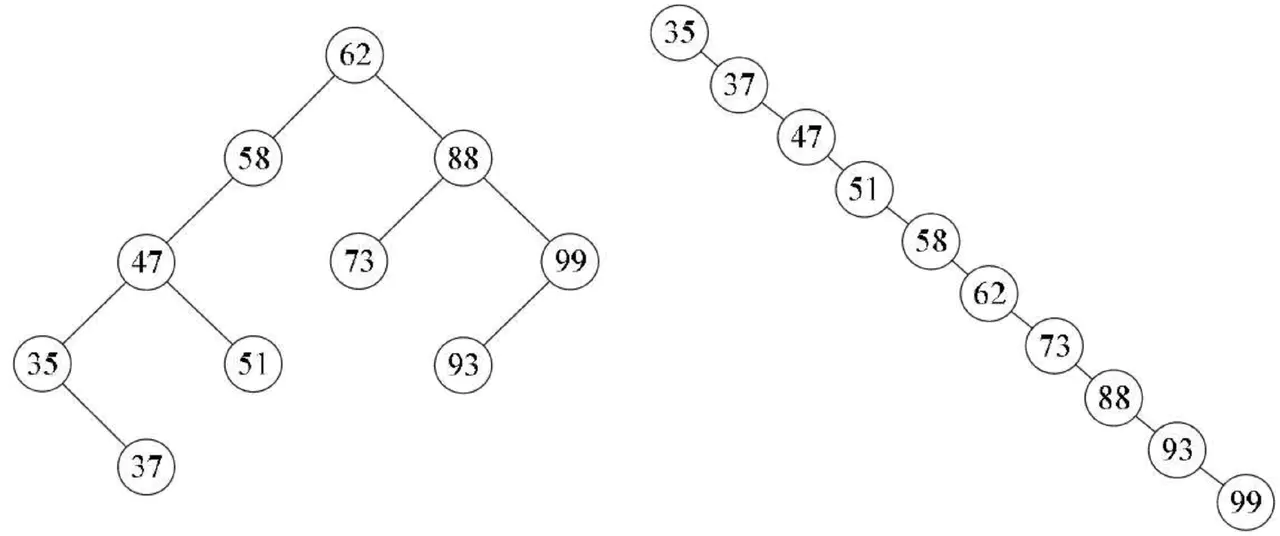
也就是说,我们希望二叉排序树是比较平衡的,即其深度与完全二叉树相同,均为,那么查找的时间复杂也就为O(logn),近似于折半查找,事实上,上图的左图也不够平衡,明显的左重右轻。
不平衡的最坏情况就是像上图右图的斜树,查找时间复杂度为O(n),这等同于顺序查找。
因此,如果我们希望对一个集合按二叉排序树查找,最好是把它构建成一棵平衡的二叉排序树。这样我们就引申出另一个问题,如何让二叉排序树平衡的问题。
注意