13*:图的应用:最小生成树普里姆(Prim)算法、克鲁斯卡尔(Kruskal)算法:(通图生成树、设计一个最小成本的⽹网络布线路线、最小生成树普里姆(Prim)算法、克鲁斯卡尔(Kruskal)算法)
问题
1:普里姆(Prim)算法
typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph;
2:克鲁斯卡尔(Kruskal)算法
typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; /* 对边集数组Edge结构的定义 */ typedef struct { int begin; int end; int weight; }Edge ;
目录
1:通图生成树
2:设计一个最小成本的⽹网络布线路线
3:最小生成树普里姆(Prim)算法
4:克鲁斯卡尔(Kruskal)算法
预备
正文
一:了解连通图生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。 [1]最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
所谓⼀个连通图的⽣成树是一个极⼩的连通子图,它含有图中全部的n个顶点,但只足以构成一颗树的n-1条边
1:连通图的生成树的判断
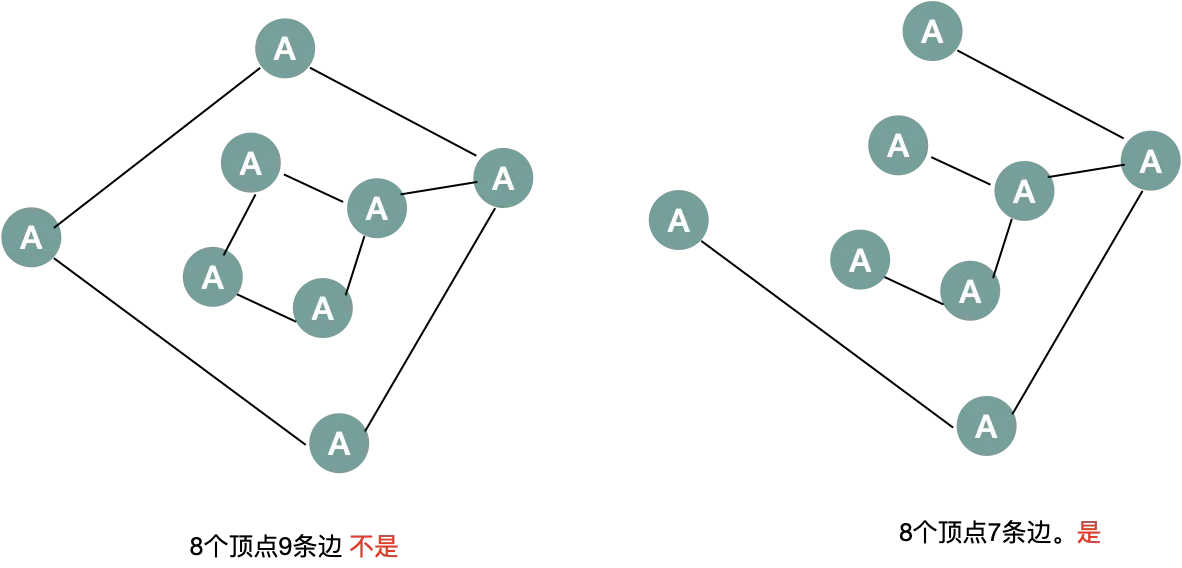
2:连通图生成树的三个条件
满⾜足以下3个条件则为连通图的⽣生成树:
• 图是连通图;
• 图中包含了了N个顶点;
• 图中边的数量量等于N-1条边.
3:最小生成树问题解析
最⼩生成树: 把构成连通⽹网的最⼩代价的生成树称为最⼩生成树
prim算法适合稠密图,kruskal算法适合简单图
我们通过一道阿里的算法面试题分析:
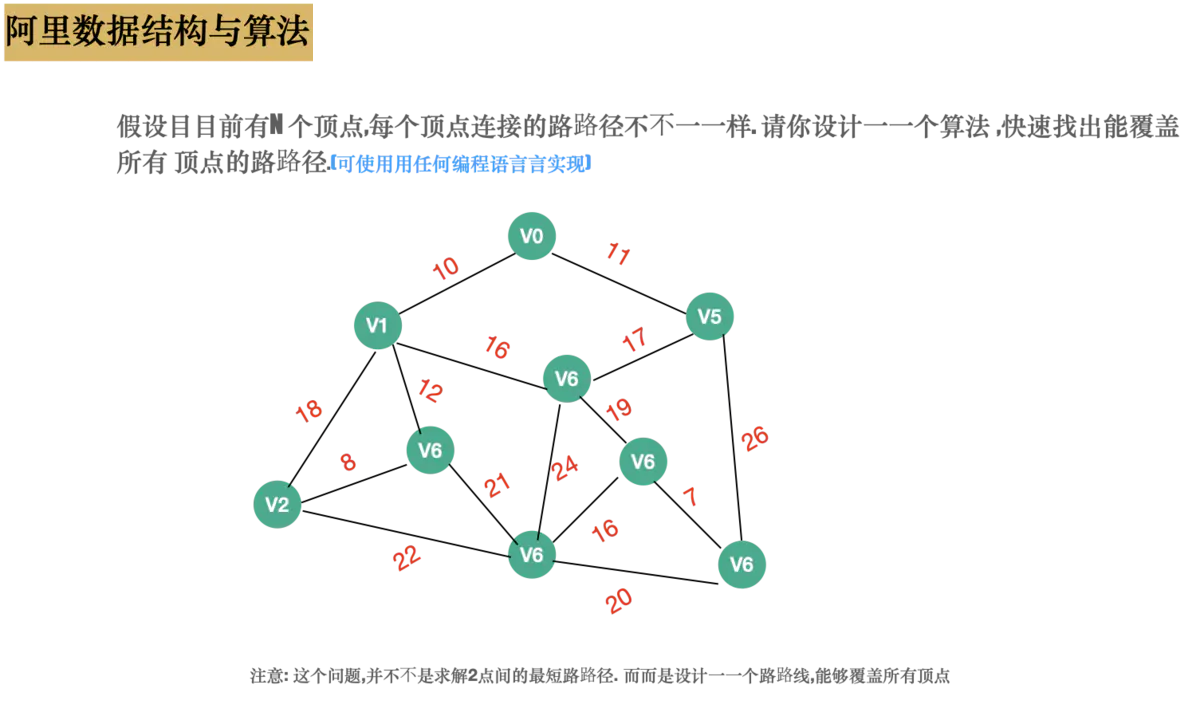
二:设计一个最小成本的⽹网络布线路线
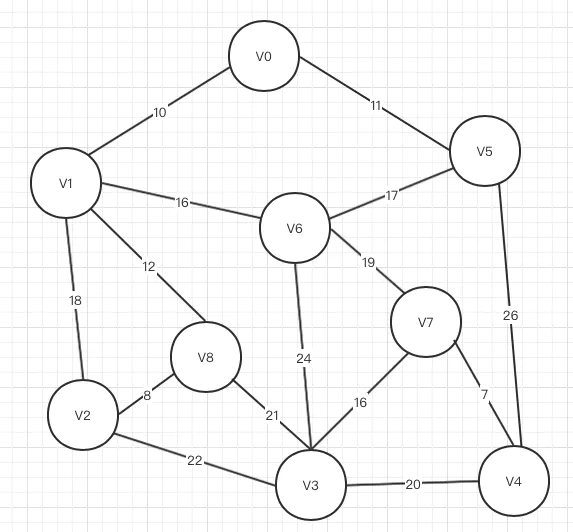
1:先把所有的顶点和顶点之间的边用邻接矩阵存储,顶点与顶点之间有连接的存储权值,没有存储一个无穷大的值
会发现因为是无向图,所以所有的的权值是以主对角线对称
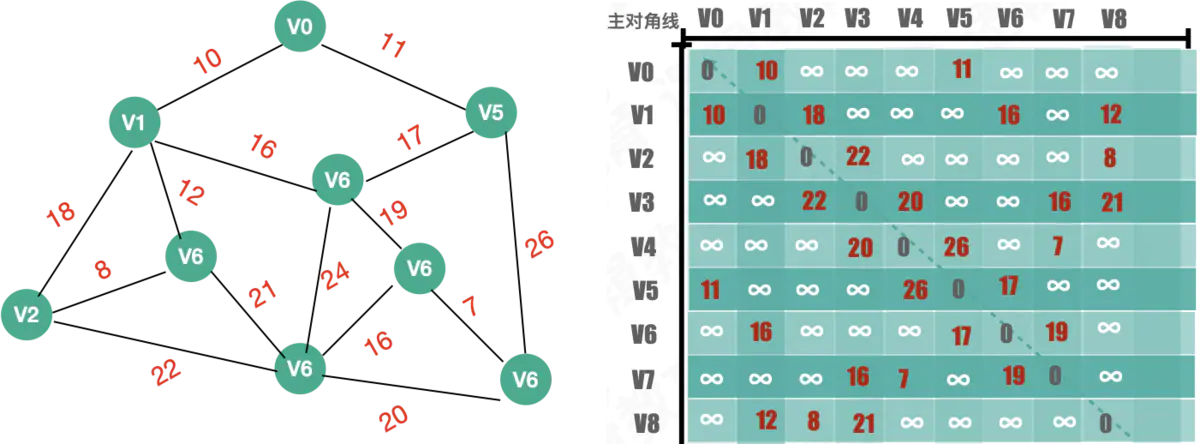
并且把arjvex[1~8]都赋值为0. 表示都是与顶点V0 相关的顶 点.
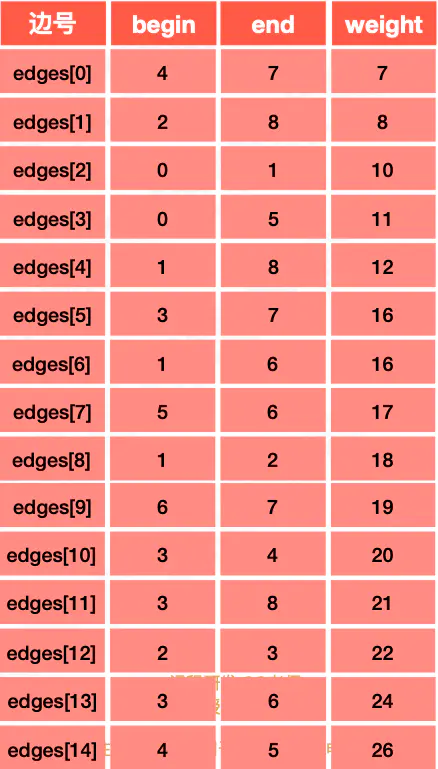
| 序号 | 图 | 可选择的路线(所有可以选择的路线) | 最终选择的路线(根据权值的大小)选择权值小的 |
| 1 | 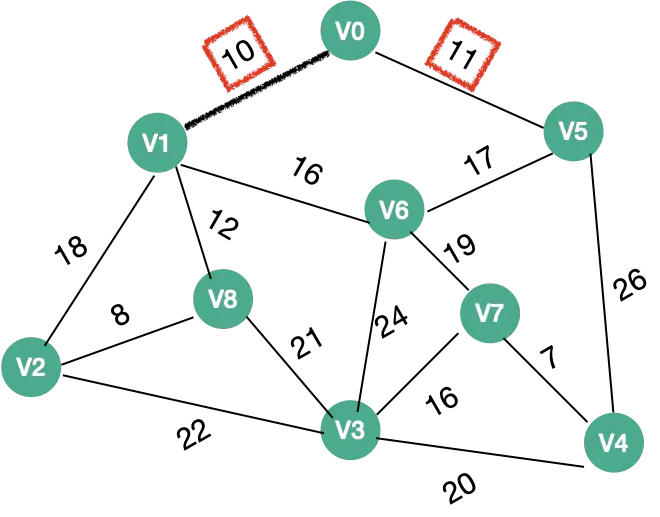 |
V1 、V5 | V1 权值:10 |
| 2 | 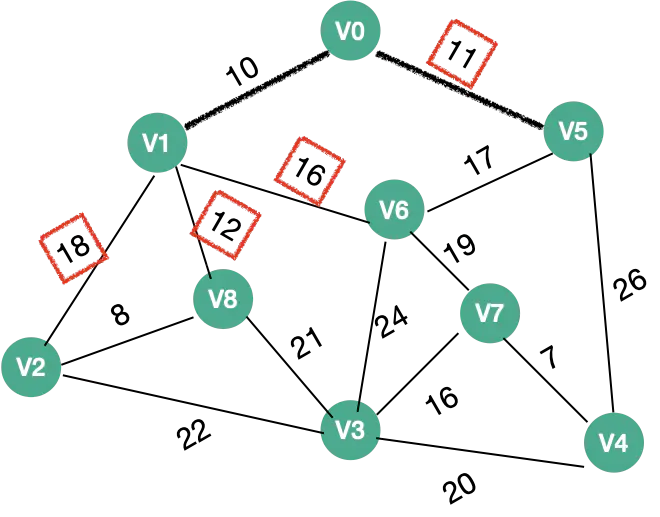 |
V2 、V8、V5 、V6 | V5权值:11 |
| 3 | 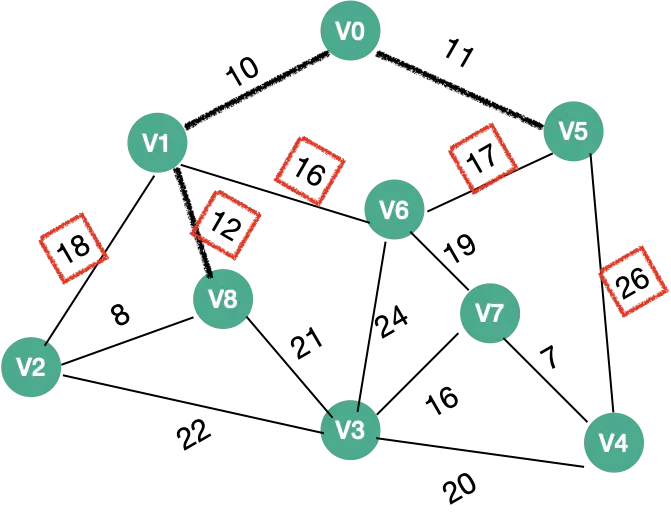 |
V2 、V3、V7 、V6 、V4 | V8权值:12 |
| 4 | 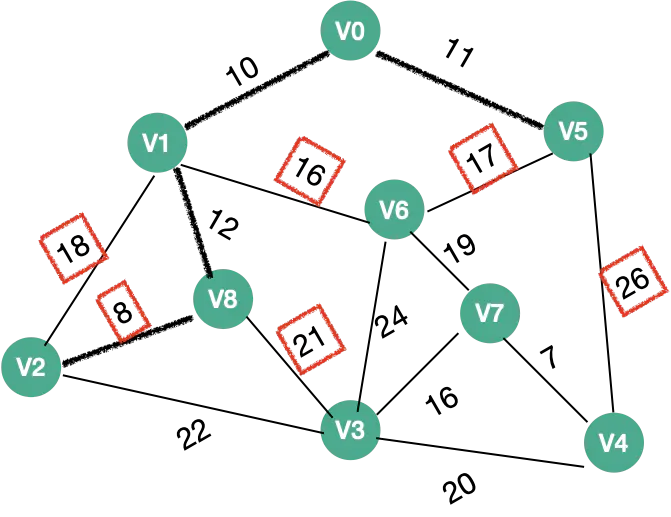 |
V2 、V3、V4 、V6 | V2权值:8 |
| 5 | 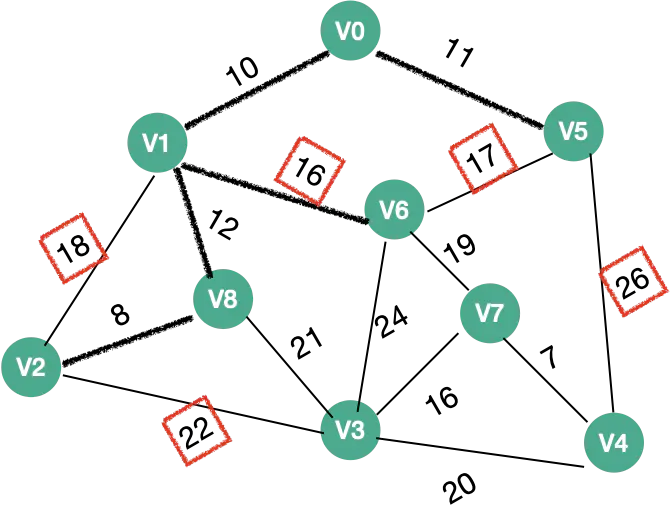 |
V1、V7 、V6 | V6权值:16 |
| 6 | 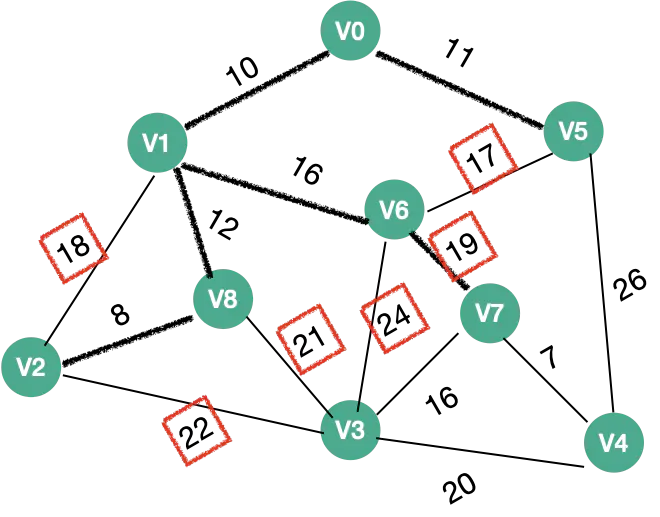 |
V1 、V3、V7 、V5 18和17 不能走如果走了这两条路的话 ,会形成闭环 | V7权值:19 |
| 7 | 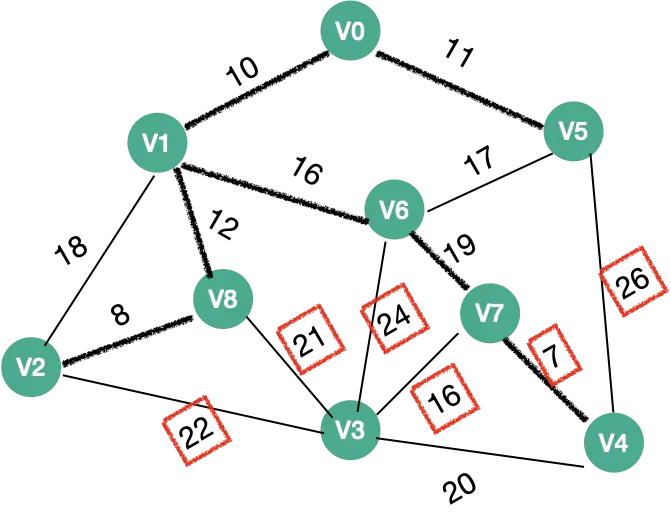 |
V4 、V3 | V4权值:7 |
| 8 |  |
V4 、V3 | V3权值:16 |
三:最小生成树Prim算法解析与实现
普里姆(Prim)算法思路
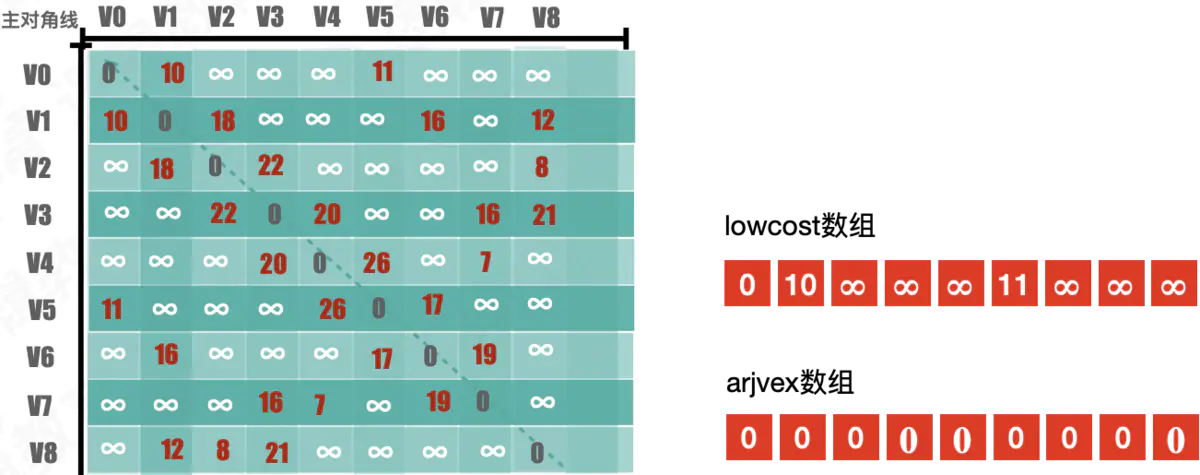
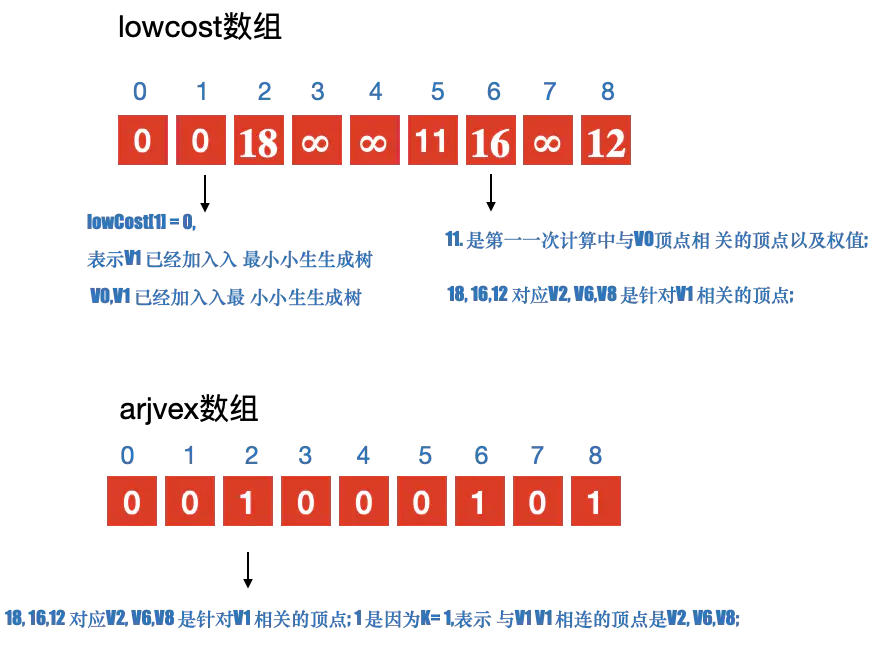
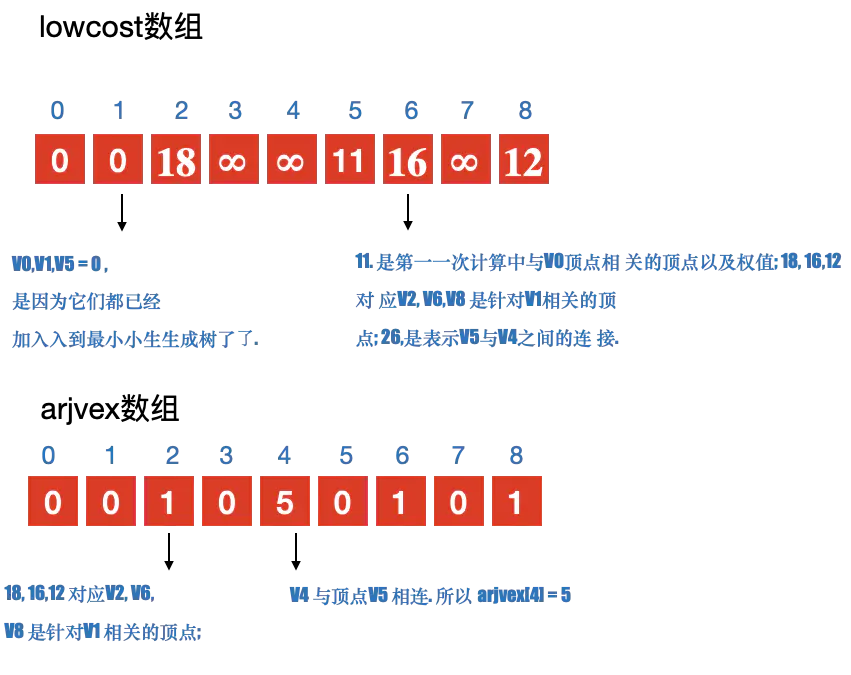
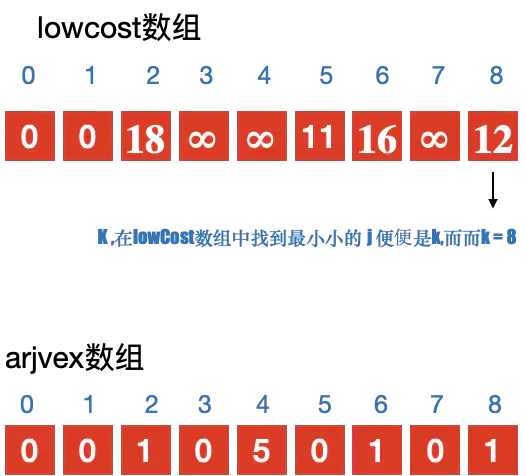
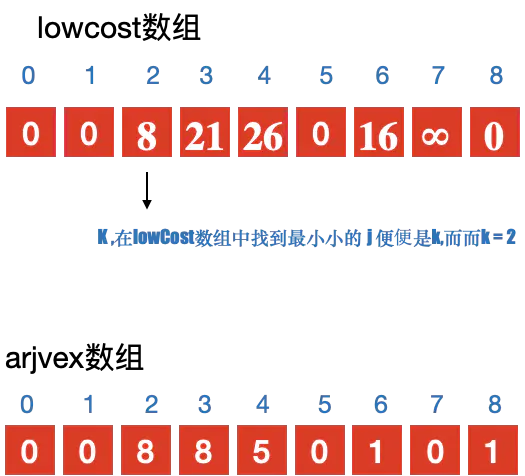
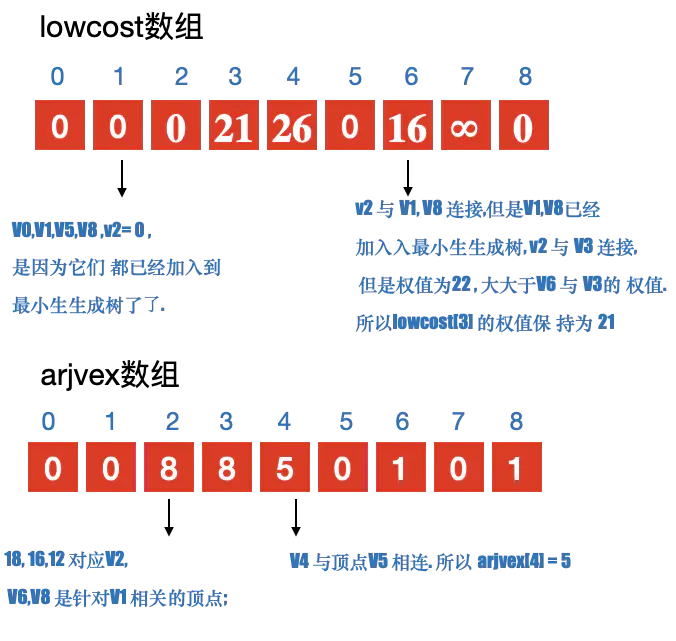
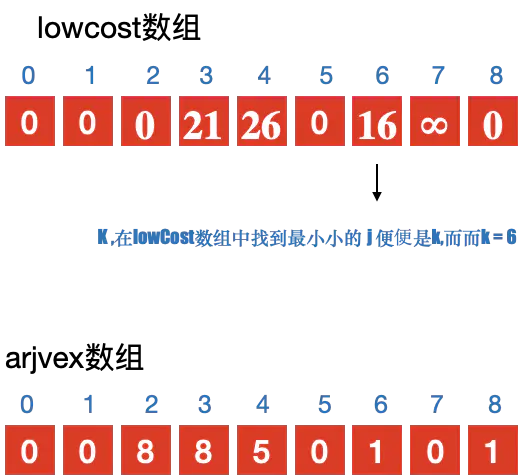
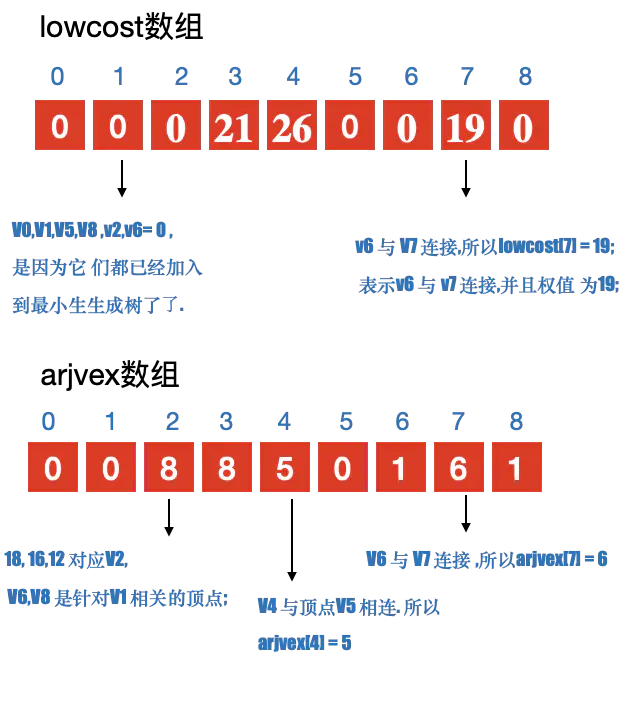
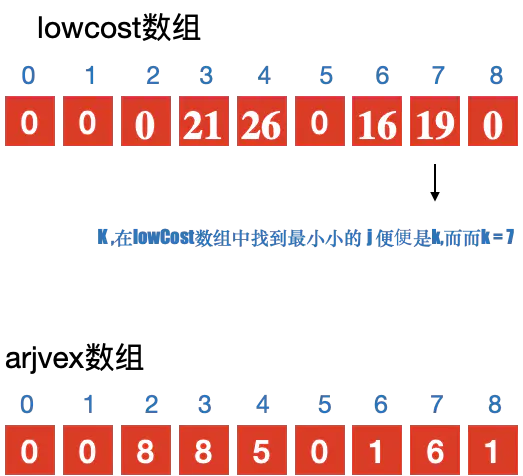
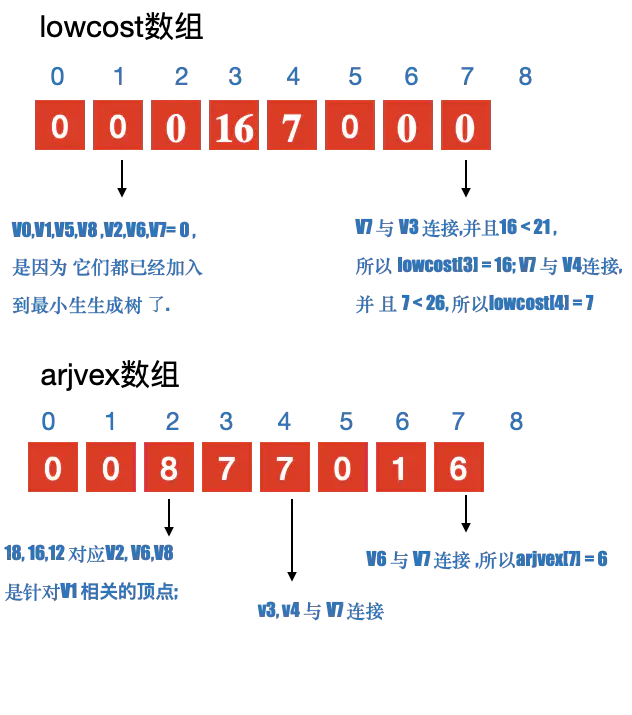
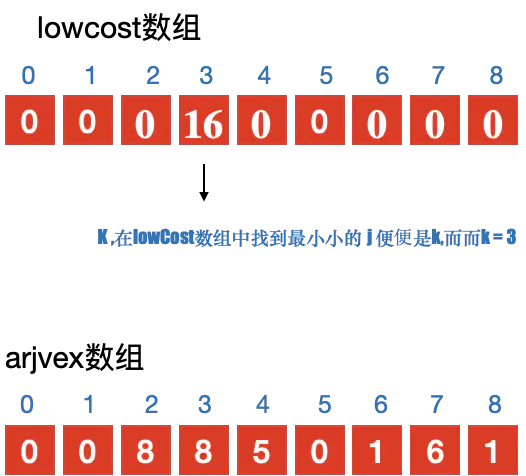
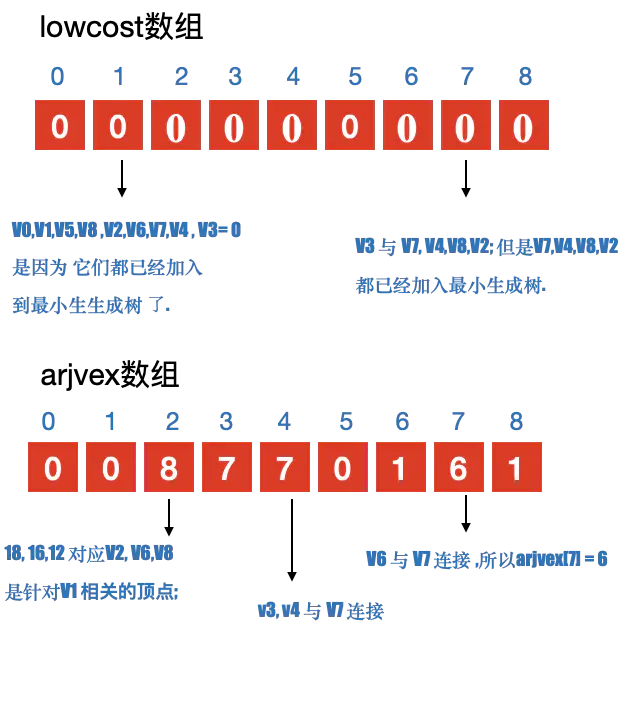
- 定义2个数组; adjvex ⽤用来保存相关顶点下标; lowcost 保存顶点之间的权值
- 初始化2个数组, 从v0开始寻找最⼩小⽣生成树, 默认v0是最⼩小⽣生成树上第一个顶点 3. 循环lowcost 数组,根据权值,找到顶点 k;
- 更新lowcost 数组
- 循环所有顶点,找到与顶点k 有关系的顶点. 并更新lowcost 数组与adjvex 数组;
注意:
更新lowcost 数组与adjvex 数组的条件: - 与顶点k 之间有连接
- 当前结点 j 没有加⼊入过最⼩小⽣生成树;
- 顶点 k 与 当前顶点 j 之间的权值 ⼩小于 顶点j 与其他顶点 k 之前的权值. 则更新. 简单说就是要⽐比较之前存储的值要小,则更新;
普里姆(Prim)算法执行过程
| 序号 | 数组变化前 | 数组变化前 |
|---|---|---|
| 第1次执行 |
 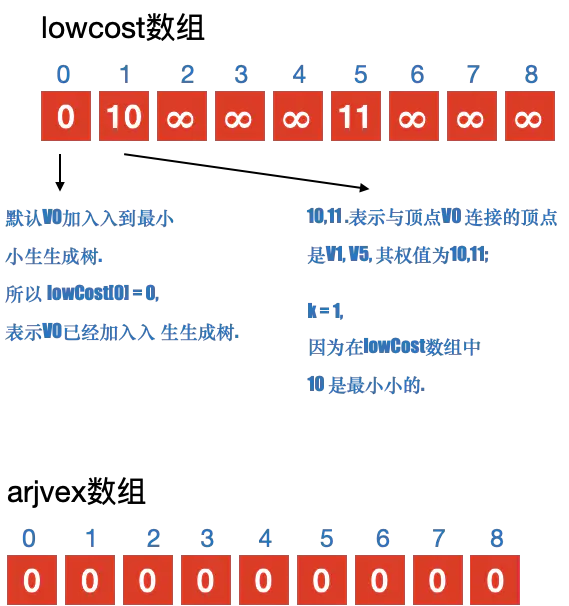 |
  |
| 第2次执行 |
  |
  |
| 第3次执行 |
  |
  |
| 第4次执行 |
  |
  |
| 第5次执行 |
  |
  |
| 第6次执行 |
  |
  |
| 第7次执行 |
  |
  |
| 8次执行 |
  |
  |
代码逻辑实现
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXEDGE 20 #define MAXVEX 20 #define INFINITYC 65535 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; /*9.1 创建邻接矩阵*/ void CreateMGraph(MGraph *G)/* 构件图 */ { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges=15; G->numVertexes=9; for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITYC; } } G->arc[0][1]=10; G->arc[0][5]=11; G->arc[1][2]=18; G->arc[1][8]=12; G->arc[1][6]=16; G->arc[2][8]=8; G->arc[2][3]=22; G->arc[3][8]=21; G->arc[3][6]=24; G->arc[3][7]=16; G->arc[3][4]=20; G->arc[4][7]=7; G->arc[4][5]=26; G->arc[5][6]=17; G->arc[6][7]=19; for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /* Prim算法生成最小生成树 */ void MiniSpanTree_Prim(MGraph G) { int min, i, j, k; int sum = 0; /* 保存相关顶点下标 */ int adjvex[MAXVEX]; /* 保存相关顶点间边的权值 */ int lowcost[MAXVEX]; /* 初始化第一个权值为0,即v0加入生成树 */ /* lowcost的值为0,在这里就是此下标的顶点已经加入生成树 */ lowcost[0] = 0; /* 初始化第一个顶点下标为0 */ adjvex[0] = 0; //1. 初始化 for(i = 1; i < G.numVertexes; i++) /* 循环除下标为0外的全部顶点 */ { lowcost[i] = G.arc[0][i]; /* 将v0顶点与之有边的权值存入数组 */ adjvex[i] = 0; /* 初始化都为v0的下标 */ } //2. 循环除了下标为0以外的全部顶点, 找到lowcost数组中最小的顶点k for(i = 1; i < G.numVertexes; i++) { /* 初始化最小权值为∞, */ /* 通常设置为不可能的大数字如32767、65535等 */ min = INFINITYC; j = 1;k = 0; while(j < G.numVertexes) /* 循环全部顶点 */ { /* 如果权值不为0且权值小于min */ if(lowcost[j]!=0 && lowcost[j] < min) { /* 则让当前权值成为最小值,更新min */ min = lowcost[j]; /* 将当前最小值的下标存入k */ k = j; } j++; } /* 打印当前顶点边中权值最小的边 */ printf("(V%d, V%d)=%d\n", adjvex[k], k ,G.arc[adjvex[k]][k]); sum+=G.arc[adjvex[k]][k]; /* 3.将当前顶点的权值设置为0,表示此顶点已经完成任务 */ lowcost[k] = 0; /* 循环所有顶点,找到与顶点k 相连接的顶点 1. 与顶点k 之间连接; 2. 该结点没有被加入到生成树; 3. 顶点k 与 顶点j 之间的权值 < 顶点j 与其他顶点的权值,则更新lowcost 数组; */ for(j = 1; j < G.numVertexes; j++) { /* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */ if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) { /* 将较小的权值存入lowcost相应位置 */ lowcost[j] = G.arc[k][j]; /* 将下标为k的顶点存入adjvex */ adjvex[j] = k; } } } printf("sum = %d\n",sum); } int main(void) { printf("Hello,最小生成树_Prim算法\n"); MGraph G; CreateMGraph(&G); MiniSpanTree_Prim(G); return 0; }
四:克鲁斯卡尔(Kruskal)算法
普里姆(Prim)算法是以某顶点为起点,逐步找各顶点上最小权值的边来构建最小生成树的。这就像是我们如果去参观某个展会,例如世博会,你从一个入口进去,然后找你所在位置周边的场馆中你最感兴趣的场馆观光,看完后再用同样的办法看下一个。可我们为什么不事先计划好,进园后直接到你最想去的场馆观看呢?事实上,去世博园的观众,绝大多数都是这样做的。
同样的思路,我们也可以直接就以边为目标去构建,因为权值是在边上,直接去找最小权值的边来构建生成树也是很自然的想法,只不过构建时要考虑是否会形成环路而已。此时我们就用到了图的存储结构中的边集数组结构。以下是edge边集数组结构的定义代码:
/* 对边集数组Edge结构的定义 */ typedef struct { int begin; int end; int weight; } Edge;
算法思路
- 将邻接矩阵 转化成 边表数组;
- 对边表数组根据权值按照从小到大的顺序排序;
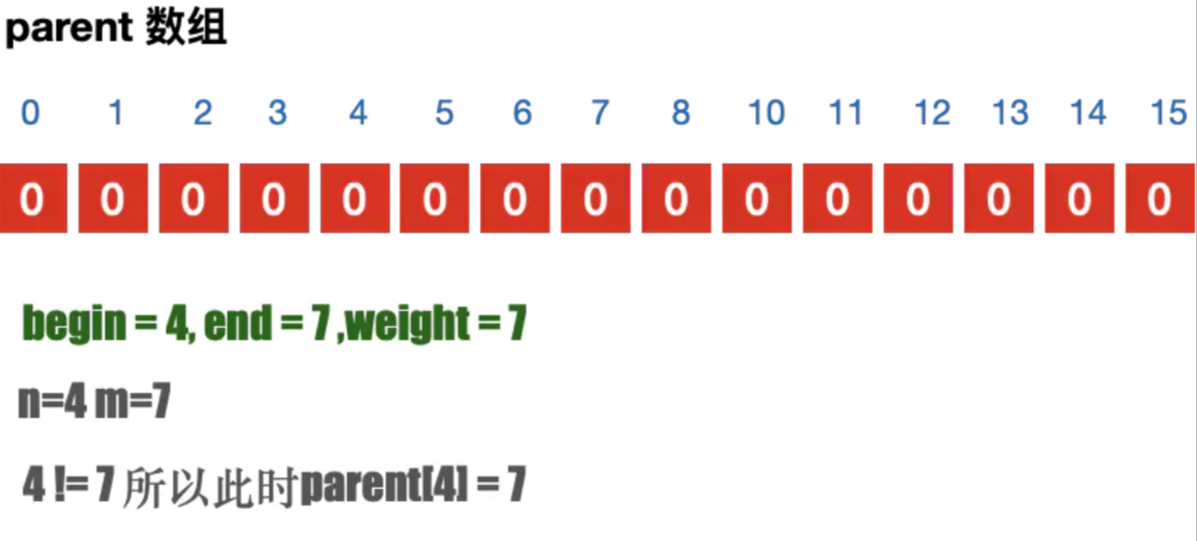
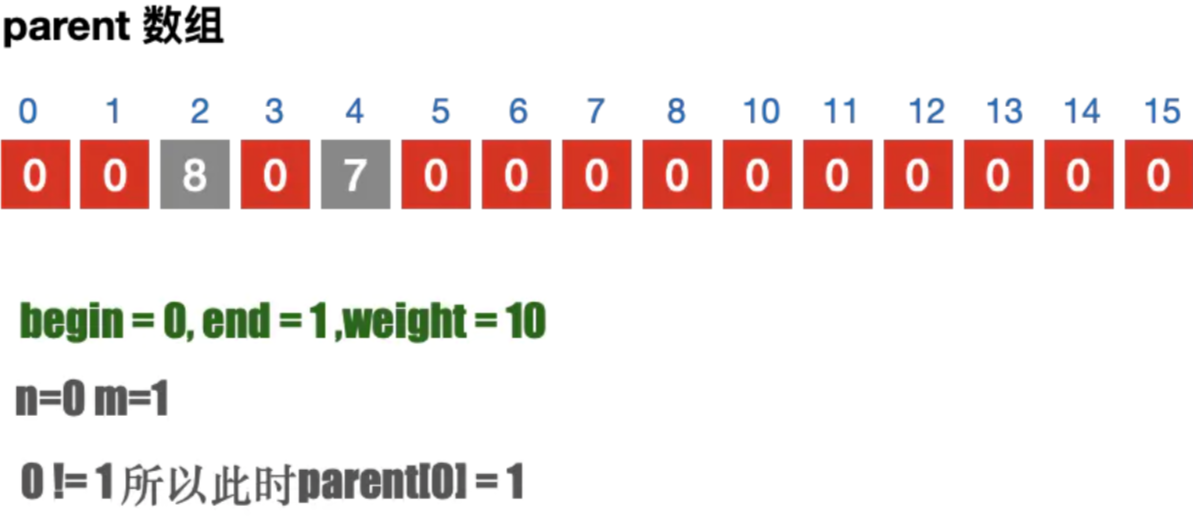
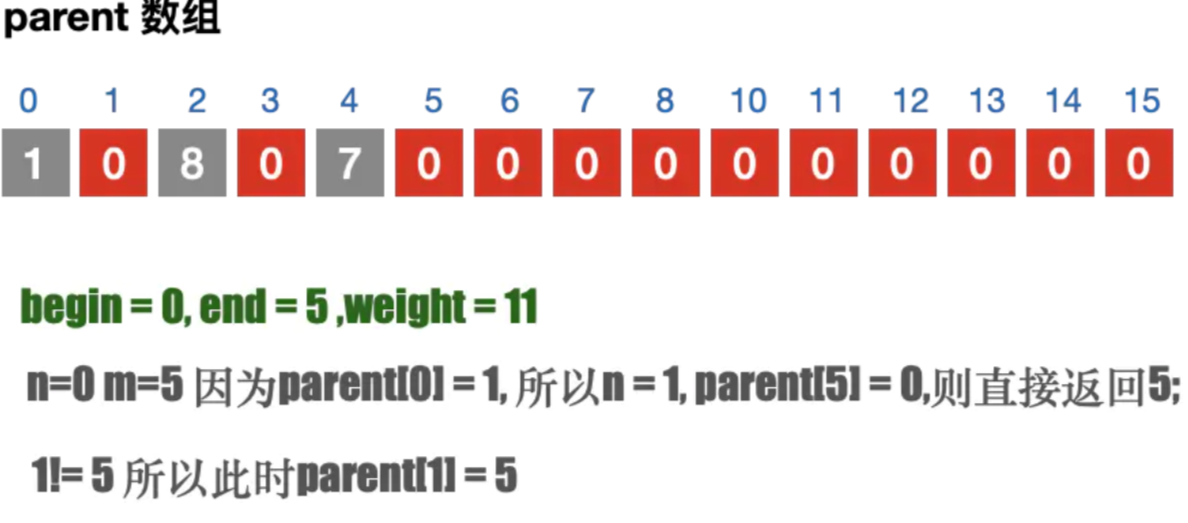
- 遍历所有的边, 通过parent 数组找到边的连接信息; 避免闭环问题;
- 如果不存在闭环问题,则加入到最⼩⽣成树中. 并且修改parent 数组
注意⚠️parent 数组的目的是为了判断当前的边是否会构成闭环
1、将邻接矩阵转化成边表数组,对边表数组根据权值按照从⼩小到⼤大的顺序排序;
规定小下标到大下标的方向
代码实现逻辑
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXEDGE 20 #define MAXVEX 20 #define INFINITYC 65535 typedef int Status; typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; /* 对边集数组Edge结构的定义 */ typedef struct { int begin; int end; int weight; }Edge ; /*9.1 创建邻接矩阵*/ void CreateMGraph(MGraph *G) { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges=15; G->numVertexes=9; for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITYC; } } G->arc[0][1]=10; G->arc[0][5]=11; G->arc[1][2]=18; G->arc[1][8]=12; G->arc[1][6]=16; G->arc[2][8]=8; G->arc[2][3]=22; G->arc[3][8]=21; G->arc[3][6]=24; G->arc[3][7]=16; G->arc[3][4]=20; G->arc[4][7]=7; G->arc[4][5]=26; G->arc[5][6]=17; G->arc[6][7]=19; for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /* 交换权值以及头和尾 */ void Swapn(Edge *edges,int i, int j) { int tempValue; //交换edges[i].begin 和 edges[j].begin 的值 tempValue = edges[i].begin; edges[i].begin = edges[j].begin; edges[j].begin = tempValue; //交换edges[i].end 和 edges[j].end 的值 tempValue = edges[i].end; edges[i].end = edges[j].end; edges[j].end = tempValue; //交换edges[i].weight 和 edges[j].weight 的值 tempValue = edges[i].weight; edges[i].weight = edges[j].weight; edges[j].weight = tempValue; } /* 对权值进行排序 */ void sort(Edge edges[],MGraph *G) { //对权值进行排序(从小到大) int i, j; for ( i = 0; i < G->numEdges; i++) { for ( j = i + 1; j < G->numEdges; j++) { if (edges[i].weight > edges[j].weight) { Swapn(edges, i, j); } } } printf("边集数组根据权值排序之后的为:\n"); for (i = 0; i < G->numEdges; i++) { printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight); } } /* 查找连线顶点的尾部下标 */ //根据顶点f以及parent 数组,可以找到当前顶点的尾部下标; 帮助我们判断2点之间是否存在闭环问题; int Find(int *parent, int f) { while ( parent[f] > 0) { f = parent[f]; } return f; } /* 生成最小生成树 */ void MiniSpanTree_Kruskal(MGraph G) { int i, j, n, m; int sum = 0; int k = 0; /* 定义一数组用来判断边与边是否形成环路 用来记录顶点间的连接关系. 通过它来防止最小生成树产生闭环;*/ int parent[MAXVEX]; /* 定义边集数组,edge的结构为begin,end,weight,均为整型 */ Edge edges[MAXEDGE]; /*1. 用来构建边集数组*/ for ( i = 0; i < G.numVertexes-1; i++) { for (j = i + 1; j < G.numVertexes; j++) { //如果当前路径权值 != ∞ if (G.arc[i][j]<INFINITYC) { //将路径对应的begin,end,weight 存储到edges 边集数组中. edges[k].begin = i; edges[k].end = j; edges[k].weight = G.arc[i][j]; //边集数组计算器k++; k++; } } } //2. 对边集数组排序 sort(edges, &G); //3.初始化parent 数组为0. 9个顶点; // for (i = 0; i < G.numVertexes; i++) for (i = 0; i < MAXVEX; i++) parent[i] = 0; //4. 计算最小生成树 printf("打印最小生成树:\n"); /* 循环每一条边 G.numEdges 有15条边*/ for (i = 0; i < G.numEdges; i++) { //获取begin,end 在parent 数组中的信息; //如果n = m ,将begin 和 end 连接,就会产生闭合的环. n = Find(parent,edges[i].begin); m = Find(parent,edges[i].end); //printf("n = %d,m = %d\n",n,m); /* 假如n与m不等,说明此边没有与现有的生成树形成环路 */ if (n != m) { /* 将此边的结尾顶点放入下标为起点的parent中。 */ /* 表示此顶点已经在生成树集合中 */ parent[n] = m; /*打印最小生成树路径*/ printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight); sum += edges[i].weight; } } printf("sum = %d\n",sum); } int main(int argc, const char * argv[]) { printf("Hello,最小生成树_Kruskal算法\n"); MGraph G; CreateMGraph(&G); MiniSpanTree_Kruskal(G); return 0; }
引用
1:图的应用(最小生成树Prim算法与Kruskal算法实现与分析)
Kruskal算法执行过程
| 最小生成树循环次数 | 数组变化前 | 数组变化前 |
|---|---|---|
| 第1次执行 |
 |
  |
| 第2次执行 |
 |

|
| 第3次执行 |
  |

 |
| 第4次执行 |
 |

 |
| 第5次执行 |
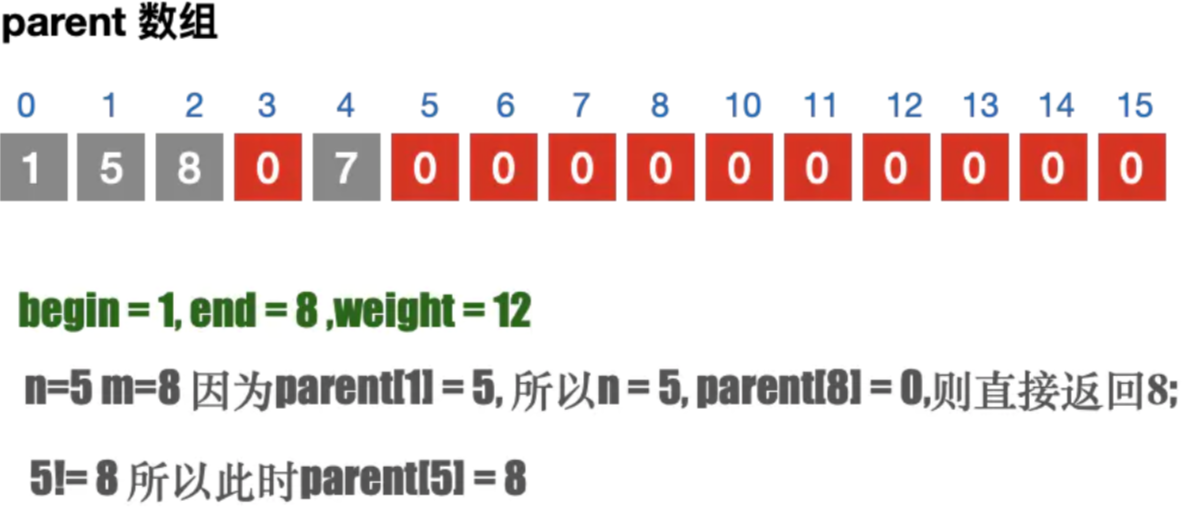 |

 |
| 第6次执行 |
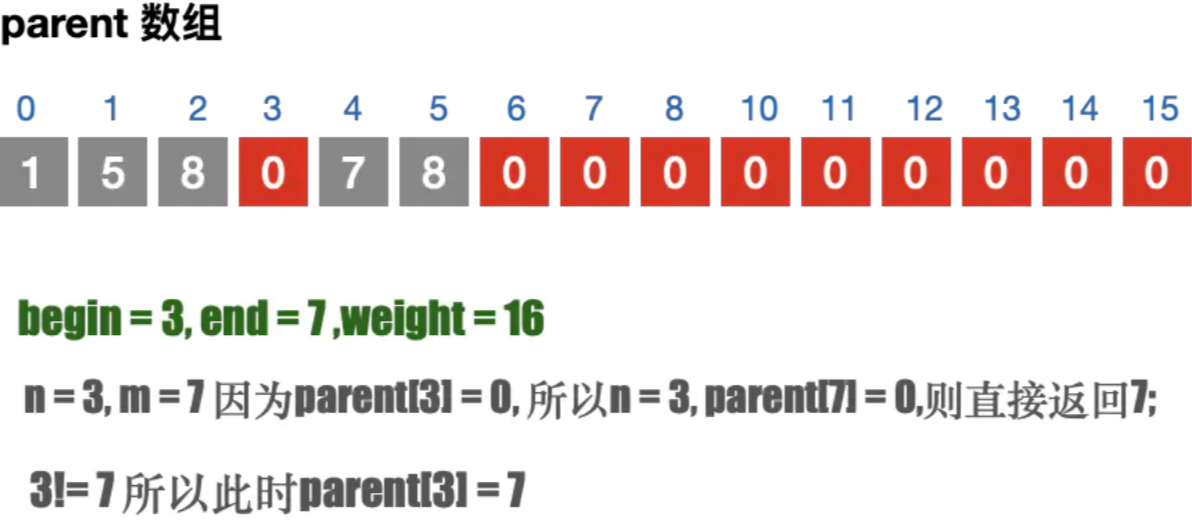 |

 |
| 第7次执行 |
 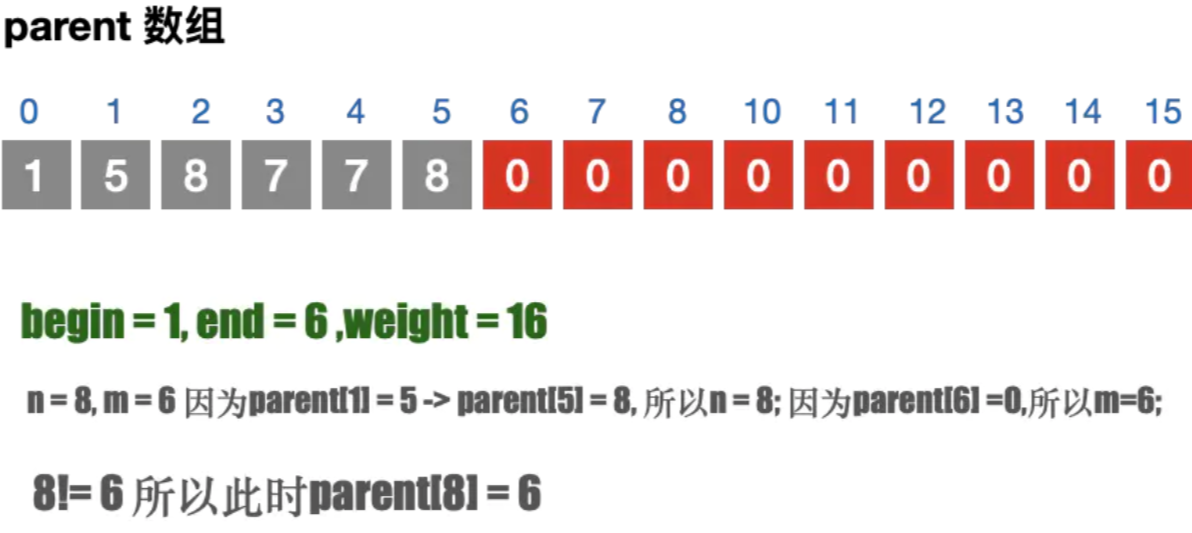 |

 |
| 分析 |
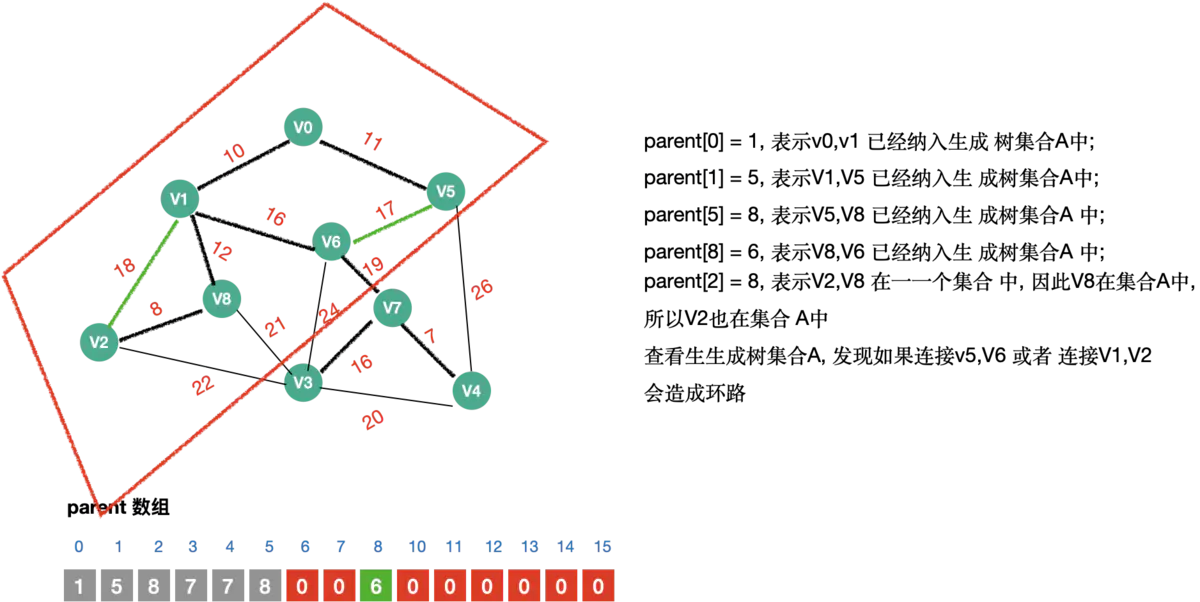  |
|
| 第8次执行 |
 |

 |
| 第9次执行 |
 |

 |
| 第10次执行 |
  |

 |
| 第11次执行 |
 |

 |
| 第12次执行 |
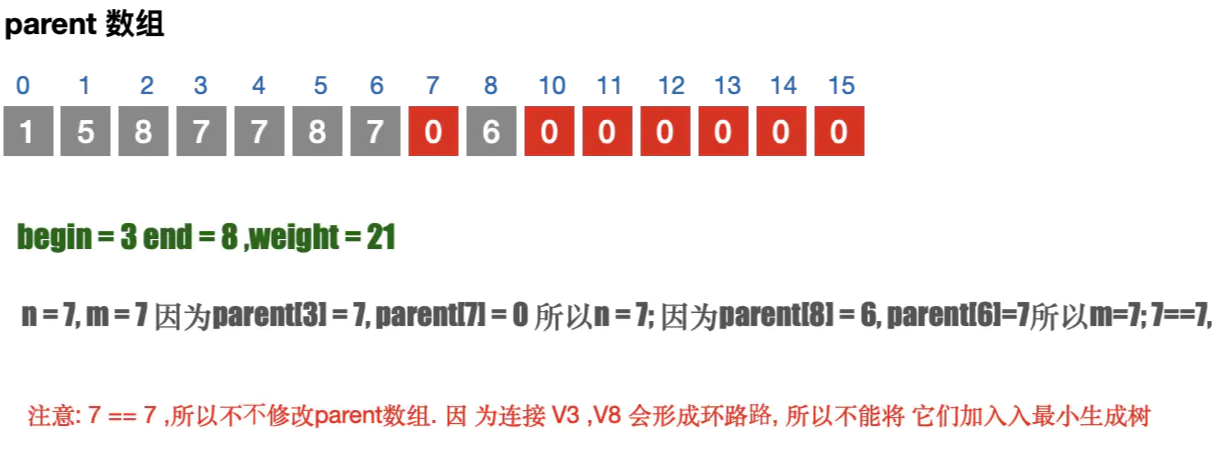 |

 |
| 第13次执行 |
  |
 
|
| 第14次执行 |
 |

 |
| 第15次执行 |
 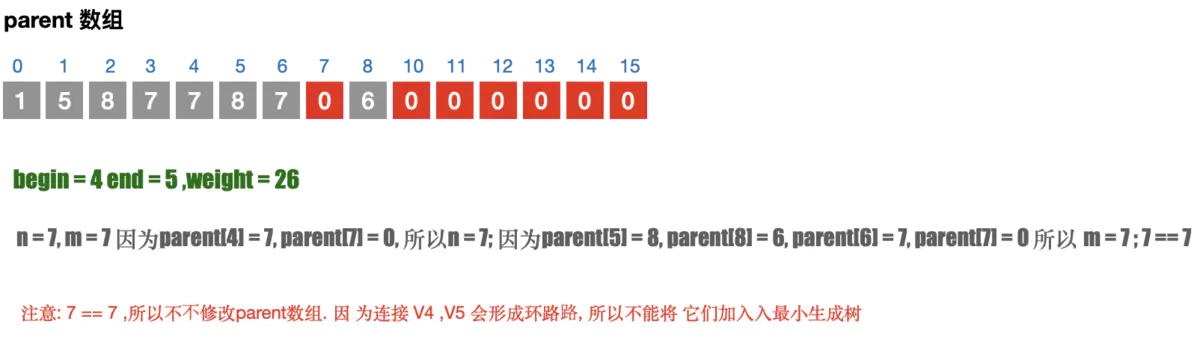 |
 
|



