12*:图结构初探:(邻接矩阵顺序存储、邻接表链式存储)(邻接矩阵和邻接表以及深度与广度优先遍历)
问题
目录
1:图
2:邻接矩阵顺序存储、
3:邻接表链式存储
4:邻接矩阵和邻接表、及深度与广度优先遍历
预备
正文
一:图
1:图的简介
图(Graph)结构是一种非线性的数据结构,图在实际生活中有很多例子,比如交通运输网,地铁网络,社交网络,计算机中的状态执行(自动机)等等都可以抽象成图结构。图结构比树结构复杂的非线性结构
2:图的构成
图(Graph) 是由顶点的有穷⾮非空集合 和 顶点之间边的集合组成. 通常表示为: G(V,E). 其中,G表示⼀一个图, V(vertex顶点)是图G中的顶点集合,E(edge边)是图G中边的集合.
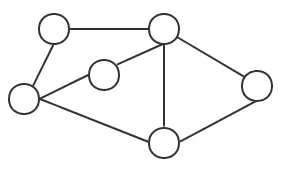
图结构中顶点集合V(G)不能为空,必须包含一个顶点,而图结构边集合可以为空,表示没有边.
3:图的基本概念
1.无向图(undirected graph)
如果一个图结构中,所有的边都没有方向性,那么这种图便称为无向图。典型的无向图,如图二所示。由于无向图中的边没有方向性,这样我们在表示边的时候对两个顶点的顺序没有要求
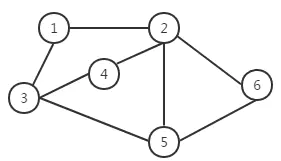
2.有向图(undirected graph)
一个图结构中,边是有方向性的,那么这种图就称为有向图,如图三所示。由于图的边有方向性,我们在表示边的时候对两个顶点的顺序就有要求
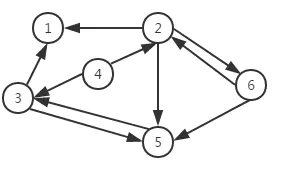
注意:
无向图也可以理解成一个特殊的有向图,就是边互相指向对方节点,A指向B,B又指向A
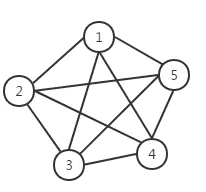
3.无向完全图
如果在一个无向图中, 每两个顶点之间都存在条边,那么这种图结构称为无向完全图。
4.有向完全图
如果在一个有向图中,每两个顶点之间都存在方向相反的两条边,那么这种图结构称为有向完全图

5.顶点的度
连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图,一个顶点V的度比较简单,其是连接该顶点的边的数量,记为D(V)。
对于有向图要稍复杂些,根据连接顶点V的边的方向性,一个顶点的度有入度和出度之分。
入度是以该顶点为端点的入边数量, 记为ID(V)。
出度是以该顶点为端点的出边数量, 记为OD(V)。
这样,有向图中,一个顶点V的总度便是入度和出度之和,即D(V) = ID(V) + OD(V)。
6.无权图和带权图
无权图:
顶点与顶点之间没有权重
带权图:
带权图表示边有一定的权重. 数学的加权平均数的概念
这里的权重可以是任意你希望表示的数据: 比如距离或者花费的时间或者票价.
4:图的表示
怎么在程序中表示图呢?
我们知道一个图包含很多顶点, 另外包含顶点和顶点之间的连线(边), 这两个都是非常重要的图信息, 因此都需要在程序中体现出来.
[数据结构与算法设计] 将左边图存储到计算机中.请设 计⼀一个数据结构并将其合理理存储起来. #快手⾯试真题#
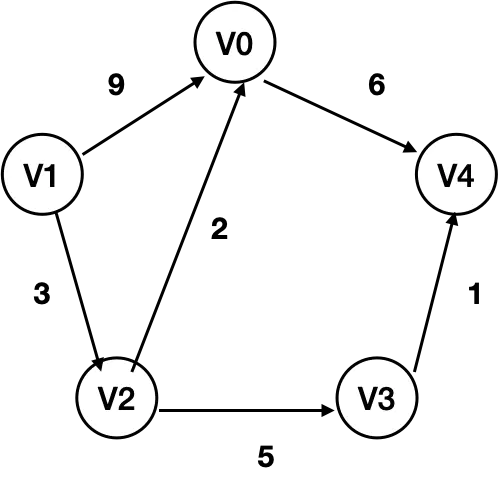
5:顶点表示:
• 顶点的表示相对简单, 我们先讨论顶点的表示.
• 上面的顶点, 我们抽象成了1 2 3 4 5, 也可以抽象成A B C D E. 在后面的案例中
• 那么这些A B C D E我们可以使用一个数组来存储起来(存储所有的顶点)
• 当然, A, B, C, D E有可能还表示其他含义的数据(比如村庄的名字), 这个时候, 可以另外创建一个数组, 用于存储对应的其他数据.
• 那么边怎么表示呢?
• 因为边是两个顶点之间的关系, 所以表示起来会稍微麻烦一些.
• 下面, 我们具体讨论一下变常见的表示方式.
二:邻接矩阵顺序存储
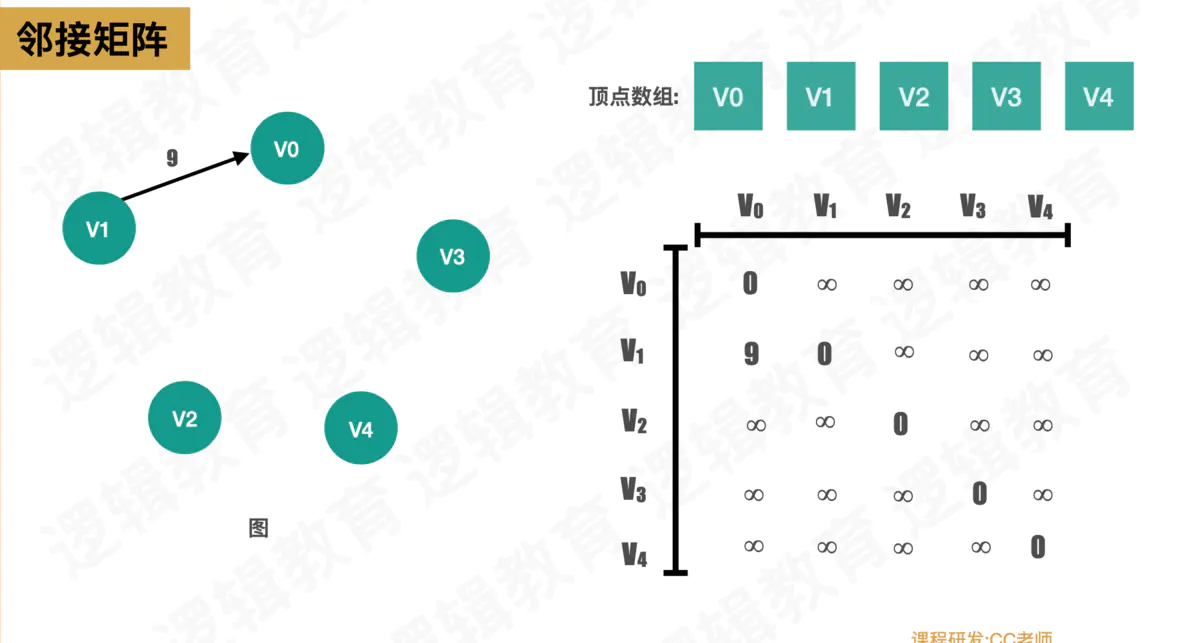
• 一种比较常见的表示图的方式: 邻接矩阵.
• 邻接矩阵让每个节点和一个整数向关联, 该整数作为数组的下标值.
• 我们用一个二维数组来表示顶点之间的连接.
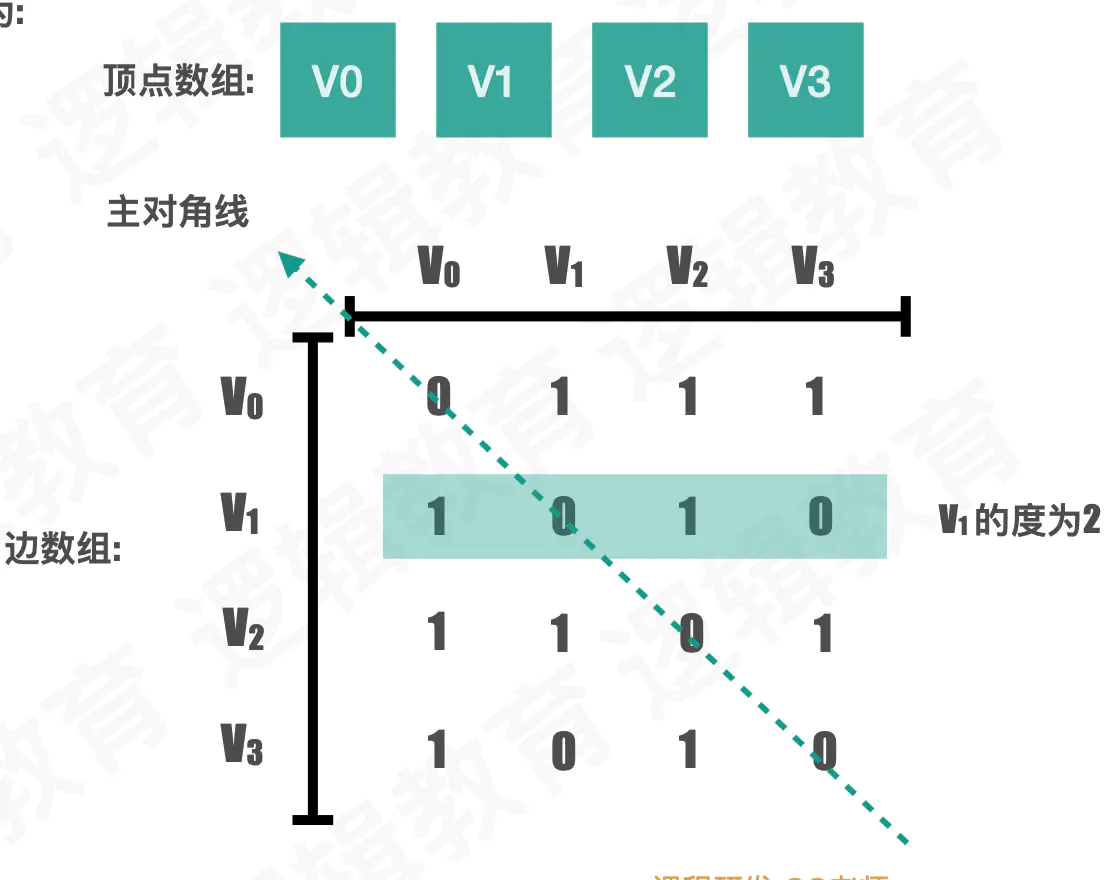
图片解析:
在二维数组中, 0表示没有连线, 1表示有连线.
通过二维数组, 我们可以很快的找到一个顶点和哪些顶点有连线.(比如v0顶点, 只需要遍历第一行即可)
另外, 也就是顶点到自己的连线, 通常使用0表示.
邻接矩阵的问题:
如果是一个无向图, 邻接矩阵展示出来的二维数组, 其实是一个对称图.
也就是V0->V4 是1的时候, 对称的位置 V4->V0 一定也是1.
那么这种情况下会造成空间的浪费, 你有没有办法可以优化呢?
代码实现
- 确定顶点数/边数
- 读取顶点信息
- 初始化邻接矩阵
- 读⼊入边信息
- 循环打印
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXVEX 100 /* 最大顶点数,应由用户定义 */ #define INFINITYC 0 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numNodes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; void CreateMGraph(MGraph *G){ int i,j,k,w; printf("输入顶点数和边数:\n"); //1. 输入顶点数/边数 scanf("%d,%d",&G->numNodes,&G->numEdges); printf("顶点数:%d,边数:%d\n",G->numNodes,G->numEdges); //2.输入顶点信息/顶点表 for(i = 0; i<= G->numNodes;i++) scanf("%c",&G->vexs[i]); //3.初始化邻接矩阵 for(i = 0; i < G->numNodes;i++) for(j = 0; j < G->numNodes;j++) G->arc[i][j] = INFINITYC; //4.输入边表信息 for(k = 0; k < G->numEdges;k++){ printf("输入边(vi,vj)上的下标i,下标j,权w\n"); scanf("%d,%d,%d",&i,&j,&w); G->arc[i][j] = w; //如果无向图,矩阵对称; G->arc[j][i] = G->arc[i][j]; } /*5.打印邻接矩阵*/ for (int i = 0; i < G->numNodes; i++) { printf("\n"); for (int j = 0; j < G->numNodes; j++) { printf("%d ",G->arc[i][j]); } } printf("\n"); } int main(void) { printf("邻接矩阵实现图的存储\n"); /*图的存储-邻接矩阵*/ MGraph G; CreateMGraph(&G); return 0; }
三:邻接表链式存储
无向表链式结构
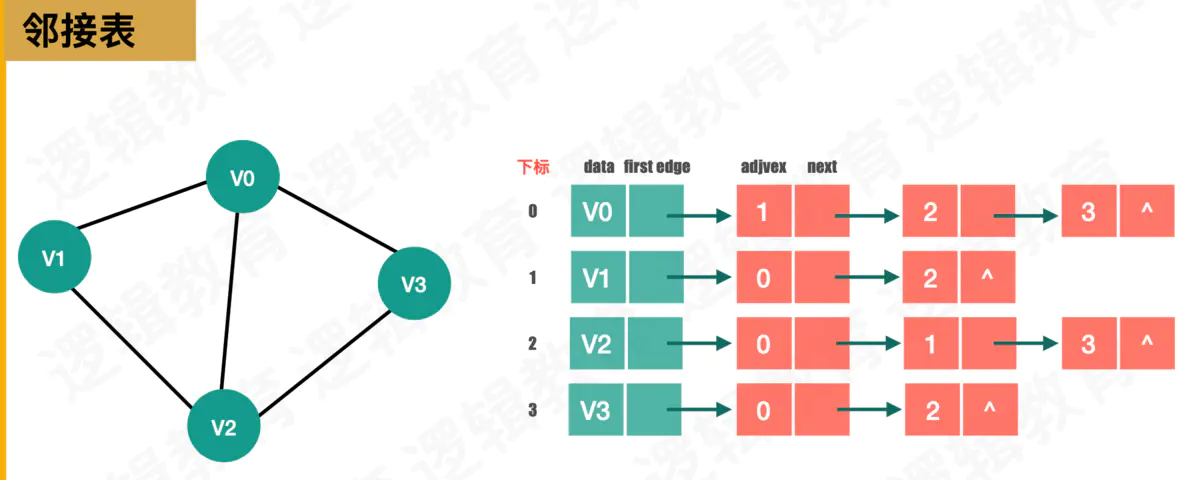
右向表链式结构
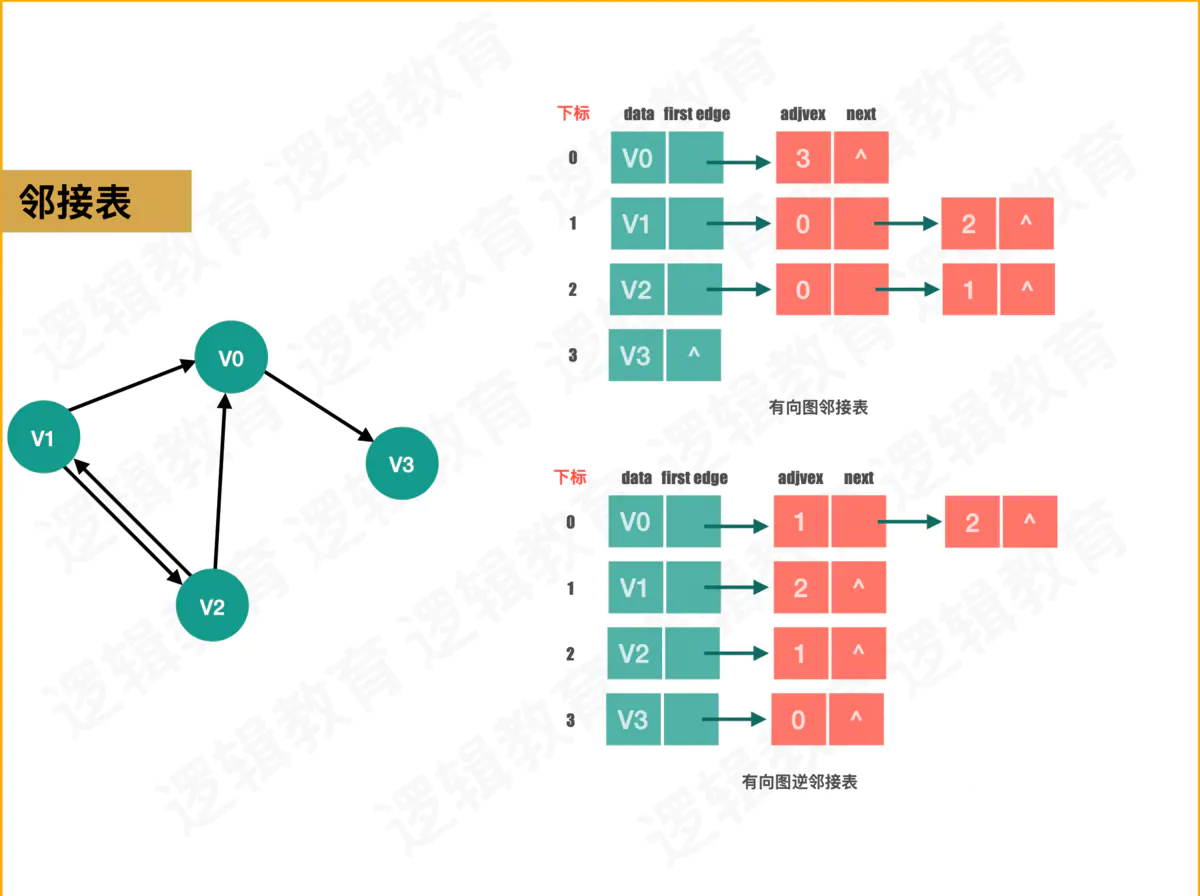
有向表有权链式结构
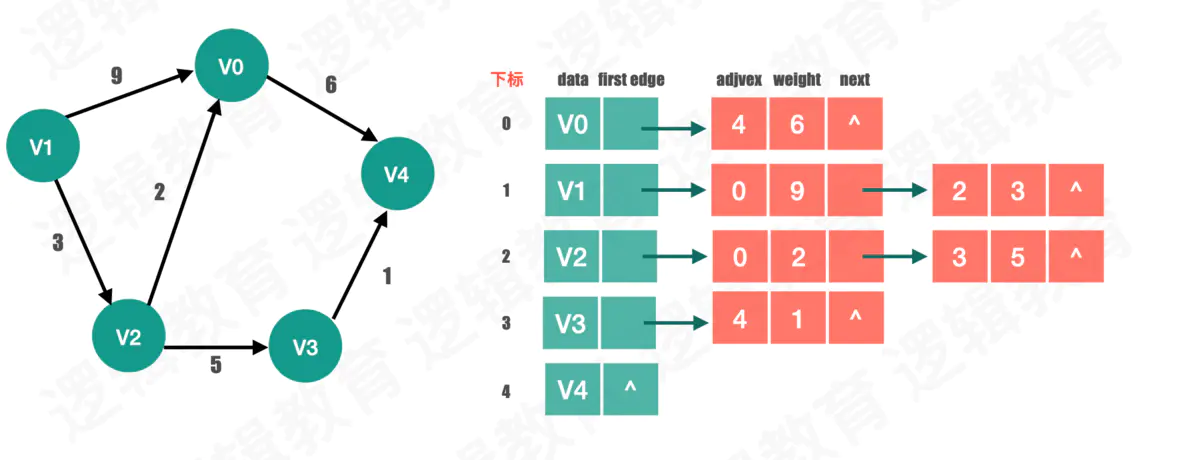
邻接表存储的存储代码实现思路
#include "stdio.h"
#include "stdlib.h" #include "math.h" #include "time.h" #define M 100 #define true 1 #define false 0 typedef char Element; typedef int BOOL; //邻接表的节点 typedef struct Node{ int adj_vex_index; //弧头的下标,也就是被指向的下标 Element data; //权重值 struct Node * next; //边指针 }EdgeNode; //顶点节点表 typedef struct vNode{ Element data; //顶点的权值 EdgeNode * firstedge; //顶点下一个是谁? }VertexNode, Adjlist[M]; //总图的一些信息 typedef struct Graph{ Adjlist adjlist; //顶点表 int arc_num; //边的个数 int node_num; //节点个数 BOOL is_directed; //是不是有向图 }Graph, *GraphLink; void creatGraph(GraphLink *g){ int i,j,k; EdgeNode *p; //1. 顶点,边,是否有向 printf("输入顶点数目,边数和有向?:\n"); scanf("%d %d %d", &(*g)->node_num, &(*g)->arc_num, &(*g)->is_directed); //2.顶点表 printf("输入顶点信息:\n"); for (i = 0; i < (*g)->node_num; i++) { getchar(); scanf("%c", &(*g)->adjlist[i].data); (*g)->adjlist[i].firstedge = NULL; } //3. printf("输入边信息:\n"); for (k = 0; k < (*g)->arc_num; k++){ getchar(); scanf("%d %d", &i, &j); //①新建一个节点 p = (EdgeNode *)malloc(sizeof(EdgeNode)); //②弧头的下标 p->adj_vex_index = j; //③头插法插进去,插的时候要找到弧尾,那就是顶点数组的下标i p->next = (*g)->adjlist[i].firstedge; //④将顶点数组[i].firstedge 设置为p (*g)->adjlist[i].firstedge = p; //j->i if(!(*g)->is_directed) { // j -----> i //①新建一个节点 p = (EdgeNode *)malloc(sizeof(EdgeNode)); //②弧头的下标i p->adj_vex_index = i; //③头插法插进去,插的时候要找到弧尾,那就是顶点数组的下标i p->next = (*g)->adjlist[j].firstedge; //④将顶点数组[i].firstedge 设置为p (*g)->adjlist[j].firstedge = p; } } } void putGraph(GraphLink g){ int i; printf("邻接表中存储信息:\n"); //遍历一遍顶点坐标,每个再进去走一次 for (i = 0; i < g->node_num; i++) { EdgeNode * p = g->adjlist[i].firstedge; while (p) { printf("%c->%c ", g->adjlist[i].data, g->adjlist[p->adj_vex_index].data); p = p->next; } printf("\n"); } } int main(int argc, const char * argv[]) { // insert code here... printf("邻接表实现图的存储\n"); /* 邻接表实现图的存储 输入顶点数目,边数和有向?: 4 5 0 输入顶点信息: 0 1 2 3 输入边信息: 0 1 0 2 0 3 2 1 2 3 邻接表中存储信息: 0->3 0->2 0->1 1->2 1->0 2->3 2->1 2->0 3->2 3->0 */ /* 邻接表实现图的存储 输入顶点数目,边数和有向?: 4 5 1 输入顶点信息: 0 1 2 3 输入边信息: 1 0 1 2 2 1 2 0 0 3 邻接表中存储信息: 0->3 1->2 1->0 2->0 2->1 */ GraphLink g = (Graph *)malloc(sizeof(Graph)); creatGraph(&g); putGraph(g); return 0; }
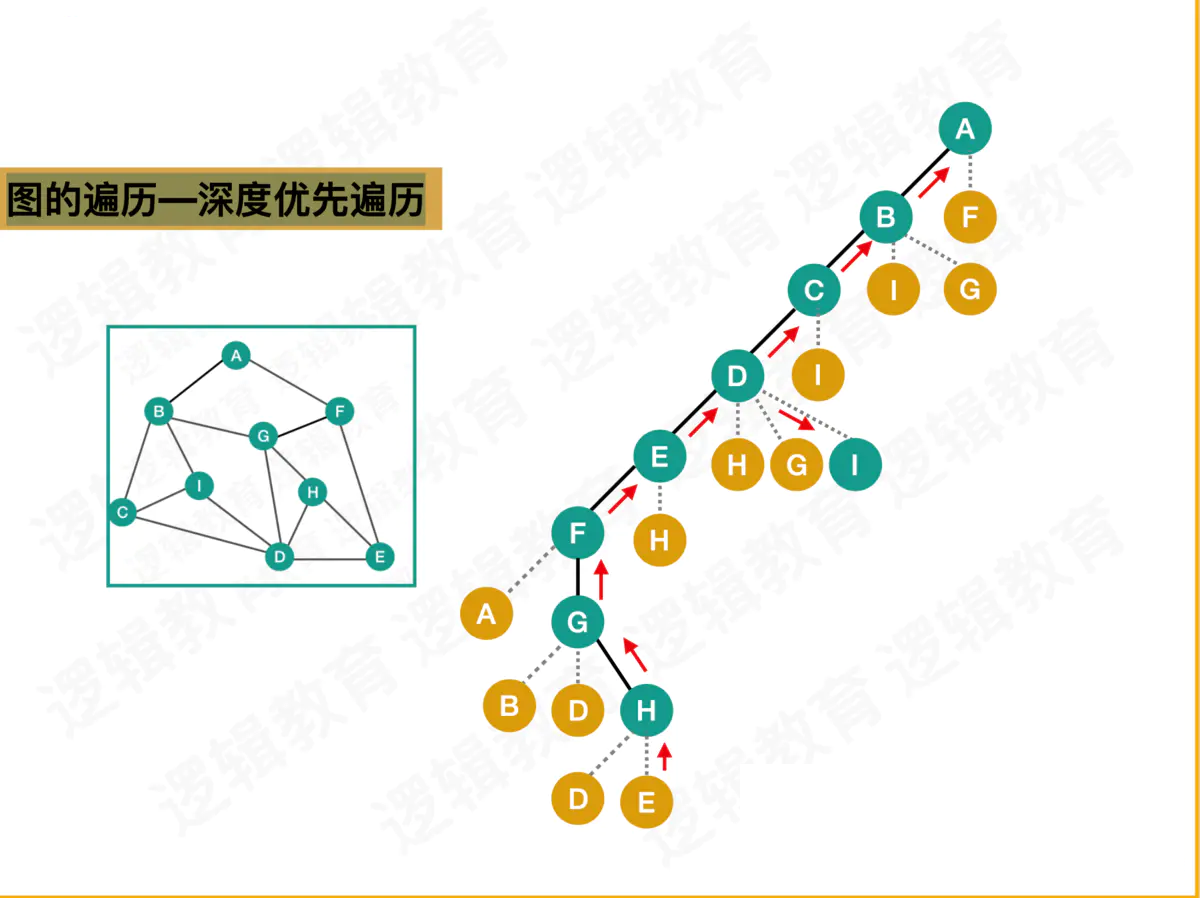
四:图的遍历
图的遍历—深度优先遍历
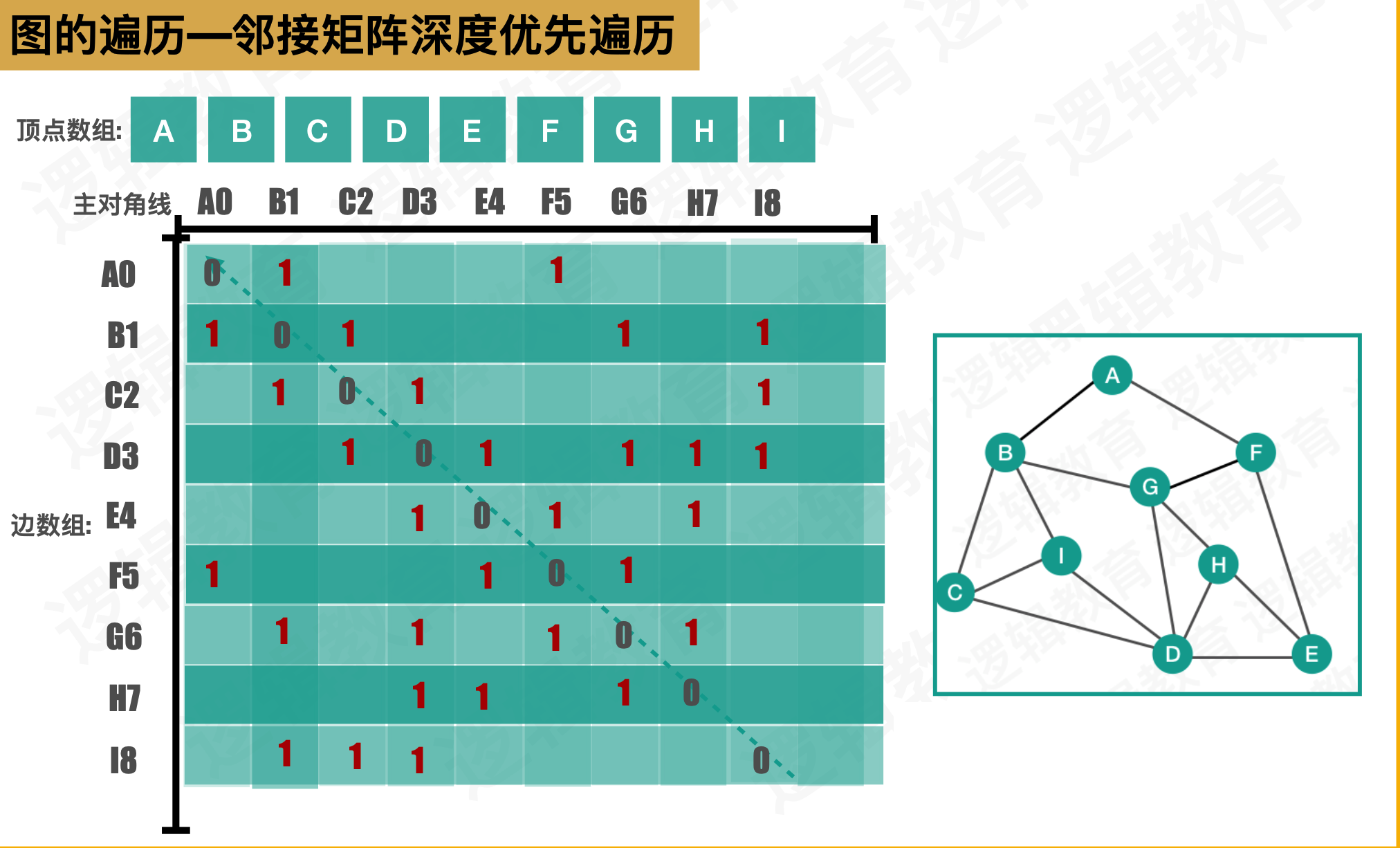
1:图的遍历—邻接矩阵深度优先遍历代码实现思路路
- 将图的顶点和边信息输⼊入到图结构中;
- 创建⼀一个visited 数组,⽤用来标识顶点是否已经被遍历过.
- 初始化visited 数组,将数组中元素置为FALSE
- 选择顶点开始遍历.(注意⾮非连通图的情况)
- 进⼊递归; 打印i 对应的顶点信息. 并将该顶点标识为已遍历.
- 循环遍历边表,判断当前arc[i][j] 是否等于1,并且当前该顶点没有被遍历过,则继续递归 DFS;
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ #define MAXSIZE 9 /* 存储空间初始分配量 */ #define MAXEDGE 15 #define MAXVEX 9 #define INFINITYC 65535 typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numVertexes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; /*4.1 构建一个邻接矩阵*/ void CreateMGraph(MGraph *G) { int i, j; //1. 确定图的顶点数以及边数 G->numEdges=15; G->numVertexes=9; /*2.读入顶点信息,建立顶点表 */ G->vexs[0]='A'; G->vexs[1]='B'; G->vexs[2]='C'; G->vexs[3]='D'; G->vexs[4]='E'; G->vexs[5]='F'; G->vexs[6]='G'; G->vexs[7]='H'; G->vexs[8]='I'; /*3. 初始化图中的边表*/ for (i = 0; i < G->numVertexes; i++) { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } } /*4.将图中的连接信息输入到边表中*/ G->arc[0][1]=1; G->arc[0][5]=1; G->arc[1][2]=1; G->arc[1][8]=1; G->arc[1][6]=1; G->arc[2][3]=1; G->arc[2][8]=1; G->arc[3][4]=1; G->arc[3][7]=1; G->arc[3][6]=1; G->arc[3][8]=1; G->arc[4][5]=1; G->arc[4][7]=1; G->arc[5][6]=1; G->arc[6][7]=1; /*5.无向图是对称矩阵.构成对称*/ for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /*4.2 DFS遍历*/ Boolean visited[MAXVEX]; /* 访问标志的数组 */ //1. 标识顶点是否被标记过; //2. 选择从某一个顶点开始(注意:非连通图的情况) //3. 进入递归,打印i点信息,标识; 边表 //4. [i][j] 是否等于1,没有变遍历过visted void DFS(MGraph G,int i){ //1. visited[i] = TRUE; printf("%c",G.vexs[i]); //2.0~numVertexes for(int j = 0; j < G.numVertexes;j++){ if(G.arc[i][j] == 1 && !visited[j]) DFS(G, j); } } void DFSTravese(MGraph G){ //1.初始化 for(int i=0;i<G.numVertexes;i++){ visited[i] = FALSE; } //2.某一个顶点 for(int i = 0;i<G.numVertexes;i++){ if(!visited[i]){ DFS(G, i); } } } int main(int argc, const char * argv[]) { // insert code here... printf("邻接矩阵的深度优先遍历!\n"); MGraph G; CreateMGraph(&G); DFSTravese(G); printf("\n"); return 0; }
深度优先遍历结果:
AFGHEDICB
2:图的遍历—邻接表对图的遍历处理
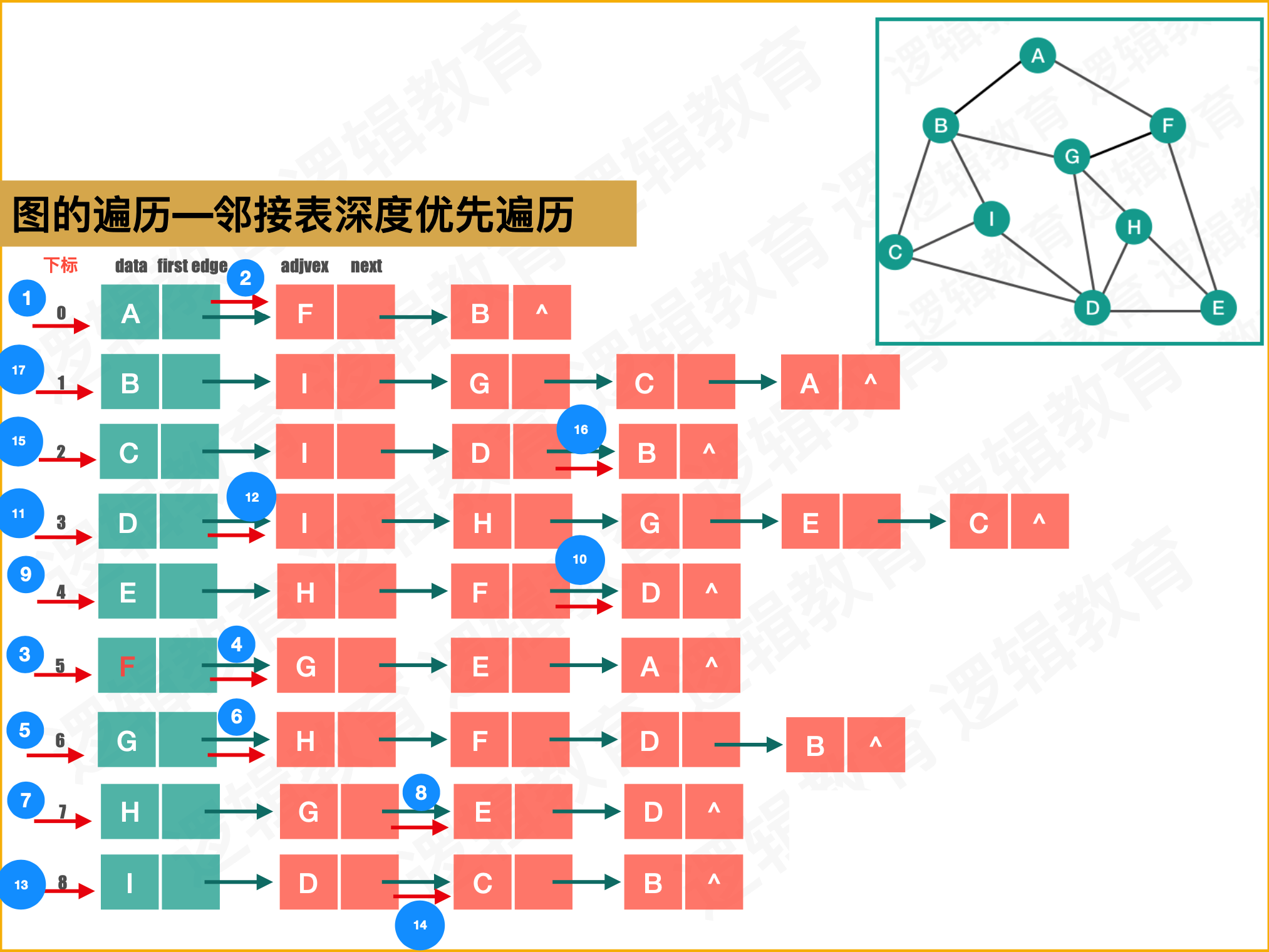
图的遍历—邻接表深度优先遍历代码实现思路路
- 利利⽤用邻接矩阵将信息存储到邻接表中
- 创建⼀一个visited 数组,⽤用来标识顶点是否已经被遍历过.
- 初始化visited 数组,将数组中元素置为FALSE
- 选择顶点开始遍历.(注意⾮非连通图的情况)
- 进⼊入递归; 打印i 对应的顶点信息. 并将该顶点标识为已遍历.
- 循环遍历边表,判断当前顶点 是否等于1,并且当前该顶点没有被遍历过,则继续递归 DFS;
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 9 /* 存储空间初始分配量 */ #define MAXEDGE 15 #define MAXVEX 9 #define INFINITYC 65535 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ /* 邻接矩阵结构 */ typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numVertexes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; /* 邻接表结构****************** */ typedef struct EdgeNode /* 边表结点 */ { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ int weight; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; typedef struct VertexNode /* 顶点表结点 */ { int in; /* 顶点入度 */ char data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; typedef struct { AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */ }graphAdjList,*GraphAdjList; /*4.1 构建一个邻接矩阵*/ void CreateMGraph(MGraph *G) { int i, j; //1. 确定图的顶点数以及边数 G->numEdges=15; G->numVertexes=9; /*2.读入顶点信息,建立顶点表 */ G->vexs[0]='A'; G->vexs[1]='B'; G->vexs[2]='C'; G->vexs[3]='D'; G->vexs[4]='E'; G->vexs[5]='F'; G->vexs[6]='G'; G->vexs[7]='H'; G->vexs[8]='I'; /*3. 初始化图中的边表*/ for (i = 0; i < G->numVertexes; i++) { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } } /*4.将图中的连接信息输入到边表中*/ G->arc[0][1]=1; G->arc[0][5]=1; G->arc[1][2]=1; G->arc[1][8]=1; G->arc[1][6]=1; G->arc[2][3]=1; G->arc[2][8]=1; G->arc[3][4]=1; G->arc[3][7]=1; G->arc[3][6]=1; G->arc[3][8]=1; G->arc[4][5]=1; G->arc[4][7]=1; G->arc[5][6]=1; G->arc[6][7]=1; /*5.无向图是对称矩阵.构成对称*/ for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /*4.2 利用邻接矩阵构建邻接表*/ void CreateALGraph(MGraph G,GraphAdjList *GL){ //1.创建邻接表,并且设计邻接表的顶点数以及弧数 *GL = (GraphAdjList)malloc(sizeof(graphAdjList)); (*GL)->numVertexes = G.numVertexes; (*GL)->numEdges = G.numEdges; //2. 从邻接矩阵中将顶点信息输入 for (int i = 0; i < G.numVertexes; i++) { //顶点入度为0 (*GL)->adjList[i].in = 0; //顶点信息 (*GL)->adjList[i].data = G.vexs[i]; //顶点边表置空 (*GL)->adjList[i].firstedge = NULL; } //3. 建立边表 EdgeNode *e; for (int i = 0; i < G.numVertexes; i++) { for (int j = 0; j < G.numVertexes; j++) { if (G.arc[i][j] == 1) { //创建边表中的邻近结点 i->j e = (EdgeNode *)malloc(sizeof(EdgeNode)); //邻接序号为j e->adjvex = j; //将当前结点的指向adjList[i]的顶点边表上 e->next = (*GL)->adjList[i].firstedge; (*GL)->adjList[i].firstedge = e; //顶点j 上的入度++; (*GL)->adjList[j].in++; // //创建边表中的邻近结点 j->i // e = (EdgeNode *)malloc(sizeof(EdgeNode)); // //邻接序号为j // e->adjvex = i; // //将当前结点的指向adjList[i]的顶点边表上 // e->next = (*GL)->adjList[j].firstedge; // (*GL)->adjList[j].firstedge = e; // //顶点j 上的入度++; // (*GL)->adjList[i].in++; } } } } Boolean visited[MAXSIZE]; /* 访问标志的数组 */ /* 邻接表的深度优先递归算法 */ void DFS(GraphAdjList GL, int i) { EdgeNode *p; visited[i] = TRUE; //2.打印顶点 A printf("%c ",GL->adjList[i].data); p = GL->adjList[i].firstedge; //3. while (p) { if(!visited[p->adjvex]) DFS(GL,p->adjvex); p = p->next; } } /* 邻接表的深度遍历操作 */ void DFSTraverse(GraphAdjList GL) { //1. 将访问记录数组默认置为FALSE for (int i = 0; i < GL->numVertexes; i++) { /*初始化所有顶点状态都是未访问过的状态*/ visited[i] = FALSE; } //2. 选择一个顶点开始DFS遍历. 例如A for(int i = 0; i < GL->numVertexes; i++) //对未访问过的顶点调用DFS, 若是连通图则只会执行一次. if(!visited[i]) DFS(GL, i); } int main(int argc, const char * argv[]) { // insert code here... printf("邻接表的深度优先遍历!\n"); MGraph G; GraphAdjList GL; CreateMGraph(&G); CreateALGraph(G,&GL); DFSTraverse(GL); printf("\n"); return 0; }
3:图的遍历—广度优先遍历
1、把根节点放到队列列的末尾。
2、每次从队列列的头部取出⼀一个元素,查看这个元素所有的下⼀一级元素,把它们放到队
列列的末尾。并把这个元素记为它下⼀一级元素的前驱。
3、找到所要找的元素时结束程序。
4、如果遍历整个树还没有找到,结束程序.
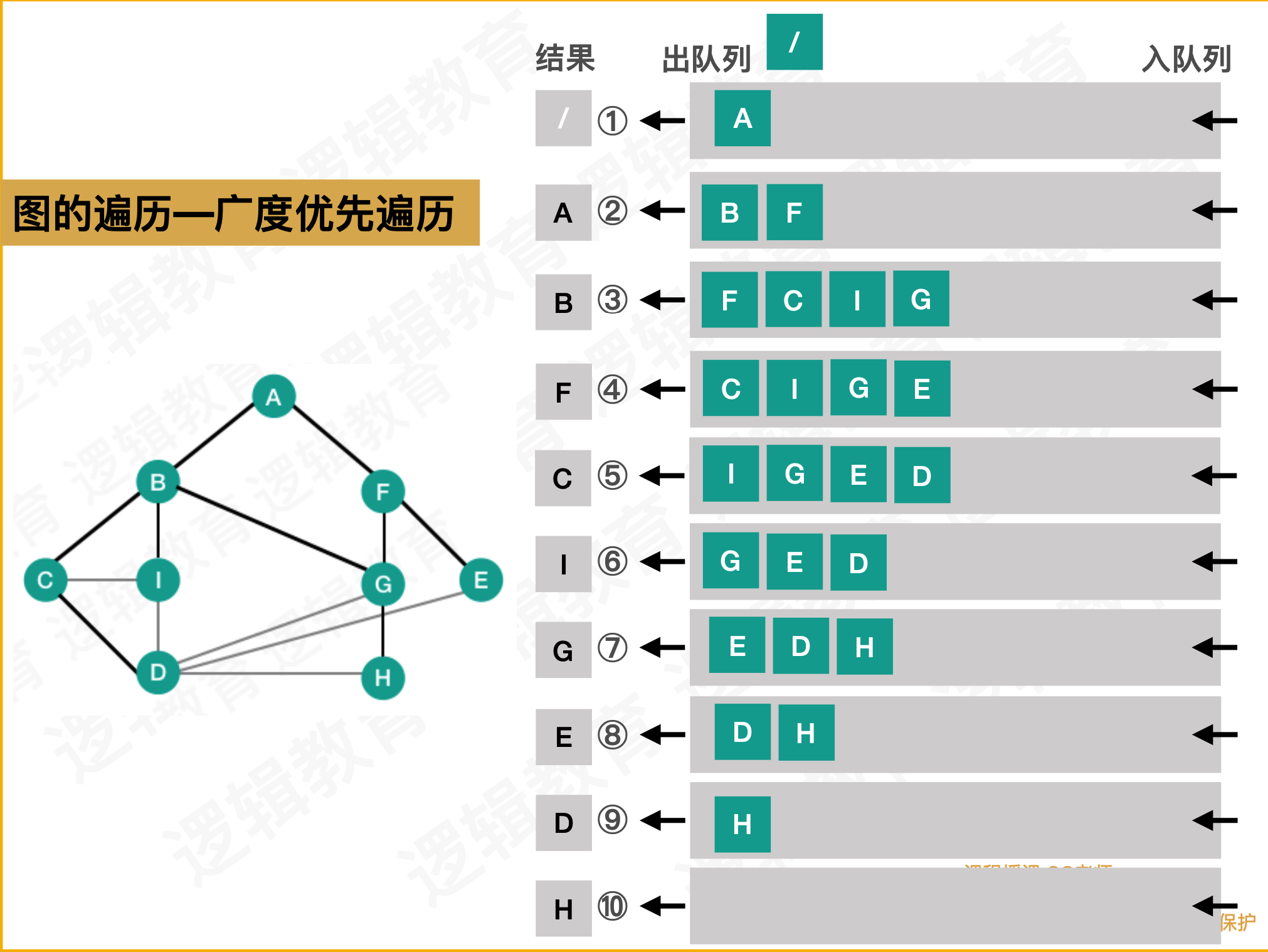
邻接矩阵广度优先遍历代码实现逻辑
#include <stdio.h> #include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ #define MAXSIZE 9 /* 存储空间初始分配量 */ #define MAXEDGE 15 #define MAXVEX 9 #define INFINITYC 65535 typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numVertexes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; /*4.1 构建一个邻接矩阵*/ void CreateMGraph(MGraph *G) { int i, j; //1. 确定图的顶点数以及边数 G->numEdges=15; G->numVertexes=9; /*2.读入顶点信息,建立顶点表 */ G->vexs[0]='A'; G->vexs[1]='B'; G->vexs[2]='C'; G->vexs[3]='D'; G->vexs[4]='E'; G->vexs[5]='F'; G->vexs[6]='G'; G->vexs[7]='H'; G->vexs[8]='I'; /*3. 初始化图中的边表*/ for (i = 0; i < G->numVertexes; i++) { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } } /*4.将图中的连接信息输入到边表中*/ G->arc[0][1]=1; G->arc[0][5]=1; G->arc[1][2]=1; G->arc[1][8]=1; G->arc[1][6]=1; G->arc[2][3]=1; G->arc[2][8]=1; G->arc[3][4]=1; G->arc[3][7]=1; G->arc[3][6]=1; G->arc[3][8]=1; G->arc[4][5]=1; G->arc[4][7]=1; G->arc[5][6]=1; G->arc[6][7]=1; /*5.无向图是对称矩阵.构成对称*/ for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /* 4.2 ***需要用到的队列结构与相关功能函数*** */ /* 循环队列的顺序存储结构 */ typedef struct { int data[MAXSIZE]; int front; /* 头指针 */ int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */ }Queue; /* 初始化一个空队列Q */ Status InitQueue(Queue *Q) { Q->front=0; Q->rear=0; return OK; } /* 若队列Q为空队列,则返回TRUE,否则返回FALSE */ Status QueueEmpty(Queue Q) { if(Q.front==Q.rear) /* 队列空的标志 */ return TRUE; else return FALSE; } /* 若队列未满,则插入元素e为Q新的队尾元素 */ Status EnQueue(Queue *Q,int e) { if ((Q->rear+1)%MAXSIZE == Q->front) /* 队列满的判断 */ return ERROR; Q->data[Q->rear]=e; /* 将元素e赋值给队尾 */ Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } /* 若队列不空,则删除Q中队头元素,用e返回其值 */ Status DeQueue(Queue *Q,int *e) { if (Q->front == Q->rear) /* 队列空的判断 */ return ERROR; *e=Q->data[Q->front]; /* 将队头元素赋值给e */ Q->front=(Q->front+1)%MAXSIZE; /* front指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } /******** Queue End **************/ /*4.3 邻接矩阵广度优先遍历-代码实现*/ Boolean visited[MAXVEX]; /* 访问标志的数组 */ void BFSTraverse(MGraph G){ int temp = 0; //1. Queue Q; InitQueue(&Q); //2.将访问标志数组全部置为"未访问状态FALSE" for (int i = 0 ; i < G.numVertexes; i++) { visited[i] = FALSE; } //3.对遍历邻接表中的每一个顶点(对于连通图只会执行1次,这个循环是针对非连通图) for (int i = 0 ; i < G.numVertexes; i++) { if(!visited[i]){ visited[i] = TRUE; printf("%c ",G.vexs[i]); //4. 入队 EnQueue(&Q, i); while (!QueueEmpty(Q)) { //出队 DeQueue(&Q, &i); for (int j = 0; j < G.numVertexes; j++) { if(G.arc[i][j] == 1 && !visited[j]) { visited[j] = TRUE; printf("%c ",G.vexs[j]); EnQueue(&Q, j); } } } } } } int main(int argc, const char * argv[]) { // insert code here... printf("邻接矩阵广度优先遍历!\n"); MGraph G; CreateMGraph(&G); BFSTraverse(G); printf("\n"); return 0; }
4:邻接表广度优先遍历代码实现逻辑
#include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 9 /* 存储空间初始分配量 */ #define MAXEDGE 15 #define MAXVEX 9 #define INFINITYC 65535 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */ typedef char VertexType; /* 顶点类型应由用户定义 */ typedef int EdgeType; /* 边上的权值类型应由用户定义 */ /* 邻接矩阵结构 */ typedef struct { VertexType vexs[MAXVEX]; /* 顶点表 */ EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */ int numVertexes, numEdges; /* 图中当前的顶点数和边数 */ }MGraph; /* 邻接表结构****************** */ typedef struct EdgeNode /* 边表结点 */ { int adjvex; /* 邻接点域,存储该顶点对应的下标 */ int weight; /* 用于存储权值,对于非网图可以不需要 */ struct EdgeNode *next; /* 链域,指向下一个邻接点 */ }EdgeNode; typedef struct VertexNode /* 顶点表结点 */ { int in; /* 顶点入度 */ char data; /* 顶点域,存储顶点信息 */ EdgeNode *firstedge;/* 边表头指针 */ }VertexNode, AdjList[MAXVEX]; typedef struct { AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */ }graphAdjList,*GraphAdjList; /*4.1 构建一个邻接矩阵*/ void CreateMGraph(MGraph *G) { int i, j; //1. 确定图的顶点数以及边数 G->numEdges=15; G->numVertexes=9; /*2.读入顶点信息,建立顶点表 */ G->vexs[0]='A'; G->vexs[1]='B'; G->vexs[2]='C'; G->vexs[3]='D'; G->vexs[4]='E'; G->vexs[5]='F'; G->vexs[6]='G'; G->vexs[7]='H'; G->vexs[8]='I'; /*3. 初始化图中的边表*/ for (i = 0; i < G->numVertexes; i++) { for ( j = 0; j < G->numVertexes; j++) { G->arc[i][j]=0; } } /*4.将图中的连接信息输入到边表中*/ G->arc[0][1]=1; G->arc[0][5]=1; G->arc[1][2]=1; G->arc[1][8]=1; G->arc[1][6]=1; G->arc[2][3]=1; G->arc[2][8]=1; G->arc[3][4]=1; G->arc[3][7]=1; G->arc[3][6]=1; G->arc[3][8]=1; G->arc[4][5]=1; G->arc[4][7]=1; G->arc[5][6]=1; G->arc[6][7]=1; /*5.无向图是对称矩阵.构成对称*/ for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /*4.2 利用邻接矩阵构建邻接表*/ void CreateALGraph(MGraph G,GraphAdjList *GL){ //1.创建邻接表,并且设计邻接表的顶点数以及弧数 *GL = (GraphAdjList)malloc(sizeof(graphAdjList)); (*GL)->numVertexes = G.numVertexes; (*GL)->numEdges = G.numEdges; //2. 从邻接矩阵中将顶点信息输入 for (int i = 0; i < G.numVertexes; i++) { //顶点入度为0 (*GL)->adjList[i].in = 0; //顶点信息 (*GL)->adjList[i].data = G.vexs[i]; //顶点边表置空 (*GL)->adjList[i].firstedge = NULL; } //3. 建立边表 EdgeNode *e; for (int i = 0; i < G.numVertexes; i++) { for (int j = 0; j < G.numVertexes; j++) { if (G.arc[i][j] == 1) { //创建边表中的邻近结点 i->j e = (EdgeNode *)malloc(sizeof(EdgeNode)); //邻接序号为j e->adjvex = j; //将当前结点的指向adjList[i]的顶点边表上 e->next = (*GL)->adjList[i].firstedge; (*GL)->adjList[i].firstedge = e; //顶点j 上的入度++; (*GL)->adjList[j].in++; // //创建边表中的邻近结点 j->i // e = (EdgeNode *)malloc(sizeof(EdgeNode)); // //邻接序号为j // e->adjvex = i; // //将当前结点的指向adjList[i]的顶点边表上 // e->next = (*GL)->adjList[j].firstedge; // (*GL)->adjList[j].firstedge = e; // //顶点j 上的入度++; // (*GL)->adjList[i].in++; } } } } /* 5.2 ***需要用到的队列结构与相关功能函数*** */ /* 循环队列的顺序存储结构 */ typedef struct { int data[MAXSIZE]; int front; /* 头指针 */ int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */ }Queue; /* 初始化一个空队列Q */ Status InitQueue(Queue *Q) { Q->front=0; Q->rear=0; return OK; } /* 若队列Q为空队列,则返回TRUE,否则返回FALSE */ Status QueueEmpty(Queue Q) { if(Q.front==Q.rear) /* 队列空的标志 */ return TRUE; else return FALSE; } /* 若队列未满,则插入元素e为Q新的队尾元素 */ Status EnQueue(Queue *Q,int e) { if ((Q->rear+1)%MAXSIZE == Q->front) /* 队列满的判断 */ return ERROR; Q->data[Q->rear]=e; /* 将元素e赋值给队尾 */ Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } /* 若队列不空,则删除Q中队头元素,用e返回其值 */ Status DeQueue(Queue *Q,int *e) { if (Q->front == Q->rear) /* 队列空的判断 */ return ERROR; *e=Q->data[Q->front]; /* 将队头元素赋值给e */ Q->front=(Q->front+1)%MAXSIZE; /* front指针向后移一位置, */ /* 若到最后则转到数组头部 */ return OK; } /* *********************** Queue End ******************************* */ /*5.3 邻接表广度优先遍历*/ Boolean visited[MAXSIZE]; /* 访问标志的数组 */ void BFSTraverse(GraphAdjList GL){ //1.创建结点 EdgeNode *p; Queue Q; InitQueue(&Q); //2.将访问标志数组全部置为"未访问状态FALSE" for(int i = 0; i < GL->numVertexes; i++) visited[i] = FALSE; //3.对遍历邻接表中的每一个顶点(对于连通图只会执行1次,这个循环是针对非连通图) for(int i = 0 ;i < GL->numVertexes;i++){ //4.判断当前结点是否被访问过. if(!visited[i]){ visited[i] = TRUE; //打印顶点 printf("%c ",GL->adjList[i].data); EnQueue(&Q, i); while (!QueueEmpty(Q)) { DeQueue(&Q, &i); p = GL->adjList[i].firstedge; while (p) { //判断 if(!visited[p->adjvex]){ visited[p->adjvex] = TRUE; printf("%c ",GL->adjList[p->adjvex].data); EnQueue(&Q, p->adjvex); } p = p->next; } } } } } int main(int argc, const char * argv[]) { // insert code here... printf("邻接表广度优先遍历\n"); MGraph G; GraphAdjList GL; CreateMGraph(&G); CreateALGraph(G,&GL); BFSTraverse(GL); printf("\n"); return 0; }
注意




