08*：字符串匹配算法：BF算法与RK算法（RK算法主要的解决思路就是在BF算法的基础上，将子串转换成哈希值来进行比较，它算是BF算法的升级版。）
问题
字符串匹配问题: 给你⼀个仅包含⼩写字⺟的字符串主串S = "abcacabdc",和模式串T = "abd", 请查找出模式串在主串第 ⼀次出现的位置; 提示: 主串和模式串均为⼩写字⺟且都是合法输⼊。
目录
1：BF算法-暴风匹配算法
2：RK算法
3：去除重复字母
预备
正文
1：BF算法-暴风匹配算法
思路:
1：分别利用计数指针i和j指示主串S和模式T中当前正待比较的字符位置,i初值为pos,j的初值为1;
2：如果2个串均为比较到串尾,即i和j均小于等于S和T的长度时, 则循环执行以下的操作:
S[i]和T[j]比较,若相等,则i 和 j分别指示串中下一个位置,继续比较后续的字符;
若不相等,指针后退重新开始匹配.
S[i]和T[j]比较,若相等,则i 和 j分别指示串中下一个位置,继续比较后续的字符;
若不相等,指针后退重新开始匹配.
从主串的下一个字符串(i = i - j + 2)起再重新和模式第一个字符(j = 1)比较;
3：如果j > T.length, 说明模式T中的每个字符串依次和主串S找中的一个连续字符序列相等,则匹配成功,返回和模式T中第一个字符的字符在主串S中的序号(i-T.length);否则匹配失败,返回0;
代码实现
#include "string.h" #include "stdio.h" #include "stdlib.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 40 /* 存储空间初始分配量 */ typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */ typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */ typedef char String[MAXSIZE+1]; /* 0号单元存放串的长度 */ /* 生成一个其值等于chars的串T */ Status StrAssign(String T,char *chars) { int i; if(strlen(chars)>MAXSIZE) return ERROR; else { T[0]=strlen(chars); for(i=1;i<=T[0];i++) T[i]=*(chars+i-1); return OK; } } Status ClearString(String S) { S[0]=0;/* 令串长为零 */ return OK; } /* 输出字符串T。 */ void StrPrint(String T) { int i; for(i=1;i<=T[0];i++) printf("%c",T[i]); printf("\n"); } /* 输出Next数组值。 */ void NextPrint(int next[],int length) { int i; for(i=1;i<=length;i++) printf("%d",next[i]); printf("\n"); } /* 返回串的元素个数 */ int StrLength(String S) { return S[0]; } /* 1. BF算法-爆发匹配算法 思路: 1. 分别利用计数指针i和j指示主串S和模式T中当前正待比较的字符位置,i初值为pos,j的初值为1; 2. 如果2个串均为比较到串尾,即i和j均小于等于S和T的长度时, 则循环执行以下的操作: * S[i]和T[j]比较,若相等,则i 和 j分别指示串中下一个位置,继续比较后续的字符; * 若不相等,指针后退重新开始匹配. 从主串的下一个字符串(i = i - j + 2)起再重新和模式第一个字符(j = 1)比较; 3. 如果j > T.length, 说明模式T中的每个字符串依次和主串S找中的一个连续字符序列相等,则匹配成功,返回和模式T中第一个字符的字符在主串S中的序号(i-T.length);否则匹配失败,返回0; */ int Index_BF(String S, String T,int pos){ //i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 int i = pos; //j用于子串T中当前位置下标值 int j = 1; //若i小于S的长度并且j小于T的长度时，循环继续 while (i <= S[0] && j <= T[0]) { //比较的2个字母相等,则继续比较 if (S[i] == T[j]) { i++; j++; }else { //不相等,则指针后退重新匹配 //i 退回到上次匹配的首位的下一位; //加1,因为是子串的首位是1开始计算; //再加1的元素,从上次匹配的首位的下一位; i = i-j+2; //j 退回到子串T的首位 j = 1; }} //如果j>T[0],则找到了匹配模式 if (j > T[0]) { //i母串遍历的位置 - 模式字符串长度 = index 位置 return i - T[0]; }else{ return -1; } } int main(int argc, const char * argv[]) { // insert code here... printf("字符串模式匹配!\n"); int i,*p; String s1,s2; // StrAssign(s1, "abcdex"); StrAssign(s1, "abcacabdc"); printf("s1子串为"); StrPrint(s1); // StrAssign(s2, "xe"); StrAssign(s2, "abd"); printf("s2子串为"); StrPrint(s2); i = Index_BF(s1, s2, 1); printf("i = %d\n",i); return 0; }
2：RK算法
1：Hash (哈希)
一般中文也翻译做”散列”; 也可以直接音译”哈希”;
散列在开发中是常见手段! 比如大家常用的MD5 算法就是哈希算法;
哈希算法在安全方面应用是非常多,一般体现在如下这几个方面:
- 文件校验
- 数字签名
- 鉴权协议
2：RK算法的基本思想
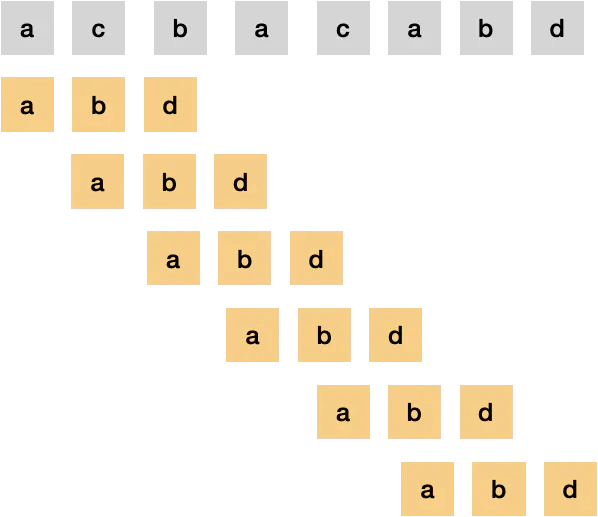
主串根据模式串长度，拆分成n个长度为模式串长度的子串，然后比较子串和模式串的哈希值（散列值）
HASH！
如果两个字符串hash后的值不相同，则它们肯定不相同；如果它们hash后的值相同，它们不一定相同。
RK算法的基本思想就是：将模式串P的hash值跟主串S中的每一个长度为|P|的子串的hash值比较。如果不同，则它们肯定不相等；如果相同，则再诸位比较之。
优势是：
- 把母串以模式串的长度等分，然后比较子串的哈希值
- 一边计算子串的哈希值，一边比较，并不是先计算出所有的子串的哈希值，再去比较
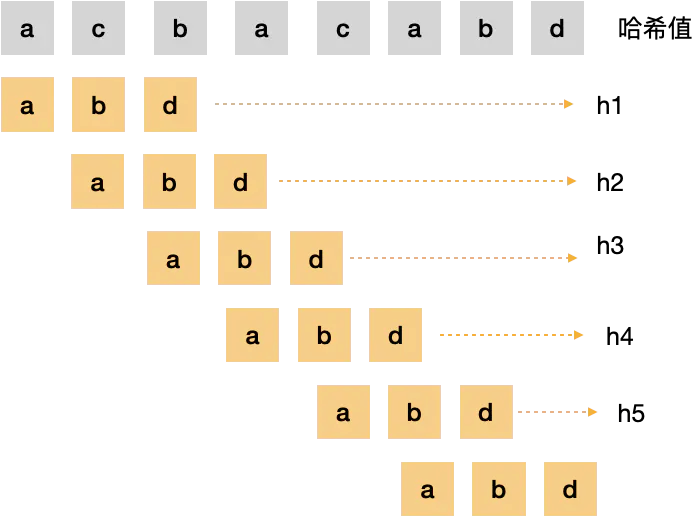
3：哈希值
将不同的字符组合能够通过某种公式的计算映射成不同的数字!
例如
比较 “abc” 与 “cde” ; 比较 123 与 456; 是一样的吗?
657 = 6 *10 * 10 + 5 * 10 + 7 * 1
657 = 6 * 10^2 + 5 *10^1 + 7 *10^0
4：所以字母换算成哈希值
"cba ” = ‘c’ * 26*26 + ‘b’ * 26 + ‘a’ * 1
= 2 * 26 * 26 + 126 + 0 * 1
= 1378
RK 算法核⼼思想
“ cba ” = c✖26*2 + b ✖ 26*1 + a ✖26*0
= 2 ✖ 26*2 + 1 ✖ 26*1 + 0 ✖26*0
= 1352 + 26 + 0
= 1378
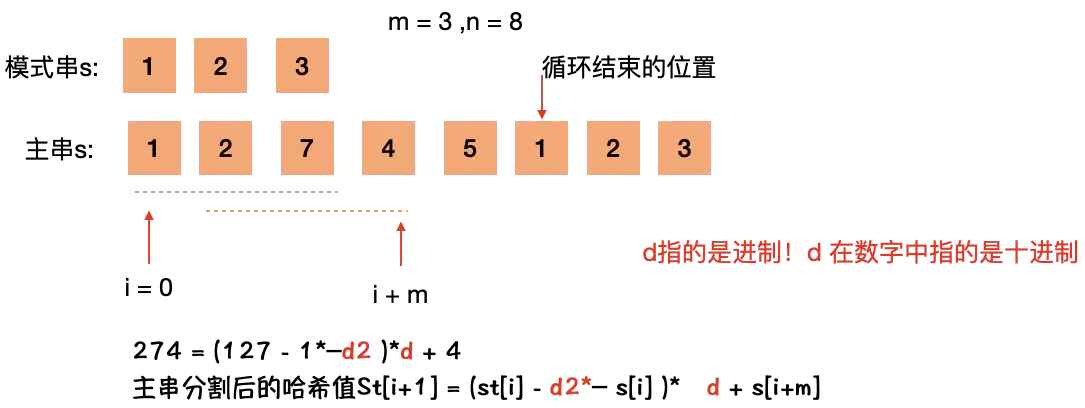
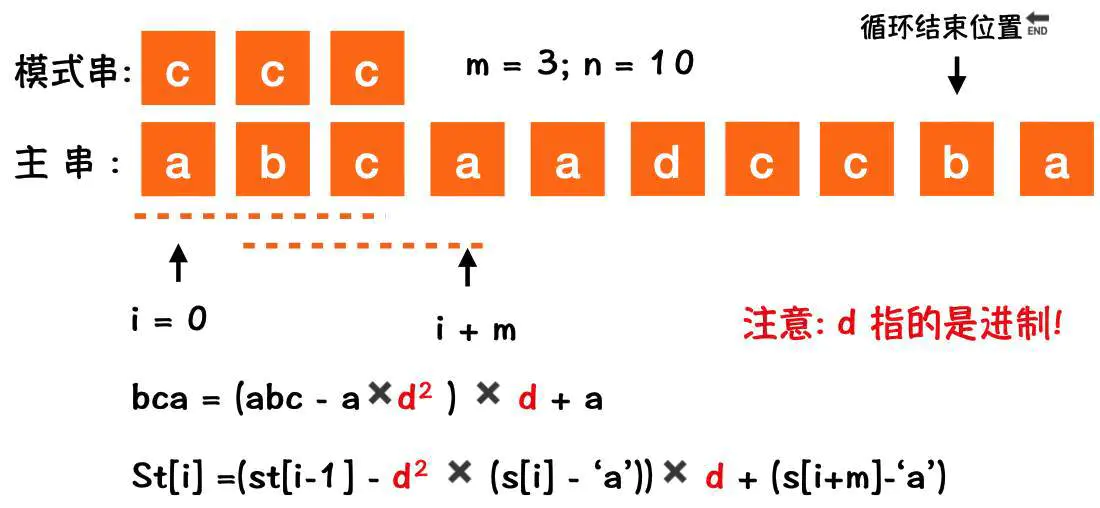
5：子串哈希值求解规律: 相邻哈希值的规律，减少计算的次数
相邻的2个子串 s[i] 与 s[i+1] (i表示子串从主串中的起始位置,子串的长度
都为m). 对应的哈希值计算公式有交集. 也就说我们可以使用s[i-1]计算出s[i]
的哈希值;
s[i] = 1 ✖ 10*2 + 2✖10*1 + 7 ✖10*0
s[i+1] = 2 ✖ 10*2 + 7✖10*1 + 4 ✖10*0
s[i+1] = 10 ✖ (127 - 1✖10*2 ) + 4
s[i+1] = 10 ✖ (s[i] - 1✖10*2 ) + 4
s[i+1] 实现上是上一个s[i]去掉最高位数据,其余的m-1为字符乘以
d进制. 再加上最后一个为字符得到;
6：哈希冲突
如果相等时,不要直接返回结果. 而是重新核实!
设计更复杂的哈希公式
- 如果不做哈希冲突二次核查 比较次数是n-m+1次; 那么时间复杂度为O(n);
- 但是要想解决冲突存在可能性.就需要添加二次核查! 那么 就需要m次比对; 那么时间复杂度为O(n*m);
7：代码实现
#include <stdio.h> #include <stdlib.h> #include <string.h> //d 表示进制 #define d 26 //4.为了杜绝哈希冲突. 当前发现模式串和子串的HashValue 是一样的时候.还是需要二次确认2个字符串是否相等. int isMatch(char *S, int i, char *P, int m) { int is, ip; for(is=i, ip=0; is != m && ip != m; is++, ip++) if(S[is] != P[ip]) return 0; return 1; } //3.算出最d进制下的最高位 //d^(m-1)位的值; int getMaxValue(int m){ int h = 1; for(int i = 0;i < m - 1;i++){ h = (h*d); } return h; } /* * 字符串匹配的RK算法 * Author：Rabin & Karp * 若成功匹配返回主串中的偏移，否则返回-1 */ int RK(char *S, char *P) { //1. n:主串长度, m:子串长度 int m = (int) strlen(P); int n = (int) strlen(S); printf("主串长度为:%d,子串长度为:%d\n",n,m); //A.模式串的哈希值; St.主串分解子串的哈希值; unsigned int A = 0; unsigned int St = 0; //2.求得子串与主串中0~m字符串的哈希值[计算子串与主串0-m的哈希值] //循环[0,m)获取模式串A的HashValue以及主串第一个[0,m)的HashValue //此时主串:"abcaadddabceeffccdd" 它的[0,2)是ab //此时模式串:"cc" //cc = 2 * 26^1 + 2 *26 ^0 = 52+2 = 54; //ab = 0 * 26^1 + 1 *26^0 = 0+1 = 1; for(int i = 0; i != m; i++){ //第一次 A = 0*26+2; //第二次 A = 2*26+2; A = (d*A + (P[i] - 'a')); //第一次 st = 0*26+0 //第二次 st = 0*26+1 St = (d*St + (S[i] - 'a')); } //3. 获取d^m-1值(因为经常要用d^m-1进制值) int hValue = getMaxValue(m); //4.遍历[0,n-m], 判断模式串HashValue A是否和其他子串的HashValue 一致. //不一致则继续求得下一个HashValue //如果一致则进行二次确认判断,2个字符串是否真正相等.反正哈希值冲突导致错误 //注意细节: //① 在进入循环时,就已经得到子串的哈希值以及主串的[0,m)的哈希值,可以直接进行第一轮比较; //② 哈希值相等后,再次用字符串进行比较.防止哈希值冲突; //③ 如果不相等,利用在循环之前已经计算好的st[0] 来计算后面的st[1]; //④ 在对比过程,并不是一次性把所有的主串子串都求解好Hash值. 而是是借助s[i]来求解s[i+1] . 简单说就是一边比较哈希值,一边计算哈希值; for(int i = 0; i <= n-m; i++){ if(A == St) if(isMatch(S,i,P,m)) //加1原因,从1开始数 return i+1; St = (St - hValue*(S[i]-'a'))*d + (S[i+m]-'a'); } return -1; } int main() { char *buf="abcababcabx"; char *ptrn="abcabx"; printf("主串为%s\n",buf); printf("子串为%s\n",ptrn); int index = RK(buf, ptrn); printf("find index : %d\n",index); return 1; }
总结
RK算法主要的解决思路就是在BF算法的基础上，将子串转换成哈希值来进行比较，它算是BF算法的升级版。
3：算法—去除重复字母
给你一个仅包含小写字母的字符串，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证返回结果的字典序最小（要求不能打乱其他字符的相对位置）。
示例1: 输入:"bcabc"， 输出:"abc"
示例2: 输入:"cbacdcbc"， 输出:"acdb"
示例1: 输入:"bcabc"， 输出:"abc"
示例2: 输入:"cbacdcbc"， 输出:"acdb"
字典序: 字符串之间比较和数字比较不一样; 字符串比较是从头往后挨个字符比较,那个字符串大取决于两个字符串中第一个对应不相等的字符; 例如 任意一个a开头的字符串都大于任意一个b开头的字符串;例如字典中apple 大于 book;
题目的意思,你去除重复字母后,需要按最小的字典序返回.并且不能打乱其他字母的相对位置;
例如 bcabc 你应该返回abc, 而不是bca,cab;
例如 cbacdcbc 应该返回acdb,而不是cbad,bacd,adcb
例如 zab,应该返回zab,而不是abz;
思路:
- 判断字符串可能出现的特殊情况
- 用一个record数组记录字符串中字母出现的次数;
- 申请一个字符串栈stack用来存储去除重复字母的结果,并利用它的特性帮助我们找到正确的次序;
- 遍历字符串s
- 从0~top,遍历stack 判断当前字符s[i]是否存在于栈stack中
如果当前字符是否存在于栈的定义一个falg 标记isExist, 0表示不存在, 1表示存在
6.如果isExist存在,record[s[i]]位置上的出现次数减一，并继续遍历下一个字符; 表示当前的stack已经有这个字符了没有必要处理这个重复的字母;
7.如果isExist不存在,则
如果不存在,则需要循环一个找到一个正确的位置,然后在存储起来;
如果不存在，跳过栈中所有比当前字符大、且后面还会出现的元素，然后将当前字符入栈
top > -1表示栈非空
stack[top] > s[i]表示栈顶元素比当前元素大
record[stack[top]] > 1表示后面还会出现
通过一个while循环找到将栈中位置错误的数据,出栈. 找当前合适的位置,则结束while循环;
找到合理的位置后,则将当前字符s[i]入栈;
8.直到遍历完所有字符后,则为字符串栈stack 添加一个结束符'\0',并返回当前字符串首地址;
char *removeDuplicateLetters(char *s) { /* ① 特殊情况处理,s为空,或者字符串长度为0; ② 特殊情况,s的长度为1,则没有必要后续的处理,则直接返回s; */ int len = (int)strlen(s); if (len < 1) { return "have no string"; } if (len == 1) { return s; } char record[26] = {0}; //record数组,用来记录字符串s中每个字符未来会出现的次数; //申请一个字符串stack;(用栈的特性来进行stack字符串的数据进出) char* stack = (char*)malloc((len+1) * sizeof(char)); //memset(void *s, int ch, size_t n) 将stack(len+1) *sizeof(char)长度范围的空间填充0; memset(stack, 0, (len+1) * sizeof(char)); //stack 栈顶赋初值为-1; int top = -1; int i; for (i = 0; i < len; i++) { //1.统计每个字符的频次 record[s[i] - 'a']++; } //2.遍历s,入栈 for (i = 0; i < len; i++) { //isExist 标记, 判断当前字符是否存在栈中; int isExist = 0; //①从0~top,遍历stack 判断当前字符s[i]是否存在于栈stack中 //如果当前字符是否存在于栈的flag, 0表示不存在, 1表示存在 //top指向栈顶(也是执行stack字符串最后一个字符的位置,表示字符串长度上限) for (int j = 0; j <= top; j++) { if (s[i] == stack[j]) { isExist = 1; break; } } //② 如果存在,record[s[i]]位置上的出现次数减一，并继续遍历下一个字符 //③ 如果不存在,则需要循环一个正确位置存储起来; //④ 如果不存在，跳过栈中所有比当前字符大、且后面还会出现的元素，然后将当前字符入栈 // top > -1表示栈非空 //stack[top] > s[i]表示栈顶元素比当前元素大 //record[stack[top]] > 1表示后面还会出现 //例如b,c因为不符合以下条件会直接入栈.stack[] = "bc",但是当当前字符是"a"时,由于bcabc,a不应该是在stack的顺序是"bca",所以要把位置不符合的字符出栈; //top = 1,stack[top] > s[i], c>a; 并且stack[top] 在之后还会重复的出现,所以我们可以安心的把stack中的栈顶C出栈,所以stack[]="b",top减一后等于0; 同时也需要将record[c]出现次数减一; //top=0,stack[top]>s[i],b>a,并且stack[top] 在之后还会出现,所以stack把栈顶b出栈,所以此时栈stack[]="",top减一后等于-1, 此时栈中位置不正确的字符都已经移除; if (isExist == 1) { record[s[i] - 'a']--; } else { while (top > -1 && stack[top] > s[i] && record[stack[top] - 'a'] > 1) { // 跳过该元素，频次要减一 record[stack[top] - 'a']--; // 出栈 top--; } //⑤ 结束while 循环; //循环结束的3种可能性:(1)移动到栈底(top == -1) ; (2)栈顶元素小于当前元素(stack[top] <= s[i]) (3)栈顶元素后面不出现(record[stack[top]] == 1) // 此时，当前元素要插入到top的下一个位置 // top往上移动1位 top++; // 入栈 stack[top] = s[i]; } } //结束栈顶添加字符结束符 stack[++top] = '\0'; return stack; } int main(int argc, const char * argv[]) { // insert code here... printf("去掉重复字母! LeetCode-困难 \n"); char *s ; s = removeDuplicateLetters("bcabc"); printf("%s\n",s);//abc s = removeDuplicateLetters("zab"); printf("%s\n",s);//zab s = removeDuplicateLetters("cbacdcbc"); printf("%s\n",s);//acdb printf("\n"); return 0; }
注意
