06*:队列结构的顺序与链式存储实现(1:队列、 2: 循环队列顺序队列 、3:链式队列)
问题
目录
1:队列
2:循环队列顺序队列
3:链式队列
预备
正文
一:队列
1:队列:
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
读取特性:“先入先出”,”后入后出“(FIFO)。
- 顺序队列:在顺序表的基础上实现的队列结构;
- 链队列:在链表的基础上实现的队列结构;
两者的区别仅是顺序表和链表的区别,即在实际的物理空间中,数据集中存储的队列是顺序队列,分散存储的队列是链队列。
3:顺序存储队列假溢出
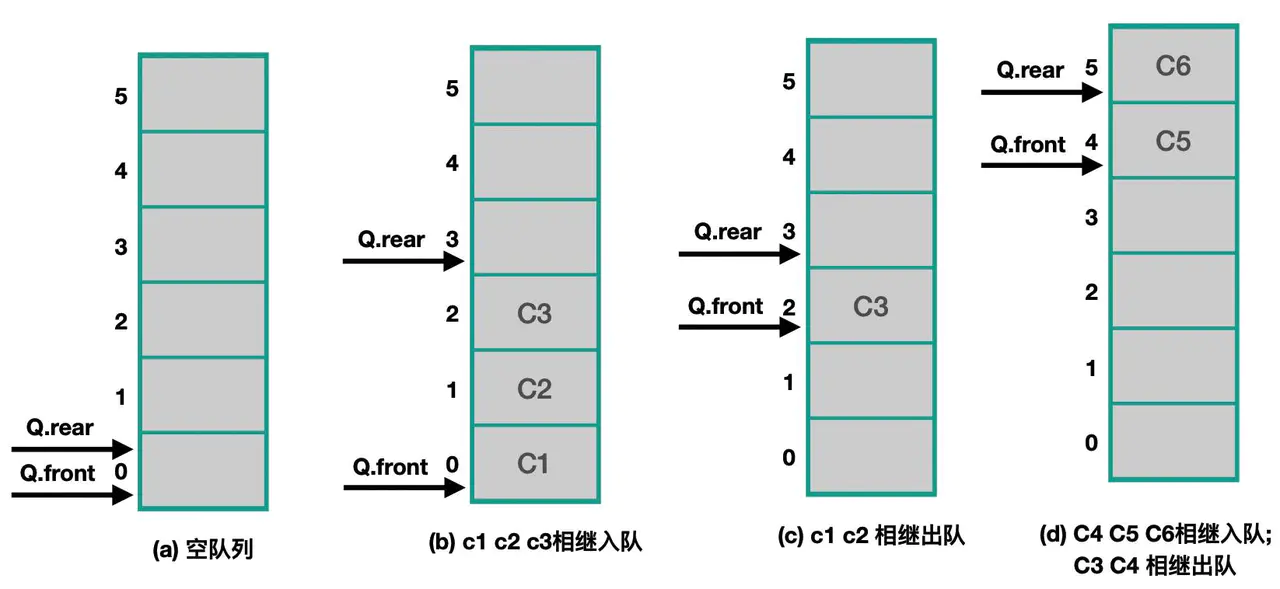
如上图,这个队列中的总个数为6个,但目前如果接着入队的话,会导致数组越界的错误,但是队列在下标为0,1,2,3的位置是没有元素的,造成了空间浪费。我们把这种现象叫做“假溢出”。
为了解决“假溢出”的问题,我们引入循环队列。
4:循环队列
就是队后面满了,再从头开始,也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。

此时问题又来了,如上图第4个,队满时发现rear指针与front重合了,刚才说了,当rear=front时,表示是空队列,现在当队列满时,rear也等于front。那么如何判断队列到底是空的还是满的了?
解决办法为:当队列空时,判断条件就是rear=front, 当队列满时,我们修改其判断条件,保留一个元素空闲。也就是说,队列满时,数组中还有一个空闲单元。
由于rear可能比front大,也可能比front小,所以假设队列的最大尺寸为MaxSize, 队列满的判断条件改为(rear + 1)% MaxSize = front. 队列的长度为(rear - front + MaxSize)% MaxSize.
二:循环队列顺序存储
1:循环队列的顺序存储结构
typedef int Status; typedef int QElemType; /* QElemType类型根据实际情况而定,这里假设为int */ /* 循环队列的顺序存储结构 */ typedef struct { QElemType data[MAXSIZE]; int front; /* 头指针 */ int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */ }SqQueue;
2:循环对列顺序存储初始化
Status InitQueue(SqQueue *Q){ Q->front = 0; Q->rear = 0; return OK; }
3:循环对列顺序存储清空
Status ClearQueue(SqQueue *Q){ Q->front = Q->rear = 0; return OK; }
4:循环对列顺序存储判空
Status QueueEmpty(SqQueue Q){ //队空标记 if (Q.front == Q.rear) return TRUE; else return FALSE; }
5:循环对列顺序存储的长度
int QueueLength(SqQueue Q){ return (Q.rear - Q.front + MAXSIZE)%MAXSIZE; }
6:循环队列 顺序存储的对头元素
Status GetHead(SqQueue Q,QElemType *e){ //队列已空 if (Q.front == Q.rear) return ERROR; *e = Q.data[Q.front]; return OK; }
7:循环队列 顺序存储入队元素
Status EnQueue(SqQueue *Q,QElemType e){ //队列已满 if((Q->rear+1)%MAXSIZE == Q->front) return ERROR; //将元素e赋值给队尾 Q->data[Q->rear] = e; //rear指针向后移动一位,若到最后则转到数组头部; Q->rear = (Q->rear+1)%MAXSIZE; return OK; }
8:循环队列顺序存储出队
Status DeQueue(SqQueue *Q,QElemType *e){ //判断队列是否为空 if (Q->front == Q->rear) { return ERROR; } //将队头元素赋值给e *e = Q->data[Q->front]; //front 指针向后移动一位,若到最后则转到数组头部 Q->front = (Q->front+1)%MAXSIZE; return OK; }
9:循环队列 顺序存储遍历
Status QueueTraverse(SqQueue Q){ int i; i = Q.front; while ((i+Q.front) != Q.rear) { printf("%d ",Q.data[i]); i = (i+1)%MAXSIZE; } /* while ((i+Q.front)%MAXSIZE != Q.rear) { printf("%d ",Q.data[(i+Q.front)%MAXSIZE]); i = (i+1)%MAXSIZE; } */ printf("\n"); return OK; }
三:链式队列
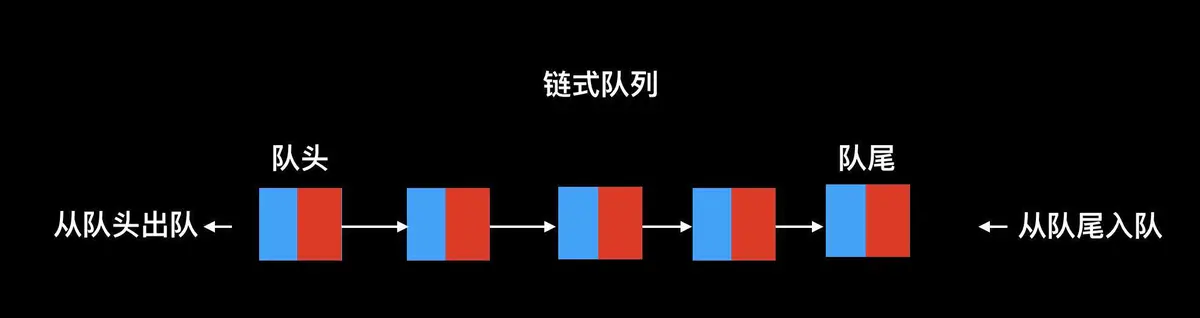
核心:
进入队列 :Q.rear尾节点后追加新节点,将Q.rear指向新节点,新节点成队尾;
出队列:Q.front指向的首元节点出队列,Q.front指向首元节点的下一个节点
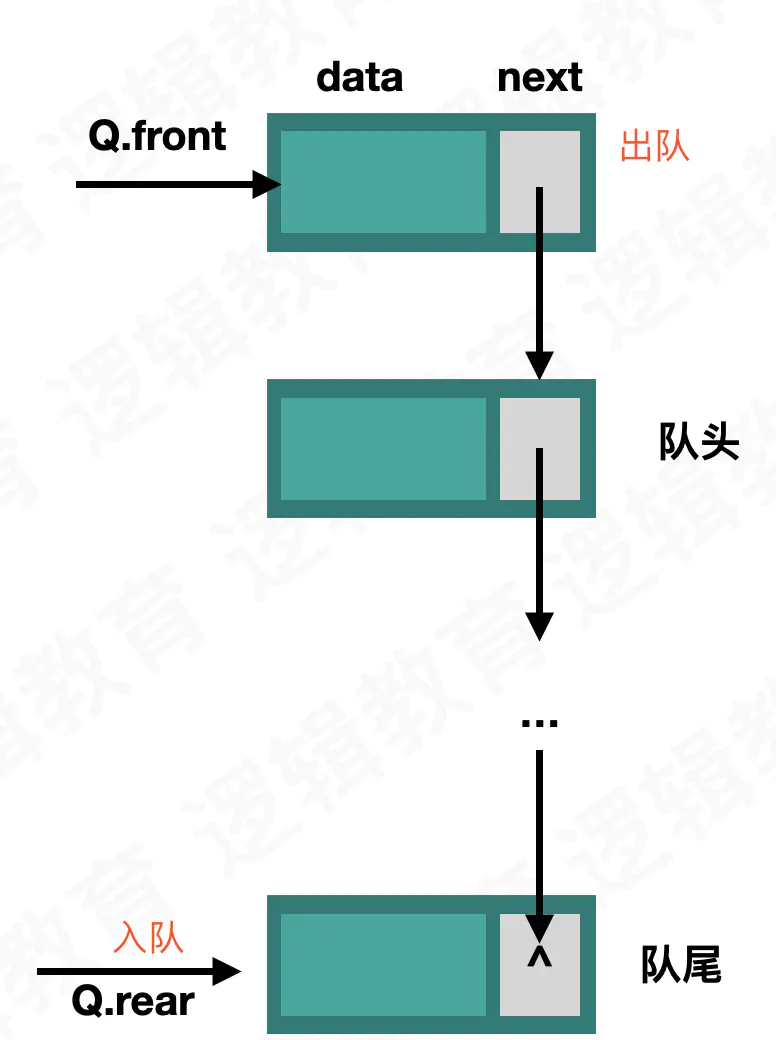
1:队列链式存储结点结构
typedef struct QNode /* 结点结构 */ { QElemType data; struct QNode *next; }QNode,*QueuePtr; typedef struct /* 队列的链表结构 */ { QueuePtr front,rear; /* 队头、队尾指针 */ }LinkQueue;
2:队列链式存储初始化
Status InitQueue(LinkQueue *Q){ //1. 头/尾指针都指向新生成的结点 Q->front = Q->rear = (QueuePtr)malloc(sizeof(QNode)); //2.判断是否创建新结点成功与否 if (!Q->front) { return ERROR; } //3.头结点的指针域置空 Q->front->next = NULL; return OK; }
3:队列链式存储销毁对列
Status DestoryQueue(LinkQueue *Q){ //遍历整个队列,销毁队列的每个结点 while (Q->front) { Q->rear = Q->front->next; free(Q->front); Q->front = Q->rear; } return OK; }
4:队列链式存储置空
Status ClearQueue(LinkQueue *Q){ QueuePtr p,q; Q->rear = Q->front; p = Q->front->next; Q->front->next = NULL; while (p) { q = p; p = p->next; free(q); } return OK; }
5:队列链式存储判空
Status QueueEmpty(LinkQueue Q){ if (Q.front == Q.rear) return TRUE; else return FALSE; }
6:队列链式存储的长度
int QueueLength(LinkQueue Q){ int i= 0; QueuePtr p; p = Q.front; while (Q.rear != p) { i++; p = p->next; } return i; }
7:队列链式存储入队
Status EnQueue(LinkQueue *Q,QElemType e){ //为入队元素分配结点空间,用指针s指向; QueuePtr s = (QueuePtr)malloc(sizeof(QNode)); //判断是否分配成功 if (!s) { return ERROR; } //将新结点s指定数据域. s->data = e; s->next = NULL; //将新结点插入到队尾 Q->rear->next = s; //修改队尾指针 Q->rear = s; return OK; }
8:队列链式存储出队
Status DeQueue(LinkQueue *Q,QElemType *e){ QueuePtr p; //判断队列是否为空; if (Q->front == Q->rear) { return ERROR; } //将要删除的队头结点暂时存储在p p = Q->front->next; //将要删除的队头结点的值赋值给e *e = p->data; //将原队列头结点的后继p->next 赋值给头结点后继 Q->front->next = p ->next; //若队头就是队尾,则删除后将rear指向头结点. if(Q->rear == p) Q->rear = Q->front; free(p); return OK; }
9:队列链式存储头元素
Status GetHead(LinkQueue Q,QElemType *e){ //队列非空 if (Q.front != Q.rear) { //返回队头元素的值,队头指针不变 *e = Q.front->next->data; return TRUE; } return FALSE; }
10:队列链式存储遍历
Status QueueTraverse(LinkQueue Q){ QueuePtr p; p = Q.front->next; while (p) { printf("%d ",p->data); p = p->next; } printf("\n"); return OK; }
总结
对于循环队列与链队列的比较,可以从两方面来考虑,从时间上,其实它们的基本操作都是常数时间,即都为O(1)的,不过循环队列是事先申请好空间,使用期间不释放,而对于链队列,每次申请和释放结点也会存在一些时间开销,如果入队出队频繁,则两者还是有细微差异。对于空间上来说,循环队列必须有一个固定的长度,所以就有了存储元素个数和空间浪费的问题。而链队列不存在这个问题,尽管它需要一个指针域,会产生一些空间上的开销,但也可以接受。所以在空间上,链队列更加灵活。
总的来说,在可以确定队列长度最大值的情况下,建议用循环队列,如果你无法预估队列的长度时,则用链队列。
栈和队列也都可以通过链式存储结构来实现,实现原则上与线性表基本相同如图所示。
注意





