05*:栈结构的顺序以及链式存储实现(1:栈 2:顺序栈 3:链式栈 4:递归 )
问题
目录
1:栈
2:顺序栈
3:链式栈
4:递归
预备
正文
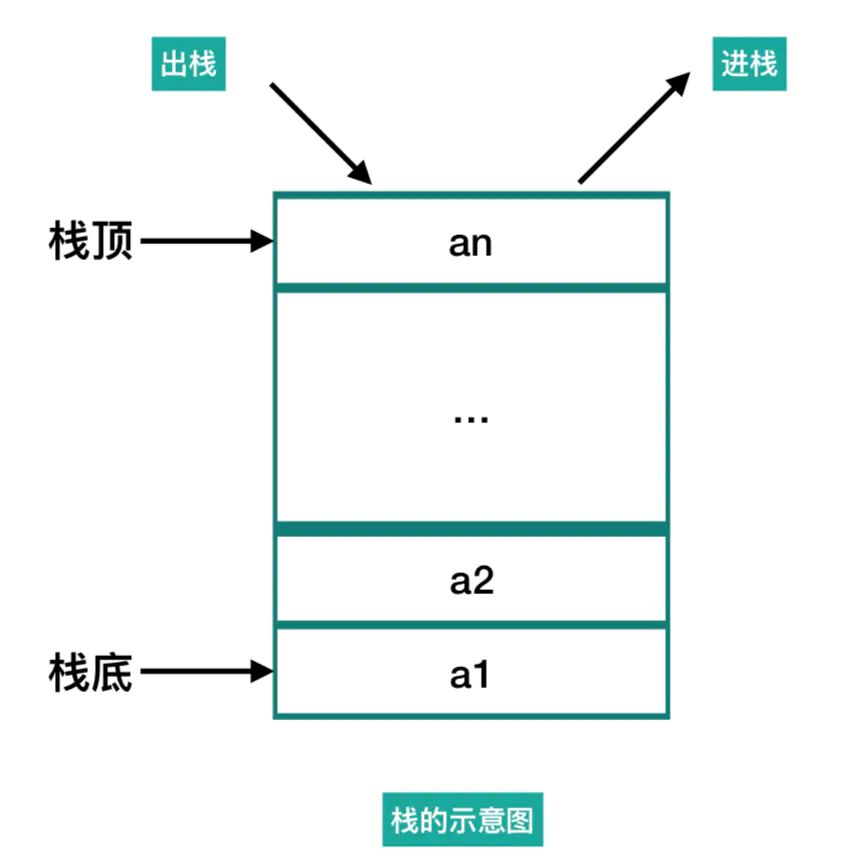
一:栈
1:定义
栈是一种特殊的线性结构,先进后出,只能在一段进行操作,我们把允许插入和删除的一端称为栈顶,另一端称为栈底。
- 不含任何数据元素的栈称为空栈。
- 栈的插入操作叫做进栈,也叫做压栈、入栈
- 栈的删除操作,叫做出栈,也叫做弹栈。
- 我们一般吧运行操作的一端叫做top(栈顶),并用一个变量进行标示
/* 顺序栈结构 */ typedef struct { SElemType data[MAXSIZE]; int top; /* 用于栈顶指针 */ }SqStack;
二:顺序栈操作
既然栈是一种数据结构,那么它必然也有自己的操作接口:
| 操作结构 | 功能 | |
|---|---|---|
| size() | 报告栈的规模 | |
| empty() | 判断栈是否为空 | |
| push(e) | 将元素 e 插至栈顶(入栈) | |
| pop() | 删除栈顶对象,并返回该对象的引用(出栈) | |
| top() | 引用栈顶对象 |
进栈&出栈
在实际应用中通常只会对栈执行以下两种操作:
• 向栈中添加元素,此过程被称为"进栈"(入栈或压栈)
• 栈中提取出指定元素,此过程被称为"出栈"(或弹栈)
栈的具体实现
栈是一种 "特殊" 的线性存储结构,因此栈的具体实现有以下两种方式:
• 顺序栈:采用顺序存储结构可以模拟栈存储数据的特点,从而实现栈存储结构;
• 链栈:采用链式存储结构实现栈结构;
两种实现方式的区别,仅限于数据元素在实际物理空间上存放的相对位置,顺序栈底层采用的是数组,链栈底层采用的是链表.
顺序栈
1:创建一个空栈
Status initStack(SqStack *S){ S->top = -1 ; return OK; }
2:判断栈是否为空
Status StackEmpty(SqStack S){ if (S.top == -1) return TRUE; else return FALSE; }
3:置空栈
将栈置空,不需要将顺序栈的元素都清空,只需要修改top标签就可以了.
Status ClearStack(SqStack *S){ S->top = -1; return OK; }
4:栈的长度
int StackLength(SqStack S){ return S.top + 1; }
5:获取栈顶元素
Status GetTop(SqStack S,SElemType *e){ if (S.top == -1) return ERROR; else *e = S.data[S.top]; return OK; }
6:插入元素到栈顶(入栈)
Status PushData(SqStack *S, SElemType e){ //栈已满 if (S->top == MAXSIZE -1) { return ERROR; } //栈顶指针+1; S->top ++; //将新插入的元素赋值给栈顶空间 S->data[S->top] = e; return OK; }
7:删除栈顶元素(出栈)
Status Pop(SqStack *S,SElemType *e){ //空栈,则返回error; if (S->top == -1) { return ERROR; } //将要删除的栈顶元素赋值给e *e = S->data[S->top]; //栈顶指针--; S->top--; return OK; }
8:遍历栈元素
Status StackTraverse(SqStack S){ int i = 0; printf("此栈中所有元素"); while (i<=S.top) { printf("%d ",S.data[i++]); } printf("\n"); return OK; }
三:链栈
链式栈:就是一种操作受限的单向链表
链式栈的操作一般含有:出栈、入栈、栈的初始化、判断栈是否为空、清空
链式栈:新一个节点->将新建节点的指针域指向原栈顶节点->将栈顶指针移动到新建节
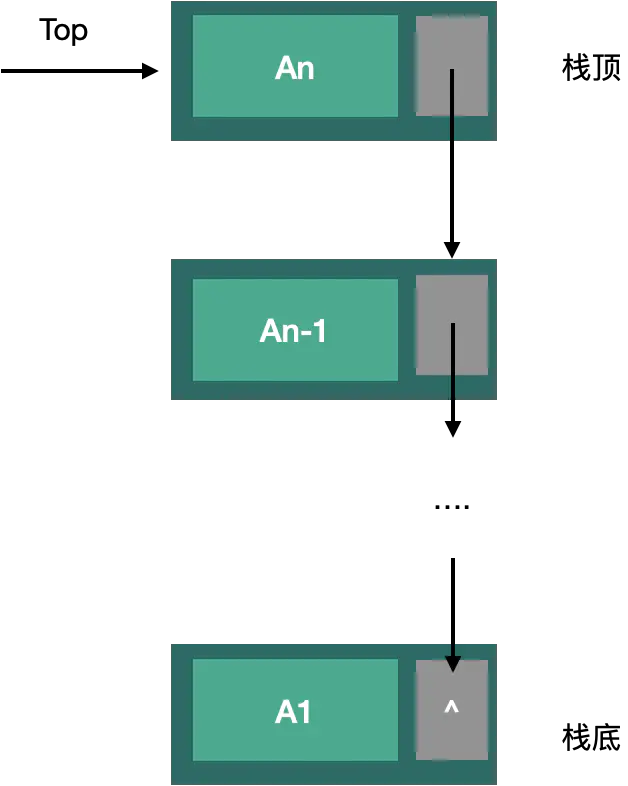
链式栈就是以链式存储的形式的栈,因为是链式结构,所以就不存在下标的说法,也不存在容量的问题,所以top是以指针形式指向栈顶的元素,并且因为栈是先进后出的,所以需要用前插法进行插入操作
1:定义
/* 链栈结构 */ 定义节点 typedef struct StackNode { SElemType data; struct StackNode *next; }StackNode,*LinkStackPtr; 定义链式栈结构 typedef struct { LinkStackPtr top; int count; }LinkStack;
2:链式栈的初始化
/*构造一个空栈S */ Status InitStack(LinkStack *S) { *S = (LinkStack )malloc(ziseof(StackNode)); if(*S->top == NULL){ return ERROR ; } S->top=NULL; S->count=0; return OK; }
3:链式栈的置空
Status ClearStack(LinkStack *S){ LinkStackPtr p,q; p = S->top; while (p) { q = p; p = p->next; free(q); } S->count = 0; return OK; }
4:链式栈的长度
int StackLength(LinkStack S){ return S.count;
}
5: 链式栈的是否为空
Status StackEmpty(LinkStack S){ if (S.count == 0) return TRUE; else return FALSE; }
6:链式栈的获取栈顶元素
Status GetTop(LinkStack S,SElemType *e){ if(S.top == NULL) return ERROR; else *e = S.top->data; return OK; }
7:链式栈的插入元素到栈顶位置
1:新建结点temp,赋值
2:把新结点temp的next指向制定指针top。temp->next = s->top
3:更新栈顶指针top s->top = temp
4:栈S的count++
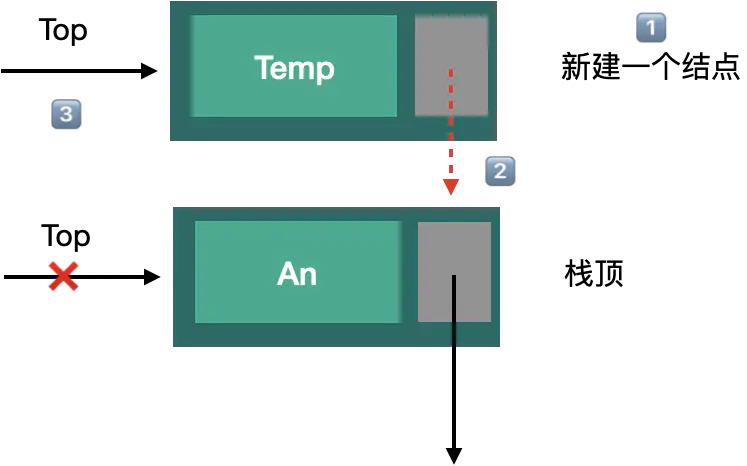
Status Push(LinkStack *S, SElemType e){ //创建新结点temp LinkStackPtr temp = (LinkStackPtr)malloc(sizeof(StackNode)); //赋值 temp->data = e; //把当前的栈顶元素赋值给新结点的直接后继, 参考图例第①步骤; temp->next = S->top; //将新结点temp 赋值给栈顶指针,参考图例第②步骤; S->top = temp; S->count++; return OK; }
8:链式栈的删除栈顶元素
- 新建节点p指向S->top
- 栈顶指针下移一位, 指向后一结点 S->top= S->top->next
- 释放p free(p);
- S->count--
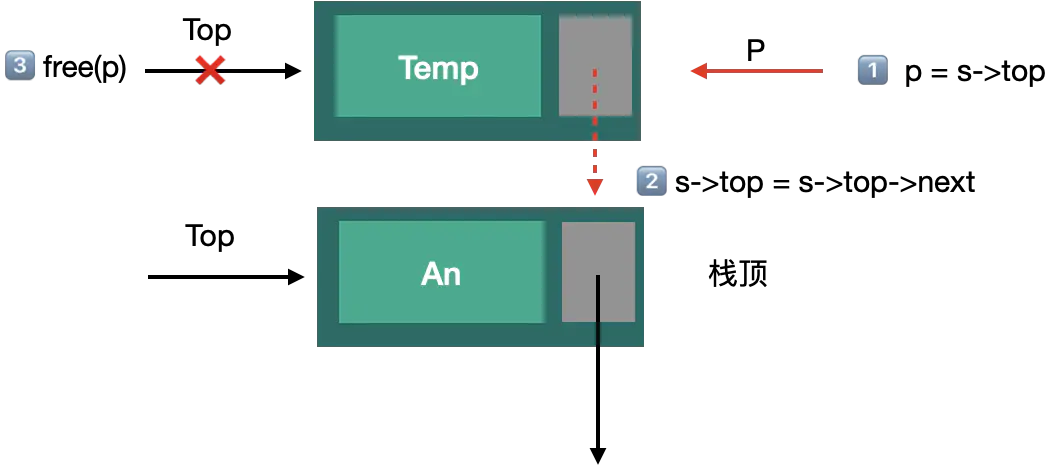
/*5.7 若栈不为空,则删除S的栈顶元素,用e返回其值. 并返回OK,否则返回ERROR*/ Status Pop(LinkStack *S,SElemType *e){ LinkStackPtr p; if (StackEmpty(*S)) { return ERROR; } //将栈顶元素赋值给*e *e = S->top->data; //将栈顶结点赋值给p,参考图例① p = S->top; //使得栈顶指针下移一位, 指向后一结点. 参考图例② S->top= S->top->next; //释放p free(p); //个数-- S->count--; return OK; }
9:链式栈的遍历
Status StackTraverse(LinkStack S){ LinkStackPtr p; p = S.top; while (p) { printf("%d ",p->data); p = p->next; } printf("\n"); return OK; }
顺序栈与链栈
- 对比一下顺序栈与链栈,它们在时间复杂度上是一样的,均为O(1)。
- 顺序栈需要事先确定一个固定的长度,可能会存在内存空间浪费的问题,但它的优势是存取时定位很方便。
- 链栈则要求每个元素都有指针域,这同时也增加了一些内存开销,但对于栈的长度无限制。
- 所以它们的区别和线性表中讨论的一样,如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈会更好一些。
四:栈和递归
1:递归的基本思想
所谓递归,就是有去有回。
递归的基本思想,是把规模较大的一个问题,分解成规模较小的多个子问题去解决,而每一个子问题又可以继续拆分成多个更小的子问题。
最重要的一点就是假设子问题已经解决了,现在要基于已经解决的子问题来解决当前问题;或者说,必须先解决子问题,再基于子问题来解决当前问题
直接或者间接调用本身就是递归
2:什么场景下使用递归
• 定义是本身就是递归 :阶乘、斐波拉契数列
• 数据结构式递归的 链表的数据结构定义(指针域)
其数据结构本身具有递归特点
例如,对于链表其结点Node的定义是由数据域date和指针域next组成,而其指针域next是一种指向Node类的指针,即Node的定义中用到了本身,所以链表是一种递归的数据结构
• 问题是递归的 汉诺塔问题
3:分治法解决递归问题的条件
• 一个大的问题可以差分成一个晓得问题,并且小问题的实现和大问题高度的雷同
• 通过分治,可以简化问题的解决
• 必须要有一个递归出口、递归边界
4:函数调用看递归函数栈
funcA{
funcB();
}
funcB{
funcC();
}
funcC{
}
调用函数A;
调用函数B;
调用函数C;
函数C返回;
函数B返回;
函数A返回;
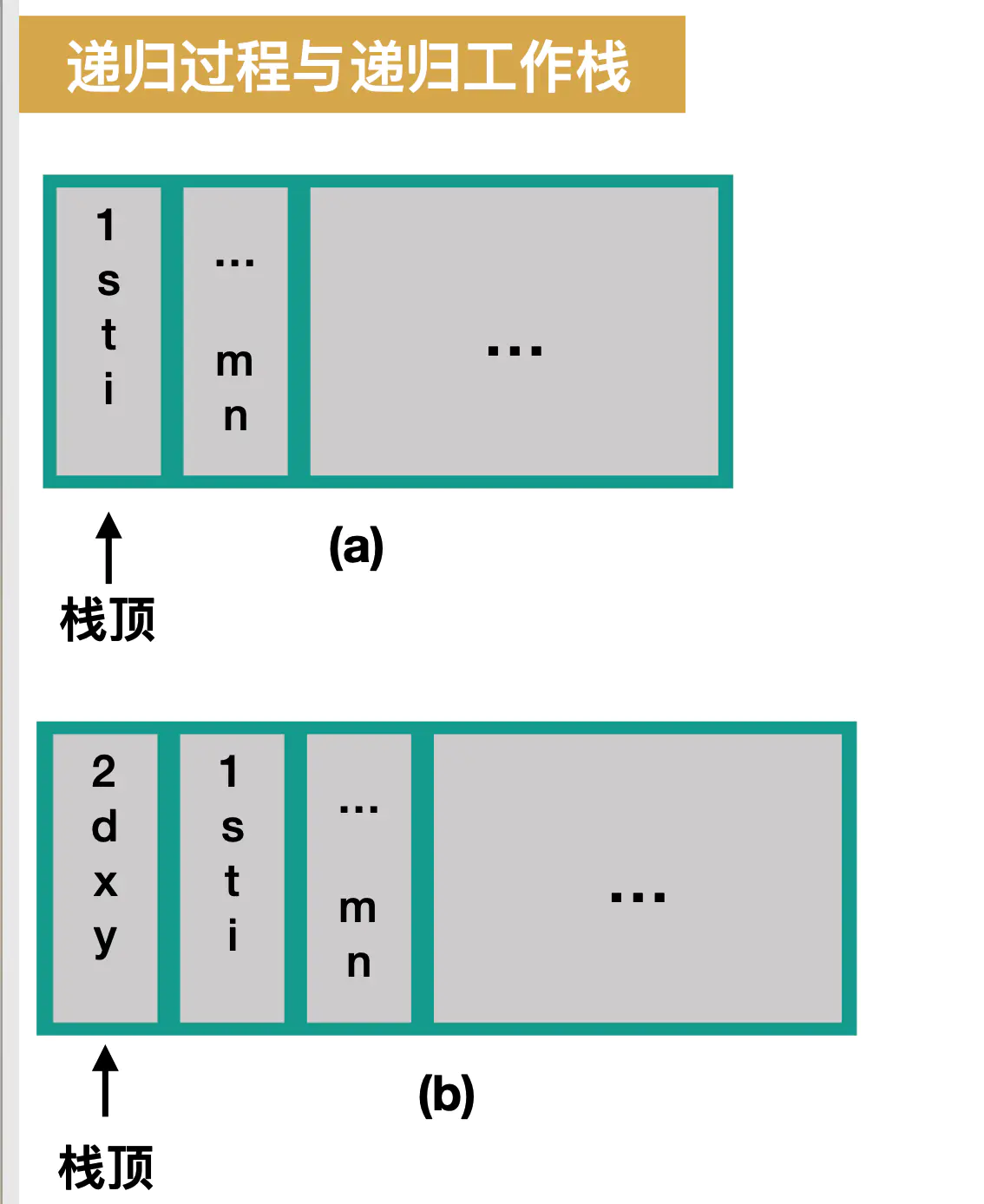
一个函数在运行期间调用另一个函数,在运行被调用函数之前,系统需要先完成3件事情:
• 把所有的实参和函数的返回地址信息传递给被调用的函数保存起来(栈空间)
• 为被调用函数的局部变量分配存储空间
• 把代码编译的控制权交给被调用函数
被调用函数返回调用函数之前,系统做的3件事情:
• 保存被调用函数的计算结构
• 释放被调用函数的数据去
• 根据保存的返回地址信息把控制权交给调用函数
int second(int d){ int x,y; //... } int first(int s ,int t){ int i; //... second(i) //2.⼊入栈 //... } void main( ){ int m,n; first(m ,n); //1.⼊入栈 //... }
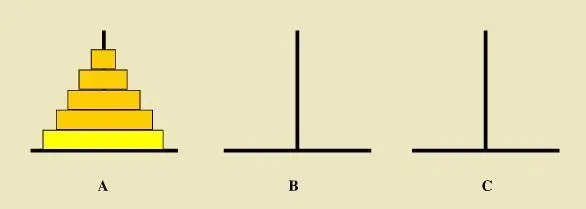
6:汉诺塔问题
从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数
解:(1)n == 1
第1次 1号盘 A---->C sum = 1 次
(2) n == 2
第1次 1号盘 A---->B
第2次 2号盘 A---->C
第3次 1号盘 B---->C sum = 3 次
(3)n == 3
第1次 1号盘 A---->C
第2次 2号盘 A---->B
第3次 1号盘 C---->B
第4次 3号盘 A---->C
第5次 1号盘 B---->A
第6次 2号盘 B---->C
第7次 1号盘 A---->C sum = 7 次
不难发现规律:1个圆盘的次数 2的1次方减1
2个圆盘的次数 2的2次方减1
3个圆盘的次数 2的3次方减1
n个圆盘的次数 2的n次方减1
故:移动次数为:2^n - 1
从主线程开始调用方法(函数)进行不停的压栈和出栈操作,函数的调用就是将函数压如栈中,函数的结束就是函数出栈的过程,这样就保证了方法调用的顺序流,即当函数出现多层嵌套时,需要从外到内一层层把函数压入栈中,最后栈顶的函数先执行结束(最内层的函数先执行结束)后出栈,再倒数第二层的函数执行结束出栈,到最后,第一个进栈的函数调用结束后从栈中弹出回到主线程,并且结束。
8:算法分析(递归算法):
我们在利用计算机求汉诺塔问题时,必不可少的一步是对整个实现求解进行算法分析。到目前为止,求解汉诺塔问题最简单的算法还是同过递归来求,至于是什么是递归,递归实现的机制是什么,我们说的简单点就是自己是一个方法或者说是函数,但是在自己这个函数里有调用自己这个函数的语句,而这个调用怎么才能调用结束呢?,这里还必须有一个结束点,或者具体的说是在调用到某一次后函数能返回一个确定的值,接着倒数第二个就能返回一个确定的值,一直到第一次调用的这个函数能返回一个确定的值。
(1) 把n-1个盘子由A 移到 B;
(2) 把第n个盘子由 A移到 C;
(3) 把n-1个盘子由B 移到 C;
从这里入手,在加上上面数学问题解法的分析,我们不难发现,移到的步数必定为奇数步:
(1)中间的一步是把最大的一个盘子由A移到C上去;
(2)中间一步之上可以看成把A上n-1个盘子通过借助辅助塔(C塔)移到了B上,
(3)中间一步之下可以看成把B上n-1个盘子通过借助辅助塔(A塔)移到了C上;
int m = 0; void moves(char X,int n,char Y){ m++; printf("%d: from %c ——> %c \n",n,X,Y); } //n为当前盘子编号. ABC为塔盘 void Hanoi(int n ,char A,char B,char C){ //目标: 将塔盘A上的圆盘按规则移动到塔盘C上,B作为辅助塔盘; //将编号为1的圆盘从A移动到C上 if(n==1) moves(A, 1, C); else { //将塔盘A上的编号为1至n-1的圆盘移动到塔盘B上,C作为辅助塔; Hanoi(n-1, A, C, B); //将编号为n的圆盘从A移动到C上; moves(A, n, C); //将塔盘B上的编号为1至n-1的圆盘移动到塔盘C上,A作为辅助塔; Hanoi(n-1, B, A, C); } } Hanoi(4, 'A', 'B', 'C'); printf("盘子数量为4:一共实现搬到次数:%d\n",m); 1: from A ——> B 2: from A ——> C 1: from B ——> C 3: from A ——> B 1: from C ——> A 2: from C ——> B 1: from A ——> B 4: from A ——> C 1: from B ——> C 2: from B ——> A 1: from C ——> A 3: from B ——> C 1: from A ——> B 2: from A ——> C 1: from B ——> C 盘子数量为4:一共实现搬到次数:15
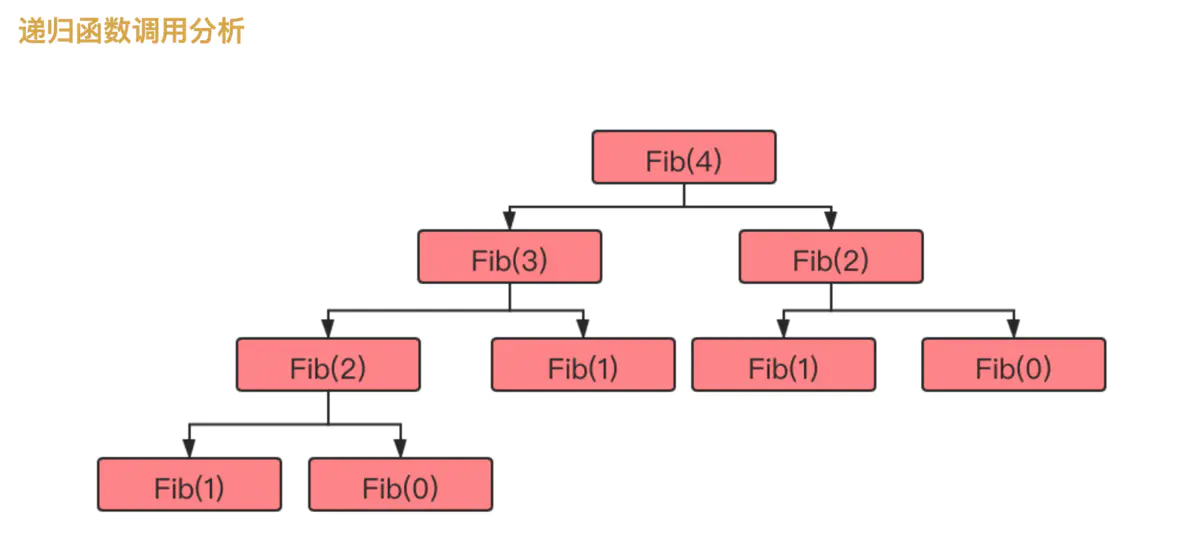
9:斐波拉契数列
int Fbi(int i){ if(i<2) return i == 0?0:1; return Fbi(i-1)+Fbi(i-2); } for (int i =0; i < 10; i++) { printf("%d ",Fbi(i)); }
注意





