算法效率的度量方法
算法效率的度量方法
注: 本系列笔记的图片来自小甲鱼的[数据结构与算法]
之前提到设计算法要尽量提高效率,这里的效率高一般指的是算法的执行时间.
事后统计法
通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低.
缺陷:
- 必须依据算法实现编制好测试程序
- 不同测试环境差别不是一般的大
事前分析估算方法
在j计算机程序编写前,依据统计方法对算法进行估算.
经过总结,我们发现一个高级语言编写的程序在计算机上运行时所消耗的时间取决于下列因素:
- 算法采用的策略和方案
- 编译产生的代码质量
- 问题的输入规模
- 机器执行指令的速度
由此可见,抛开这些与计算机硬件,软件有关的因素,一个程序的运行时间依赖于算法的好坏和问题的输入规模.(所谓的问题输入规模是指输入量的多少)
例如,计算等差序列1-100的和:
// 第一种
int i, sum = 0, n = 100; // 执行1次
for( i = 1; i<= n; i++ ) // 执行n+1次
{
sum = sum + i; // 执行n次
}
// 第二种
int sum = 0, n = 100; // 执行1次
sum = (1+n)*n/2 // 执行1次
// 第一种算法执行了1+(n+1)+n=2n+2次
// 第二种算法执行了1+1=2次
如果我们把循环看做一个整体,忽略头尾判断的开销,那么这两个算法其实就是n和1的差距.
延申的例子:
int i, j, x=0, sum=0, n=100;
for( i=1; i <= n; i++ )
{
for( j=1; j <= n; j++ )
{
x++;
sum = sum + x;
}
}
这个例子中,循环条件i从1到100,每次都要让j循环100次,如果非常较真的研究总共精确执行次数,那是非常累的。
另一方面,我们研究算法的复杂度,侧重的是研究算法随着输入规模扩大增长量的一个抽象,而不是精确地定位需要执行多少次,因为如果这样的话,我们就又得考虑回编译器优化等问题,然后,然后就永远也没有然后了!
所以,对于刚才例子的算法,我们可以果断判定需要执行100²次。
我们不关心编写程序所用的语言是什么,也不关心这些程序将跑在什么样的计算机上,我们只关心它所实现的算法。
这样,不计那些循环索引的递增和循环终止条件、变量声明、打印结果等操作。最终,在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
我们在分析一个算法的运行时间时,重要的是把基本操作的数量和输入模式关联起来。
函数的渐近增长:
假设两个算法的输入规模都是n,算法A要做2n+3次操作,你可以这么理解:先执行n次的循环,执行完成后再有一个n次的循环,最后有3次运算。
算法B要做3n+1次操作,理解同上,你觉得它们哪一个更快些呢?
| 规模 | 算法A1 (2n+3) | 算法A2 (2n) | 算法B1 (3n+1) | 算法B2 (3n) |
|---|---|---|---|---|
| n=1 | 5 | 2 | 4 | 3 |
| n=2 | 7 | 4 | 7 | 6 |
| n=3 | 9 | 6 | 10 | 9 |
| n=10 | 23 | 20 | 31 | 30 |
| n=100 | 203 | 200 | 301 | 300 |
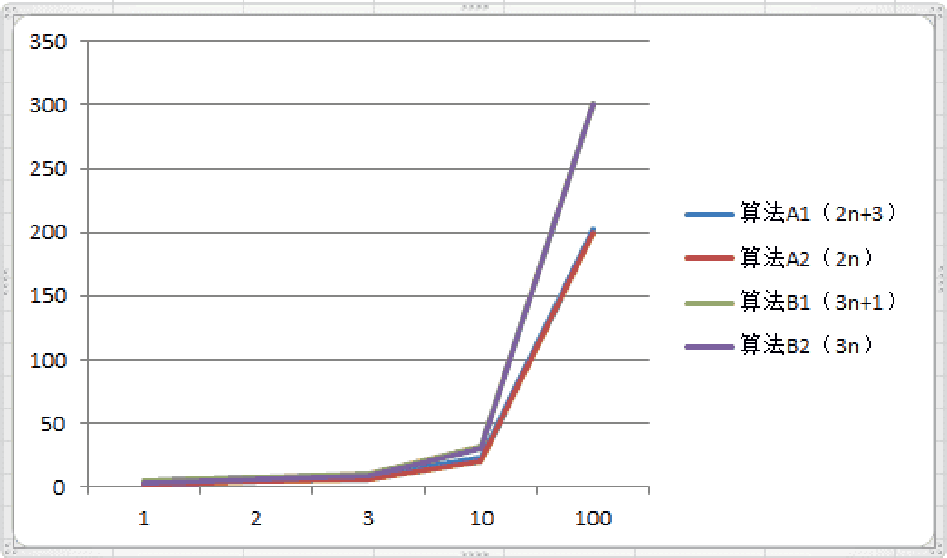
当n=1时,算法A1效率不如算法B1,当n=2时,两者效率相同;当n>2时,算法A1就开始优于算法B1了,随着n的继续增加,算法A1比算法B1逐步拉大差距。所以总体上算法A1比算法B1优秀。
A1和A2基本上是覆盖的,B1和B2基本上是覆盖的.
函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。
从刚才的对比中我们还发现,随着n的增大,后面的+3和+1其实是不影响最终的算法变化曲线的。所以,我们可以忽略这些加法常数。
第二个测试: 算法C是4n+8,算法D是2n²+1
| 次数 | 算法C1(4n+8) | 算法C2(n) | 算法D1(2n^2+1) | 算法D2(n^2) |
|---|---|---|---|---|
| n=1 | 12 | 1 | 3 | 1 |
| n=2 | 16 | 2 | 9 | 4 |
| n=3 | 20 | 3 | 19 | 9 |
| n=10 | 48 | 10 | 201 | 100 |
| n=100 | 408 | 100 | 20001 | 10000 |
| n=1000 | 4008 | 1000 | 2000001 | 1000000 |

我们观察发现,哪怕去掉与n相乘的常数,两者的结果还是没有改变,算法C2的次数随着n的增长,还是远小于算法D2。
也就是说,与最高次项相乘的常数并不重要,也可以忽略。
第三个测试: 算法E是2n2+3n+1,算法F是2n3+3n+1
| 次数 | 算法E1(2n^2+3n+1) | 算法E2(n^2) | 算法F1(2n^3+3n+1) | 算法F2(n^3) |
|---|---|---|---|---|
| n=1 | 6 | 1 | 6 | 1 |
| n=2 | 15 | 4 | 23 | 8 |
| n=3 | 28 | 9 | 64 | 27 |
| n=10 | 231 | 100 | 2031 | 1000 |
| n=100 | 20301 | 10000 | 2000301 | 1000000 |
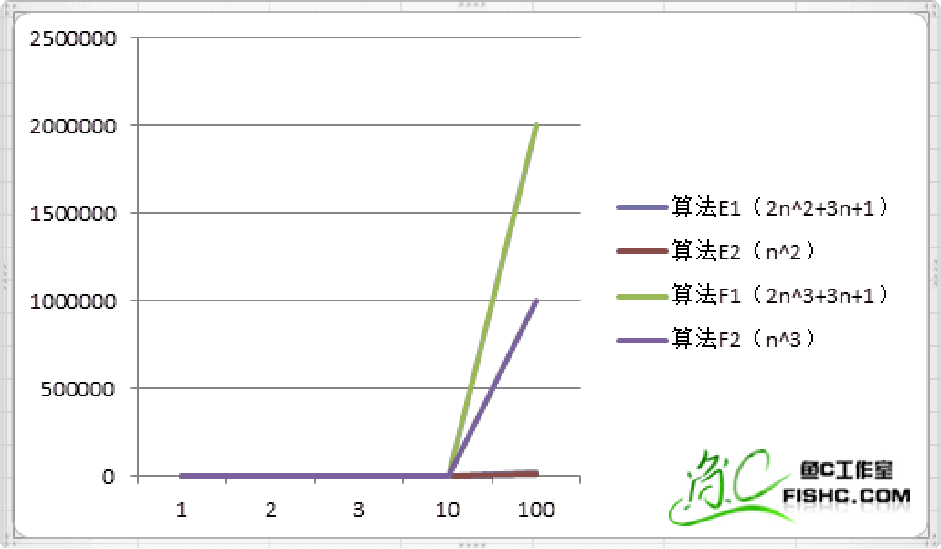
我们通过观察又发现,最高次项的指数大的,函数随着n的增长,结果也会变得增长特别快。而在比较算法E和F时,n的最高次项的乘数以及其余项均可以忽略
第四个测试:算法G是2n^2,算法H是3n+1,算法I是 2n^+3n+1
| 次数 | 算法G(2n^2) | 算法H(3n+1) | 算法I(2n^2+3n+1) |
|---|---|---|---|
| n=1 | 2 | 4 | 6 |
| n=2 | 8 | 7 | 15 |
| n=5 | 50 | 16 | 66 |
| n=10 | 200 | 31 | 231 |
| n=100 | 2000 | 301 | 20301 |
| n=1000 | 2000000 | 3001 | 200301 |
| n=10000 | 200000000 | 30001 | 200030001 |
| n=100000 | 20000000000 | 300001 | 20000300001 |
| n=1000000 | 2000000000000 | 3000001 | 2000003000001 |
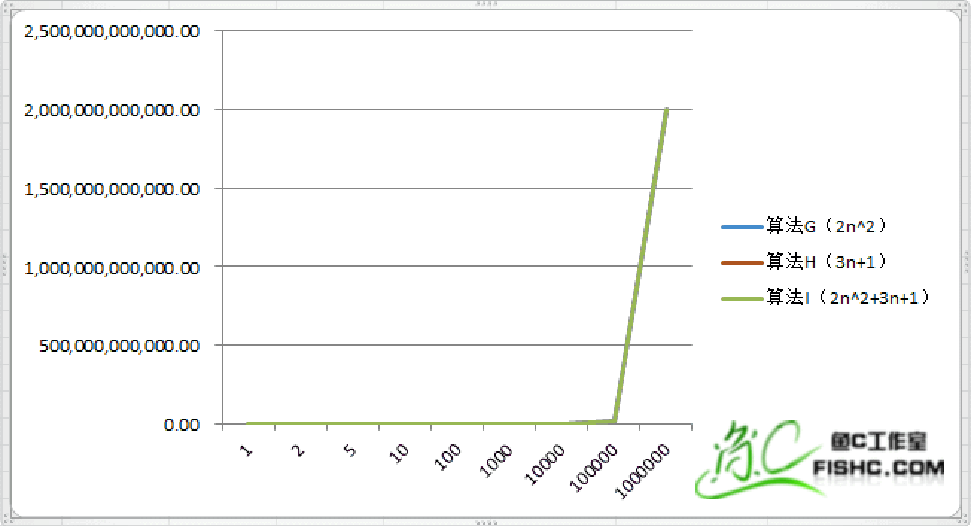
算法H已经看不到了,让我们看一下当数据量比较小的时候.
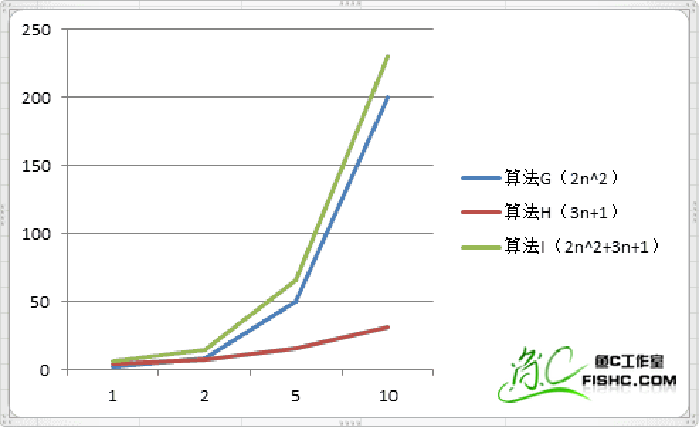
这组数据我们看得很清楚,当n的值变得非常大的时候,3n+1已经没法和2n^2的结果相比较,最终几乎可以忽略不计。而算法G跟算法I基本已经重合了。
于是我们可以得到这样一个结论,判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高项)的阶数。
注: 测试算法时需要大量的数据,越多越好.
算法时间复杂度
算法时间复杂度的定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度,记作:T(n)= O(f(n))。它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
关键需要知道执行次数==时间
这样用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。
一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
分析算法时间复杂度的步骤:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
- 得到的最后结果就是大O阶。
常数阶:
int sum = 0, n = 100;
printf(“常数阶\n”);
printf(“常数阶\n”);
printf(“常数阶\n”);
printf(“常数阶\n”);
printf(“常数阶\n”);
printf(“常数阶\n”);
sum = (1+n)*n/2;
按照概念"T(n)是关于问题规模n的函数",所以记作O(1).
线性阶:
一般含有非嵌套循环涉及线性阶,线性阶就是随着问题规模n的扩大,对应计算次数呈直线增长。
int i , n = 100, sum = 0;
for( i=0; i < n; i++ )
{
sum = sum + i;
}
上面这段代码,它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次。
平方阶:
int i, j, n = 100;
for( i=0; i < n; i++ )
{
for( j=0; j < n; j++ )
{
printf(“I love FishC.com\n”);
}
}
n等于100,也就是说外层循环每执行一次,内层循环就执行100次,那总共程序想要从这两个循环出来,需要执行100*100次,也就是n的平方。所以这段代码的时间复杂度为O(n^2)
如果,循环的次数不一样:
int i, j, n = 100;
for( i=0; i < n; i++ )
{
for( j=i; j < n; j++ )
{
printf(“不一样\n”);
}
}
由于当i=0时,内循环执行了n次,当i=1时,内循环则执行n-1次……当i=n-1时,内循环执行1次,所以总的执行次数应该是:
n+(n-1)+(n-2)+…+1 = n(n+1)/2 = n^2/2+n/2
忽略最高项n2的乘数以及其余项,得出O(n2).
总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
对数阶:
int i = 1, n = 100;
while( i < n )
{
i = i * 2;
}
由于每次i*2之后,就距离n更近一步,假设有x个2相乘后大于或等于n,则会退出循环。
于是由2^x = n得到x = log₂n,所以这个循环的时间复杂度为O(log₂n)。
函数调用的时间复杂度分析:
int i, j;
for(i=0; i < n; i++) { // 执行n+1次
function(i);
}
void function(int count) {
printf(“%d”, count); // 执行n次
}
// function函数的时间复杂度是O(1),所以整体的时间复杂度就是循环的次数O(n)
int i, j;
for(i=0; i < n; i++) {
function(i); // 执行n次
}
void function(int count) {
int j;
for(j=count; j < n; j++) {
printf(“%d”, j); // 执行n - count次
}
}
// count为0,1,2...n-1,函数的执行次数为n,n-1,..1,总次数n*(n+1)/2 =>算法的时间复杂度为O(n^2)
void function(int count) {
int j;
for(j=1; j < n; j++) {
printf(“%d”, j);
}
}
n++; // O(1)
function(n); // O(n)
for(i=0; i < n; i++) {
function(i); // O(n^2)
}
for(i=0; i < n; i++) {
for(j=i; j < n; j++) {
printf(“%d”, j); // O(n^2)
}
}
常见的时间复杂度:
| 例子 | 时间复杂度 | 装逼术语 |
|---|---|---|
| 5201314 | O(1) | 常数阶 |
| 3n+4 | O(n) | 线性阶 |
| 3n^2+4n+5 | O(n^2) | 平方阶 |
| 3log(2)n+4 | O(logn) | 对数阶 |
| 2n+3nlog(2)n+14 | O(nlogn) | nlogn阶 |
| n3+2n2+4n+6 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
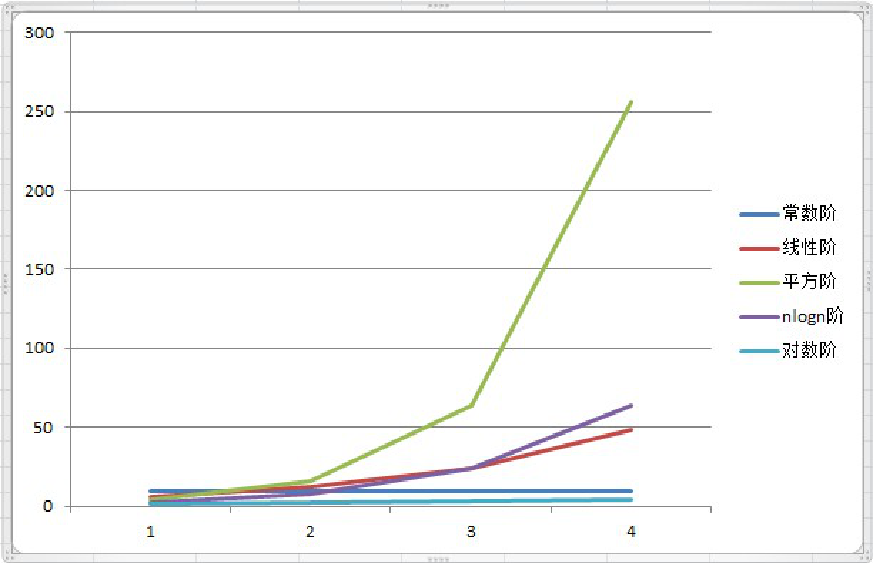
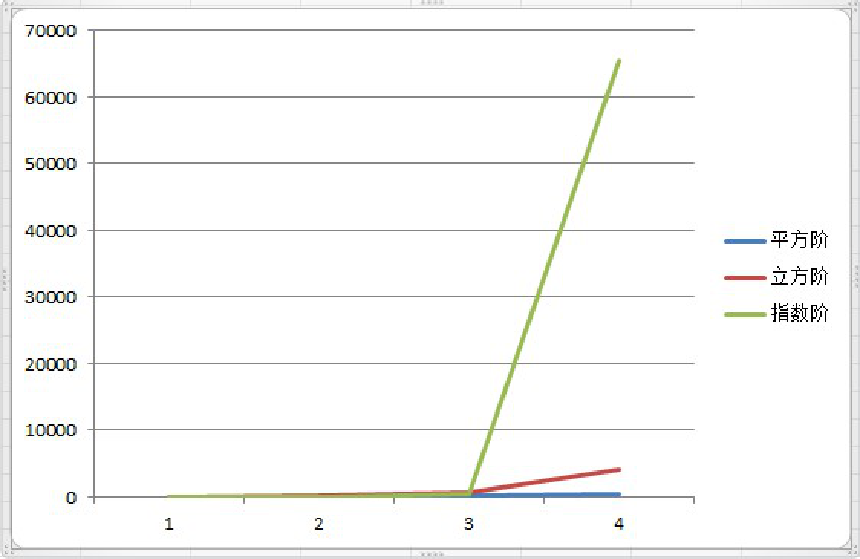
常用的时间复杂度所耗费的时间从小到大依次是:
O(1) < O(logn) < (n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
最坏情况与平均情况:
我们查找一个有n个随机数字数组中的某个数字,最好的情况是第一个数字就是,那么算法的时间复杂度为O(1),但也有可能这个数字就在最后一个位置,那么时间复杂度为O(n)。
平均运行时间是期望的运行时间。
最坏运行时间是一种保证。在应用中,这是一种最重要的需求,通常除非特别指定,我们提到的运行时间都是最坏情况的运行时间。
算法的空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法的空间复杂度的计算公式记作:S(n)=O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
通常,我们都是用“时间复杂度”来指运行时间的需求,是用“空间复杂度”指空间需求。
当直接要让我们求“复杂度”时,通常指的是时间复杂度。


