python——杨辉三角

1、定义：

 

 

2、基于定义打印

# -*- coding:utf-8 -*-
# version：python3.7

n = 6
triangle = [[1],[1,1]]
for i in range(2,n):     #已经给出前两行，所以求剩余行
    cur = [1]            #定义每行第一个元素
    pre = triangle[i-1]  #上一行
    for j in range(i-1): #算几次
        cur.append(pre[j] + pre[j+1])
    cur.append(1)
    triangle.append(cur)
print(triangle)

执行结果：
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1]]

# -*- coding:utf-8 -*-
# version：python3.7

n = 6
triangle = []
for i in range(n):
    cur = [1]
    triangle.append(cur)    #先追加进去
    if i == 0:
        continue
    pre = triangle[i-1]
    for j in range(i-1):
        cur.append(pre[j] + pre[j+1])
    cur.append(1)
print(triangle)

 

3、补0法打印

# -*- coding:utf-8 -*-
# version：python3.7

n = 6
triangle = [[1],[1,1]]
for i in range(2,n):
    newrow = triangle[i-1]
    newrow.append(0)
    row = [None] * (i+1)    #开辟空间
    for j in range(i+1):
        row[j] = newrow[j-1] + newrow[j]
    triangle.append(row)
print(triangle)

执行结果：
[[1], [1, 1, 0], [1, 2, 1, 0], [1, 3, 3, 1, 0], [1, 4, 6, 4, 1, 0], [1, 5, 10, 10, 5, 1]]

 

4、根据对称性打印（索引）

 

 

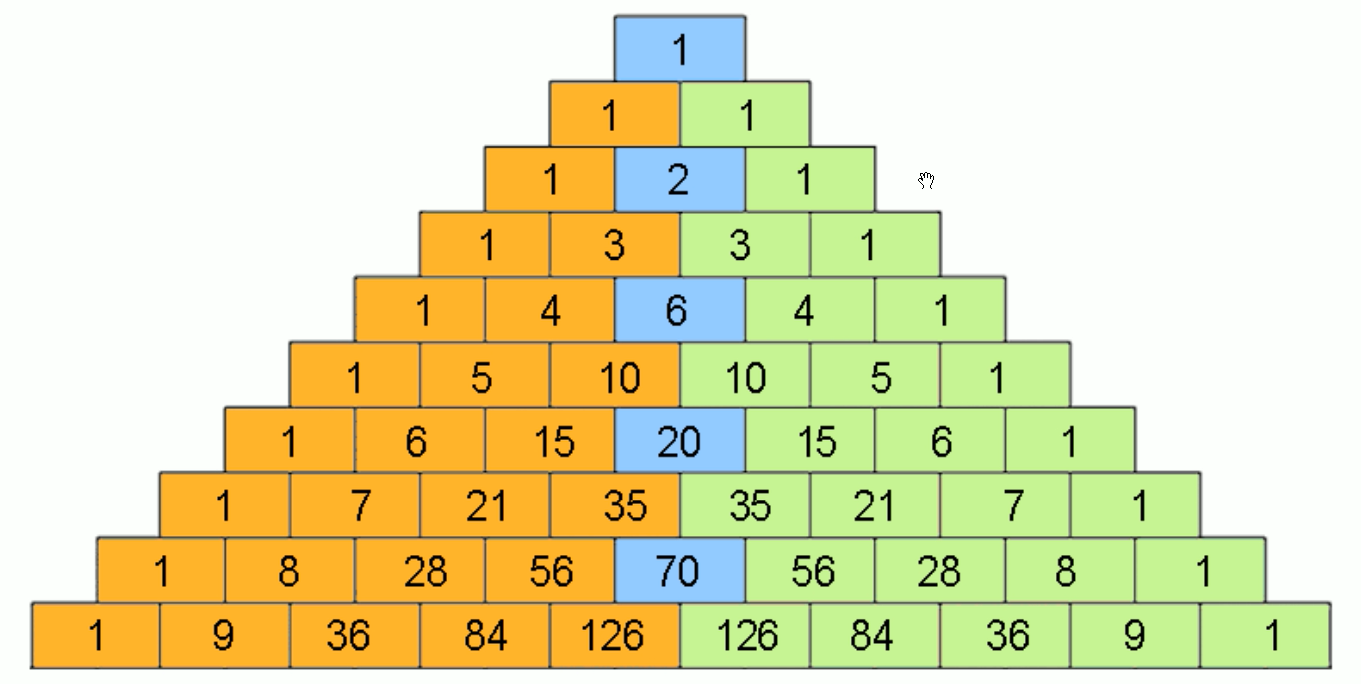
# -*- coding:utf-8 -*-
# version：python3.7

n = 6
triangle = [[1],[1,1]]
for i in range(2,n):
    row = [1] * (i+1)
    for j in range(i//2):    #有图知：大概的临界值为一半，再仔细推敲
        val = triangle[i-1][j] + triangle[i-1][j+1]
        row[j+1] = val
        row[i-j-1] =val      #此处规律：两个对称值的索引和等于 i
    triangle.append(row)
print(triangle)

执行结果：
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1]]

 

5、单个列表覆盖、切片完成

# -*- coding:utf-8 -*-
# version：python3.7

n = 6
row = [1] * n
for i in range(n):    #n行n次
    old = 1                  #old刚开始为1
    for j in range(i//2):
        val = old + row[j+1]
        old = row[j+1]    #此处现将row[j+1]的值赋给old，以防止被覆盖
        row[j+1] = val
        if i != 2*j:
            row[i-j-1] = val

　　print(row[:i+1])

执行结果：
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]