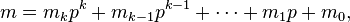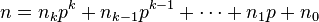[转]组合数取模 Lucas定理

对于C(n, m) mod p。这里的n，m，p（p为素数）都很大的情况。就不能再用C(n, m) = C(n - 1，m) + C(n - 1, m - 1)的公式递推了。

这里用到Lusac定理

For non-negative integers m and n and a prime p, the following congruence relation holds:

where

and

are the base p expansions of m and n respectively.

 

 对于单独的C(ni, mi) mod p，已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模，这里要用到m!(n-m)!的逆元。

根据费马小定理：

已知(a, p) = 1，则 a^p-1 ≡ 1 (mod p),  所以 a*a^p-2 ≡ 1 (mod p)。

也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)^{p-2 ；}

 

代码：

  #include <iostream>
  using namespace std;
  typedef long long LL;

LL exp_mod(LL a, LL b, LL p) {
    LL res = 1;
    while(b != 0) {
        if(b&1) res = (res * a) % p;
        a = (a*a) % p;
        b >>= 1;
    }
    return res;
}

LL Comb(LL a, LL b, LL p) {
    if(a < b)   return 0;
    if(a == b)  return 1;
    if(b > a - b)   b = a - b;

    LL ans = 1, ca = 1, cb = 1;
    for(LL i = 0; i < b; ++i) {
        ca = (ca * (a - i))%p;
        cb = (cb * (b - i))%p;
    }
    ans = (ca*exp_mod(cb, p - 2, p)) % p;
    return ans;
}

LL Lucas(int n, int m, int p) {
     LL ans = 1;

     while(n&&m&&ans) {
        ans = (ans*Comb(n%p, m%p, p)) % p;
        n /= p;
        m /= p;
     }
     return ans;
}

int main() {
    Read();
    int n, m, p;
    while(~scanf("%d%d%d", &n, &m, &p)) {
        printf("%lld\n", Lucas(n, m, p));
    }
    return 0;
}