python numpy库fft的问题记录

折腾了快一天，没想到真的是2pi的常数的问题。在这里记录一下。

按照wolfram的表述方式，如果采用normalization 1/√(2pi) oscillatory factor 1的fft，即FT表达式为：

\[\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} f(t) e^{i w t} d t \]

那么得到的在python中调用numpy得到的结果是完全错误的，例如对于均值滤波函数：

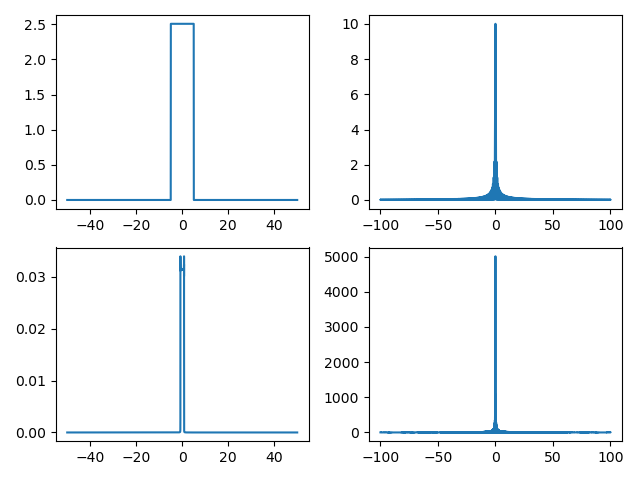
第一行两张图是在时域和频域的理论值，第二行是用第一行分别进行ifft和fft得到的时域和频域的计算值，可以看到高度和宽度都明显不对，用这个函数进行滤波再用np.fft.ifft变换回来的话就达不到滤波的效果。

正确的做法是用normalization 1 oscillatory factor -1的fft，即FT的表达式为：

\[\int_{-\infty}^{\infty} f(t) e^{-i w t} d t \]

个人感觉还挺微妙的...属于是定义体系不同吧，我看的论文用的其实看起来是normalization 1/2pi oscillatory factor -1的fft，仔细想的话就挺混乱的，不如直接写代码一种一种试x

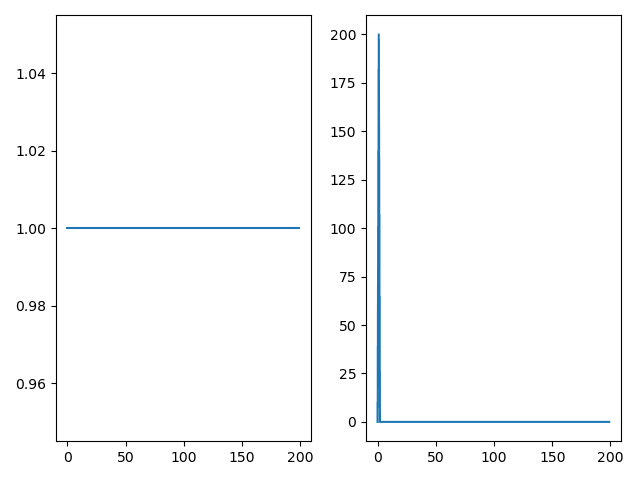
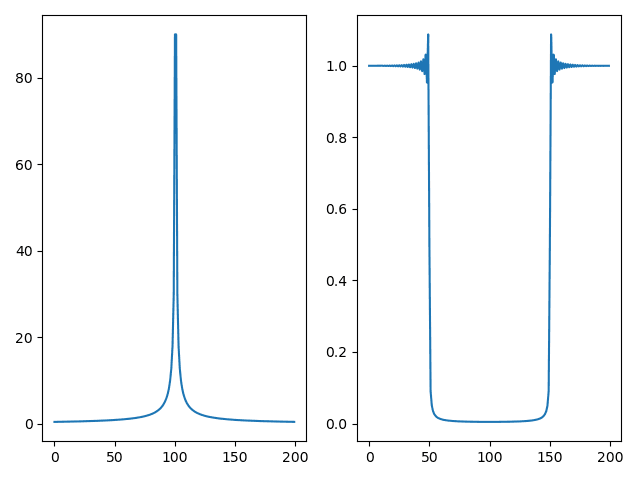
最后得到正确的脉冲函数和均值滤波函数的写法是：

点击查看代码

# 成功的脉冲函数
g=np.exp(-1j *2*np.pi* np.arange(200) / 200)
h=np.fft.ifft(g)
plt.figure(1)
plt.subplot(1, 2, 1)
plt.plot(abs(g))
plt.figure(1)
plt.subplot(1, 2, 2)
print(np.argmax(h))
plt.plot(abs(h))
plt.show()

# 成功的均值滤波函数
x=np.arange(200) / 200-0.5-1/400
x*=2*np.pi
A=100
g=A*np.sin(x*A/2)/(x*A/2)
h=np.fft.ifft(g)
plt.figure(1)
plt.subplot(1, 2, 1)
plt.plot(abs(g))
plt.figure(1)
plt.subplot(1, 2, 2)
print(np.argmax(h))
plt.plot(abs(h))
plt.show()

画图的结果是：