【CT】Filtered Backprojection原理（parallel-beam&fan-beam）

个人觉得讲得比较好的是这个ppt。然后会对物理原理做一点补充，加一点自己的理解。

物理原理

首先CT要解决的问题：

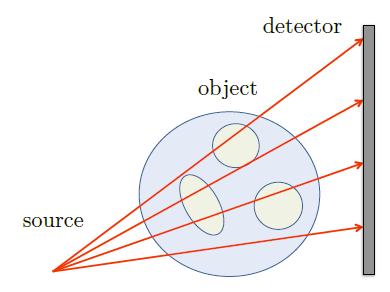
 已知光束和detector得到的平面图，求object信息。

物理学定律Beer‘s law：

$$\frac{d I}{d s}=-\mu(x(s)) I(s)$$

描述了光穿过物体的损耗，其中$\mu(x(s))$只与x(s)这个位置的物体性质有关，这也是我们要解的信息。对这个微分进行积分得到：

$$I_{x_{0}}(s)=I_{x_{0}}(0) e^{-\int_{0}^{s} \mu\left(x_{0}+\tau v\right) d \tau}$$

$$\log \left(\frac{I_{x_{0}}\left(\boldsymbol{x}_{\mathrm{out}}\right)}{I_{x_{0}}\left(\boldsymbol{x}_{\mathrm{in}}\right)}\right)=-\int_{s_{\mathrm{in}}}^{s_{\mathrm{out}}} \mu\left(x_{0}+\tau \boldsymbol{v}\right) d \tau$$

平行光束：

引入Radon变换：

$$\mathcal{R} f(t, \theta)=\int_{L_{t, \theta}} f(x) d S(x)=\iint f(x) \delta\left(\left\langle x, n_{\theta}\right\rangle-t\right) d x$$

含义解释：the integral of f along the line $L_{t,\theta}$ whose direction is perpendicular to $n_{\theta}$ and whose distance from the origin is t.

对它进行傅里叶变换可以发现：

$$\int \mathcal{R} f(t, \theta) e^{-i \omega t} d t=\hat{f}(\omega \cos \theta, \omega \sin \theta)$$

In other words, measuring the Radon transform is equivalent to acquiring the Fourier transform of f along radial lines.

这就是Central Slice Theorem，在ppt中解释得更形象：

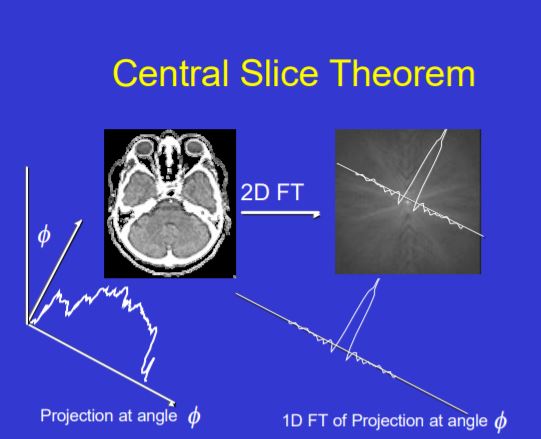
 The 1-D projection of the object, measured at angle $\phi$, is the same as the profile through the 2D FT of the object, at the same angle.

【在角度$\phi$的1D投影，和同一角度的2D傅里叶变换数值上相同】

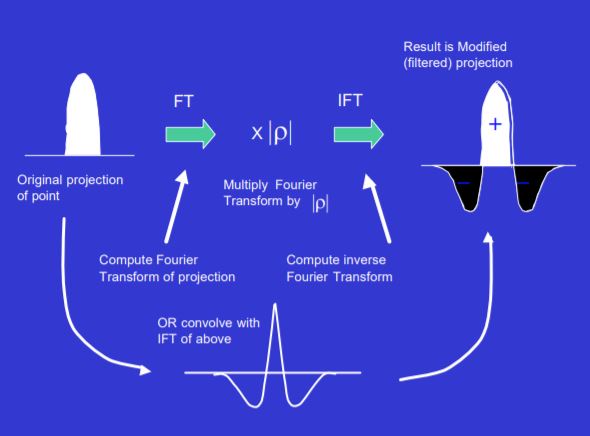
在此基础上定义filtered backprojection：

$$f(x)=\frac{1}{2 \pi} \int_{0}^{\pi}(\mathcal{R} f(\cdot, \theta) * h)\left(\left\langle x, n_{\theta}\right\rangle\right) d \theta$$

where h is such that $\hat{h}(\omega)=|\omega|$. 名字解释：we first filter the Radon transform along the radial variable with the convolution kernel h.

现实中我们获取数据时其实有把t和$\theta$都离散化，在傅里叶变换后等价于acquiring only a fraction of the radial lines，因此：

$$f_{\mathrm{rec}}(x) \approx \sum_{k}\left(\mathcal{R} f\left(\cdot, \theta_{k}\right) * h\right)\left(\left\langle x, n_{\theta_{k}}\right\rangle\right)$$

这一段也是ppt讲得更加清楚：

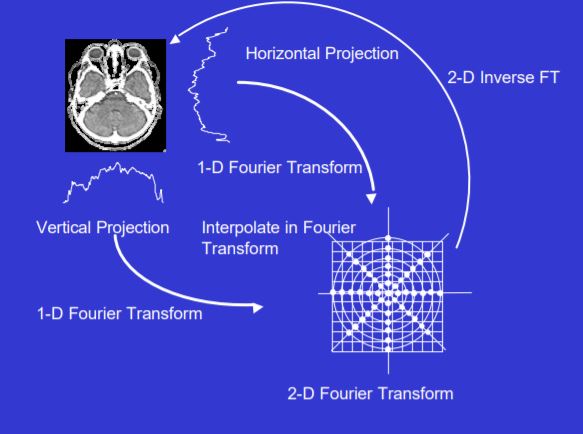
If all of the projections of the object are transformed like this, and interpolated into a 2-D Fourier plane, we can reconstruct the full 2-D FT of the object. The object is then reconstructed using a 2-D inverse Fourier Transform.

【把所有方向都这样变换，就可以把数值插值到2D傅里叶平面，从而构建整个的傅里叶信息，再用逆傅里叶变换得到原物体信息】

这是平行光束的情况，用网上找的代码流程帮助理解：

• 将原始投影进行一次一维傅立叶变换

• 设计合适的滤波器，在φi的角度下将得到原始投影p(x_r,φi)进行卷积滤波，得到滤波后的投影。

• 将滤波后的投影进行反投影，得到满足x_r=r cos⁡（(θ - φ_i)）方向上的原图像的密度。

• 将所有反投影进行叠加，得到重建后的投影。

其中滤波器的作用在ppt里面也有比较形象的解释：

 

 

扇形光束

对于扇形光束，转化为平行光束处理。首先介绍sinograph的概念：the 2-D array of data containing the projections，如果用平行光采集信息，角度为$\phi$ 距离为$\xi$，则平面$(\phi, \xi)$是这份数据的sinograph。事实上，我们完全可以把扇形光的sinograph调整为平行光情况，然后就可以按照平行光的算法处理：

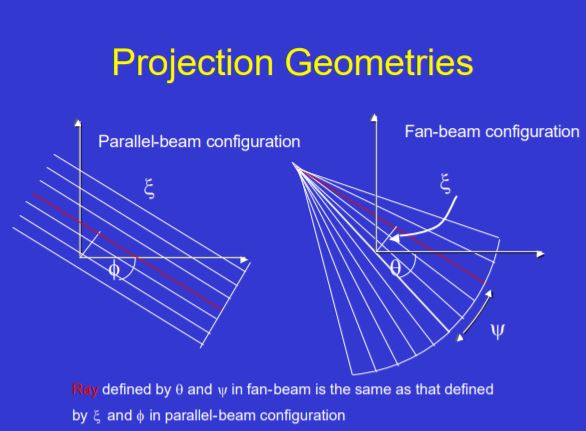
The red ray in both the parallel and diverging configurations are the same, and therefore occupy the same point in sinogram space.

需要调整的是1.角度的对应关系；2.距离的对应关系【和光的强度有关】。具体的公式就没推了。

 

学习CT相关的知识主要还是为了看懂下一篇博文要写的论文：Deep Learning Computed Tomography，这篇算是看论文前学的基础知识。