图卷积（变分）自编码器（GAE and VGAE）

    自编码器是无监督学习领域中一个非常重要的工具。最近由于图神经网络的兴起，图自编码器得到了广泛的关注。笔者最近在做相关的工作，对科研工作中经常遇到的：图自编码器（GAE）和图变分自编码器（VGAE）进行了总结。如有不对之处，请多多指正。

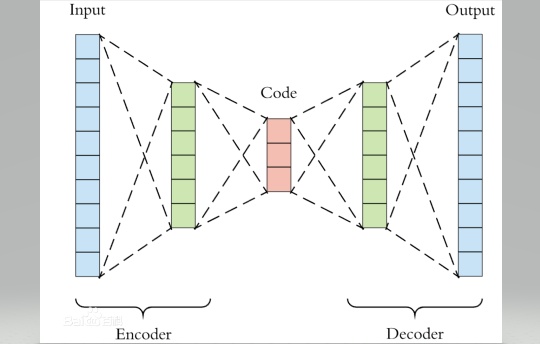
自编码器（AE）

    在解释图自编码器之前，首先理解下什么是自编码器。自编码器的思路来源于传统的PCA，其目的可以理解为非线性降维。我们知道在传统的PCA中，学习器学得一个子空间矩阵，将原始数据投影到一个低维子空间，从未达到数据降维的目的。自编码器则是利用神经网络将数据逐层降维，每层神经网络之间的激活函数就起到了将"线性"转化为"非线性"的作用。自编码器的网络结构可以是对称的也可以是非对称的。我们下面以一个简单的四层对称的自编码器为例，全文代码见最后。
   (严格的自编码器是只有一个隐藏层，但是我在这里做了个拓展，其最大的区别就是隐藏层以及神经元数量的多少，理解一个，其它的都就理解了。)

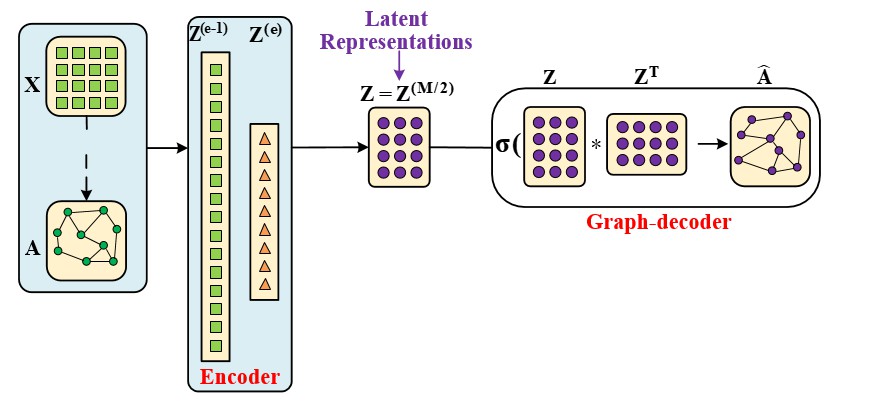
图自编码器（GAE）

    图自编码器和自编码器最大的区别有两点：一是图自编码器在encoder过程中使用了一个 \(n*n\) 的卷积核；另一个是图自编码器没有数据解码部分，转而代之的是图解码（graph decoder),具体实现是前后邻接矩阵的变化做loss。
   图自编码器可以像自编码器那样用来生成隐向量，也可以用来做链路预测（应用于推荐任务）。

变分自编码器（VAE）

   变分自编码是让中间层Z服从一个分布。这样我们想要生成一个新的样本的时候，就可以直接在特定分布中随机抽取一个样本。另外，我初学时遇到的疑惑，就是中间层是怎么符合分布的。我的理解是：
      输入样本：\(\mathbf{X \in \mathcal{R}^{n * d}}\)
      中间层 ：\(\mathbf{Z \in \mathcal{R}^{n * m}}\)
   所谓的正态分布是让\(Z\)的每一行\(z_i\)符合正态分布，这样才能随机从正态分布中抽一个新的\(z_i\)出来。

变分图自编码器（VGAE）

    如果你理解了变分比编码器和图自编码器，那么变分图自编码器你也就能理解了。第一个改动就是在VAE的基础上把encoder过程换成了GCN的卷积过程，另一个改动就是把decoder过程换成了图decoder过程。

   我在示例代码中，将这四种方法应用到下游任务中：聚类，分类，可视化。数据集和下游任务的代码见: https://github.com/zyx423/GAE-and-VGAE.git