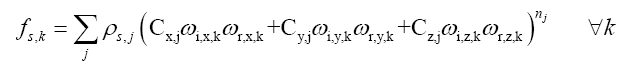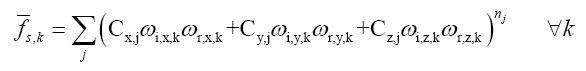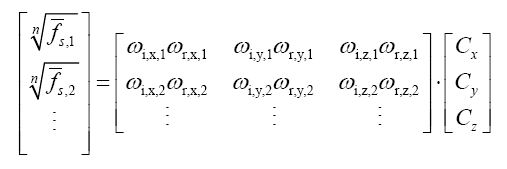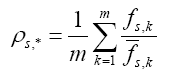sBRDF空间双向反射分布函数完全解析
SBRDF空间双向反射分布函数解析
声明:本文大部分内容基于Ph.D David K. McAllister的博士论文《A GENERALIZED SURFACE APPEARANCE REPRESENTATION FOR COMPUTER GRAPHICS》以及《GPU Gems1》里他的文章。如果有兴趣推荐大家研究博士论文原文,其中关于用相机对材质进行采样的一段非常有趣。我重构他的代码生成了一个简单的命令行工具可以从他的SVB格式中抽取出基本的纹理。他的代码用VC8编译有不少问题,我修复了大部分,主要是在库的链接以及C++的语法上,完全修复用VC6编译一次看看。马上又要考试了,再不看书要挂科了。
一、悉数光照模型
Phong光照模型是基于经验的局部光照模型,拥有漫反射Diffuse以及镜面反射Specular的效果,但是却省略了一切物理光学特性。可是目前的图形API和硬件都是按照Phong光照模型设计的。
Torrance et al.提出的Microfacet-Based Equation微平面公式模拟了大部分材质表面的特性。具体形式如下:

D代表任意一种分布函数,包括Gaussian分布函数或者是带指数项的Cos函数。
G是几何衰减系数,可以由表面被遮挡的程度或者是阴影来表示。(PS:Ambient Occlusion?)
F是菲涅尔Fresnel衰减系数。
MBE已经被Debevec et al.修正后用于人类皮肤模拟。
Ward 1992提出的Ward反射模型使用了椭圆型高斯锐化函数Elliptical Gaussian Sharpness Function在物体表面模拟了一个十字形的各项异性高光Anisotropic Highlights,可惜依旧不是基于物理特性的。(PS:有兴趣的朋友可以打开3dsmax等工具的材质编辑器试验一下)
二、Lafortune BRDF表达式的出现
BRDF使用若干个基本函数表现物体表面的光学特性。这些函数主要包括,spherical harmonics球面调和函数,spherical wavelets球面波,Zernike多项式。不过这些函数都不是专门为BRDF设计的。所以在使用BRDF时总是需要很多数据。一般来说50到200个系数才可以足够完美的表现。最麻烦的是,这些系数并不可以通过经验得来,必须要通过采集,所以设计一个通用的BRDF接口还很难做到。
下面是McAllister制作的采集装配:(PS:我想应该可以找个ARM单片机以及几个步进电机完成自动采集)
幸运的是,Lafortune, Foo et al. 1997引入了一个简单而十分有效的BRDF表达式,它的最大特点是用几个Lobe叶片就模拟了BRDF,而且最最重要的是,一切数值都可以简单得用纹理表示,所以现在我们可以简单的使用GPU进行实时渲染。入射向量以及反射向量都被转化到Local Coordinate局部坐标系中计算,避免了只有使用很多系数才能获得满意效果的窘境。还是让我们看一下Lafortune表达式:
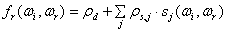
其中ρd是漫反射项,右边的求和式代表各种高光叶片Specular Lobe凸起形状的和,也就是表现了我们注视模型上那一点的时候所看到的高光形状。每一个叶片Lobej都有一个反照率ρs,j以及表达叶片形状Lobe Shape函数sj,还有最重要的入射出射向量ωi和ωr。Lobe Shape写成如下矩阵式:
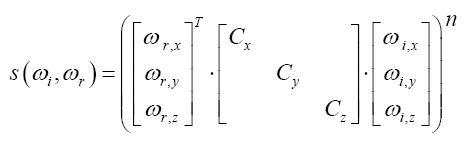
我们当然可以直接写成:
![]()
一切的“魔术”都在控制CxCyCz3个系数上。通过调整这三个系数,我们就可以实现各项异性Anisotropic材质表面的光照效果。
三、深入剖析
我把Ph.D McAllister叙述的sBRDF的计算方法总结归纳了一下。
ρd的计算比较繁琐。如果你安装了NVIDIA SDK 9.5,其中的HDR演示程序就使用了HDR Diffuse贴图。(PS:NVIDIA Geforce FX5900的演示程序Dawn里仙女皮肤表面的Diffuse项是通过计算法线与入射光夹角的余弦加权平均值计算得到的)。Lafortun与许多其他Image-Based基于图像的算法Pulli, Cohen et al. 1997; Rushmeier, Bernardini et al. 1998把这一项当作bi-directional reflectance samples双向反射样本的最小值:
![]()
fr,k是当前像素处第k个反射样本。
可是这仅仅是理论上的成立。真实情况下,用仪器测得的数据是会有错误的,因为我们无法保证样本总是完美的。Marschner (Marschner 1998)提出的方法就是上述被NVIDIA所使用的方法,其中的Weight权等于N•ωi与N•ωr的乘积。
有条件的朋友还可以这样:跑到室外选择一个场景,用多个曝光度拍摄环景照片,使用Paul Debevec的HDRShop在每个定角度对环境光的颜色和强度进行编码,创建漫反射查找表十字型Cube Map立方体贴图。
样图如下
然后让我们来处理求和式。当我们计算得到了ρd后,系统将每个Specular Lobe高光叶片形成的高光进行削减,下面的公式表现了这个操作。其中ωi,k和ωr,k依旧是入射和出射向量:
为了求得所有色彩通道都可以使用的数值,接下来,使用下式计算每一个luminance-weighted average of each fs,k经过亮度权调整过的fs,k的平均值:(PS:这是SONY Trinitron的数据,更加一般的系数是ITU HDTV标准 0.2125, 0.7154, 0.0721以及用于CRT显示器非线性色彩的0.299, 0.587, 0.114)
由于Lafortune表达式是一个非线性函数的叠加,所有的系数必须使用非线性方法进行重估。McAllister使用了Levenberg-Marquardt (L-M) method (Presse, Flannery et al. 1988),简称LM方法。(PS:具体L-M算法代码大家可以不必惊慌,我们可以用Tech-X Corporation的免费TxMath库。其中包含了L-M算法的实现,McAllister也使用了这个库。)
使用L-M需要一些已知的叶片系数。比如表现一个向前散射的叶片可以让Cx = -1,Cy=-1,Cz = 1,n = 10,向后散射叶片Cx=1,Cy=1,Cz=1,n=5。我们也可以使用随机的数值。
L-M还需要fs,k公式的Jacobian Matrix雅各比矩阵。计算方法如下:使用一个很小的Epsilon调整参数多次计算模型上的每一个点。由于计算时间过长,这部操作还无法变成图形软件中的插件使用与实时计算,只有预先离线计算好。McAllister指出这个优化方法非常适合一个或者两个叶片,更多的就不适合了。如果只有一个或者两个叶片预测的准确度高达90%以上。
如果我们不使用L-M方法,McAllister还展示了一个只针对于一个叶片的搜索方法。将fs,k写成这样,使用Brent Line Search搜索算法搜索:
返回使得误差数值最小的那一组Cx Cy Cz n。
啊哈,最后我们终于得到了镜面项:
四、渲染
首先我们需要准备一些材料,包括模型表面的N法向量,T切向量。(PS:曾经看过许多关于切线T的计算,无一例外的都是说可以简单的使用纹理st的方向代替,这对于部分UV贴图的简单模型可能管用,但是对于复杂的有凹的物体来说肯定是不正确的)。T切向量的计算方式如下,假设一个三角形由3个顶点坐标P0 P1 P2和3个纹理坐标<s0,t0> <s1,t1> <s2,t2>:
如何使用Tangent呢?对于NVIDIA Geforce6系列后的显卡你可以尝鲜使用Vertex Texture,Ati Radeon X1000系列的卡可以使用R2VB,或者更加直接的使用Vertex Attribute传入Shader。至于Binormal你可以直接在Vertex Shader中使用cross叉乘得到。
GPU GEMS 上他展示的是Cg Shader,这里我把它改成了GLSL的。等我完成了一个GL基础库后放上DEMO。
这是Fragment Shader:
#define NUM_LOBES 2
#define SCL (1.0 / (96.0 / 256.0))
#define BIAS (SCL / 2.0)
#define EXSCL 255.0
uniform float Expos;
uniform sampler2D Diffus;
uniform sampler2D LobeShape[NUM_LOBES];
uniform sampler2D Albedo[NUM_LOBES];
uniform samplerCube EnvDiffuse;
uniform samplerCube EnvSpec;
varying vec2 TexUV;//Texcoords
varying vec3 EyeVec;//Vector to Eye in Local Space
varying vec3 TanVec;//Tangent In World Space
varying vec3 NrmVec;//Normal In World Space
varying vec3 BinVec;//Binormal In World Space
vec3 f3texCUBE_RGBE(samplerCube map,vec3 N)
{
vec4 rgbe = textureCube(map,N);
float f = ldexp(1.0,rgbe.w - 136.0);
return vec3(rgbe*f);
//return vec3(0.0,0.0,0.0);
}
vec3 f3texCUBE_RGBE_Conv(samplerCube map,vec3 normal,float N)
{
vec4 rgbe = textureCubeLod(map,normal,N);
float f = ldexp(1.0,rgbe.w - 136.0);
return vec3(rgbe*f);
}
vec3 ApplyLobe(vec3 toeye,vec4 lobeshape,vec3 lobealbedo,vec3 T,vec3 B,vec3 N,samplerCube tex_s)
{
vec3 Cwr_local = lobeshape.xyz * toeye;
//transform lobe peak in world space
/*
TBN Matrix
Tx Ty Tz
Bx By Bz
Nx Ny Nz
TBN InverseMatrix just is
Tx Bx Nx
Ty By Ny
Tz Bz Nz
Cwr_world.x = dot( vec3(T.x,B.x,N.x), Cwr_local);
*/
mat3 TBNMatrixInverse = mat3(T,B,N);
vec3 Cwr_world = Cwr_local*TBNMatrixInverse;
float sharpness = lobeshape.w;
vec3 incrad = f3texCUBE_RGBE_Conv(tex_s,Cwr_world,sharpness);
float lobelen = pow(dot(Cwr_world,Cwr_world),sharpness*0.5);
vec3 irrad = incrad*(Cwr_local.z*lobelen);
vec3 radiance = irrad*lobealbedo;
return radiance;
}
void main()
{
vec4 lobe_shape[NUM_LOBES];
vec4 lobe_albedo[NUM_LOBES];
for(int p=0; p<NUM_LOBES; p++){
lobe_shape[p] = texture2D(LobeShape[p],TexUV.st) + vec4(SCL,SCL,SCL,EXSCL) - vec4(BIAS,BIAS,BIAS,0.0);
lobe_albedo[p] = texture2D(Albedo[p],TexUV.st);
}
vec4 diff_albedo = texture2D(Diffus, TexUV.st);
vec3 exrad = vec3(0.0,0.0,0.0);
for(int l = 0;l<NUM_LOBES; l++){
exrad += ApplyLobe(EyeVec,lobe_shape[l],lobe_albedo[l].xyz,TanVec,BinVec,NrmVec,EnvSpec);
}
vec3 irrad = f3texCUBE_RGBE(EnvDiffuse,NrmVec);
exrad += (diff_albedo.xyz*irrad);
vec4 final_color = vec4(exrad*Expos,diff_albedo.w);
gl_FragColor = final_color;
}
来自sBRDF网站的样本图片:

原文以及相关的资料大家可以在这里找到:
http://sbrdf.cs.unc.edu/index.html
我编译好的命令行工具以及一个SVB样本: http://webdisk.cech.com.cn/download/file_share_3252301.html