雾雨魔理沙 (Standard IO)
Description
在幻想乡,雾雨魔理沙是住在魔法之森普通的黑魔法少女。话说最近魔理沙从香霖堂拿到了升级过后的的迷你八卦炉,她迫不及待地希望试试八卦炉的威力。在一个二维平面上有许多毛玉(一种飞行生物,可以视为点),每个毛玉具有两个属性,分值value和倍率mul。八卦炉发射出的魔法炮是一条无限长的直线形区域,可以视为两条倾斜角为α的平行线之间的区域,平行线之间的距离可以为任意值,如下图所示:
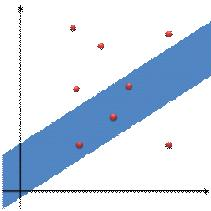
蓝色部分上下两条长边之间就是这次八卦炉的攻击范围,在蓝色范围内的毛玉(红点)属于该此被击中的毛玉,如果一个毛玉刚好在边界上也视为被击中。毛玉击中以后就会消失,每次发射八卦炉得到分值是该次击中毛玉的分值和乘上这些毛玉平均的倍率,设该次击中的毛玉集合为S,则分值计算公式为:
Score = SUM{value[i] | i 属于 S} * SUM{mul[i] | i 属于 S} / |S|
其中|S|表示S的元素个数。魔理沙将会使用若干次八卦炉,直到把所有毛玉全部击中。任意两次攻击的范围均不重叠。最后得到的分值为每次攻击分值之和。现在请你计算出能够得到的最大分值。
Input
第1行:1个整数N,表示毛玉个数
第2..N+1行:每行四个整数x, y, value, mul,表示星星的坐标(x,y),以及value和mul
第N+2行:1个整数α,表示倾斜角角度,0°到180°
Output
第1行:1个实数,表示最大分值,保留三位小数
题解
先求出那直线的一次函数,怎么求?经过证明,tan(a)就是y=kx+b的k。然后自己DP找最大值咯。
代码
uses math;
var
n:longint;
x,y,va,mul,sv,sm:array [0..2001] of longint;
b,f:array [0..2001] of real;
m:real;
procedure qsort(l,r:longint);
var
i,j,t:longint;
tt,m:real;
begin
i:=l; j:=r;
m:=b[(l+r) div 2];
repeat
while b[i]>m do inc(i);
while b[j]<m do dec(j);
if i<=j then
begin
tt:=b[i]; b[i]:=b[j]; b[j]:=tt;
t:=x[i]; x[i]:=x[j]; x[j]:=t;
t:=y[i]; y[i]:=y[j]; y[j]:=t;
t:=va[i]; va[i]:=va[j]; va[j]:=t;
t:=mul[i]; mul[i]:=mul[j]; mul[j]:=t;
inc(i); dec(j);
end;
until i>j;
if l<j then qsort(l,j);
if i<r then qsort(i,r);
end;
procedure init;
var
i:longint;
begin
readln(n);
for i:=1 to n do
readln(x[i],y[i],va[i],mul[i]);
readln(m);
m:=tan(m*PI()/180);
for i:=1 to n do
b[i]:=y[i]-m*x[i];
qsort(1,n);
end;
procedure main;
var
i,j:longint;
begin
for i:=1 to n do
begin
sv[i]:=sv[i-1]+va[i];
sm[i]:=sm[i-1]+mul[i];
end;
b[0]:=123567891011121;
f[1]:=va[1]*mul[1];
for i:=2 to n do
for j:=0 to i-1 do
if b[i]<>b[j] then //可能有精度问题。
f[i]:=max(f[i],f[j]+(sv[i]-sv[j])*((sm[i]-sm[j])/(i-j)));
write(f[n]:0:3);
end;
begin
init;
main;
end.

