砍树 (Standard IO)
Description
给出一个树形图(“tree-shaped” network),有N(1 <= N <= 10,000)个顶点。如果删除树上某一个顶点,整棵树就会分割成若干个部分。显然,每个部分内部仍保持连通性。
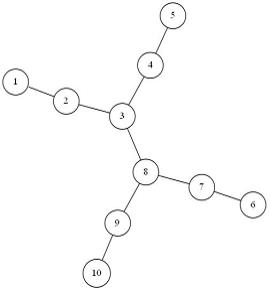
现在问:删除哪个点,使得分割开的每个连通子图中点的数量不超过N/2。如果有很多这样的点,就按升序输出。
例如,如图所示的树形图,砍掉顶点3或者顶点8,分割开的各部件。
Input
第1行:1个整数N,表示顶点数。顶点编号1~N
第2..N行:每行2个整数X和Y,表示顶点X与Y之间有一条边
Output
若干行,每行1个整数,表示一个符合条件的顶点的编号。如果没有顶点符合条件,则仅在第1行上输出”NONE”
题解
刚开始看这题,这TM不是割点吗?看了题解后,TM居然是dfs,呜呜呜…
直接dfs,找到一个入度为1的点作为根节点,dfs一下用f[i]记录i节点的儿子个数
枚举要删的点,分别统计它的子节点、父节点形成的连通块节点数量,判断一下就好了。至于‘NONE’情况,它请假回家了。
代码
type
arr=record
x,y,next:longint;
end;
var
n,root:longint;
a:array [0..40001] of arr;
v:array [0..10001] of boolean;
ls,bo,f:array [0..10001] of longint;
procedure dfs(x:longint);
var
i:longint;
begin
v[x]:=true;
if (bo[x]=1) and (x<>root) then
begin
f[x]:=1;
exit;
end;
i:=ls[x];
while i<>0 do
begin
if not v[a[i].y] then
begin
dfs(a[i].y);
f[x]:=f[x]+f[a[i].y];
end;
i:=a[i].next;
end;
inc(f[x]);
end;
procedure init;
var
i,o,p:longint;
begin
fillchar(bo,sizeof(bo),0);
readln(n);
n:=n-1;
for i:=1 to n do
begin
readln(o,p);
with a[i] do
begin
x:=o; y:=p;
next:=ls[x];
ls[x]:=i;
end;
with a[i+n] do
begin
x:=p; y:=o;
next:=ls[x];
ls[x]:=i+n;
end;
inc(bo[o]); inc(bo[p]);
end;
n:=n+1;
for i:=1 to n do
if bo[i]=1 then
begin
root:=i;
break;
end;
end;
procedure print;
var
i,j:longint;
boo:boolean;
begin
for i:=1 to n do
begin
boo:=true;
j:=ls[i];
while j<>0 do
begin
if (f[a[j].y]<f[i]) and (f[a[j].y]>n div 2) then
boo:=false;
j:=a[j].next;
end;
if (boo) and (n-f[i]<=n div 2) then
writeln(i);
end;
end;
begin
init;
dfs(root);
print;
end.


