uva10943(隔板法)
很裸的隔板法。
引用一下维基上对隔板法的解释:
现在有10个球,要放进3个盒子里
- ●●●●●●●●●●
隔2个板子,把10个球被隔开成3个部份
- ●|●|●●●●●●●●、●|●●|●●●●●●●、●|●●●|●●●●●●、●|●●●●|●●●●●、●|●●●●●|●●●●、●|●●●●●●|●●●、......
如此类推,10个球放进3个盒子的方法总数为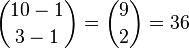
n个球放进k个盒子的方法总数为
问题等价于求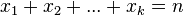 的可行解数,其中
的可行解数,其中 为正整数。
为正整数。
**如果允许有空盒子**:
现在有10个球,要放进3个盒子里,并允许空盒子。考虑10+3个球的情况:
- ●|●|●●●●●●●●●●●
从3个盒子里各拿走一个,得到一种情况,如此类推:
- ||●●●●●●●●●●、|●|●●●●●●●●●、|●●|●●●●●●●●、|●●●|●●●●●●●、|●●●●|●●●●●●、......
n个球放进k个盒子的方法总数(允许空盒子)为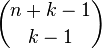 [2]
[2]
问题等价于求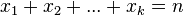 的可行解数,其中
的可行解数,其中 为非负整数。
为非负整数。
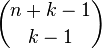 也是
也是 展开式的项数,这是因为展开后每一项肯定是a1^x1*a2^x2*......*ak^xk,而且x1+x2+...+xk=n.那就转化为上面那个问题了。
展开式的项数,这是因为展开后每一项肯定是a1^x1*a2^x2*......*ak^xk,而且x1+x2+...+xk=n.那就转化为上面那个问题了。
另一种变形:
减少球数用隔板法
将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,求放法总数。
分析:先在编号1,2,3,4的四个盒子内分别放0,1,2,3个球,剩下14个无区别的球,问题等价于将14个球放入4个编号为1,2,3,4的四个盒子里,每个盒子至少有一个球的问题。
剩下14个无区别的球排成一列,共形成13个空,可以理解为有3块隔板,将排成一列的球隔成4段,每段至少1个,有C3/13=286(种)。
如果不用隔板法,亦可以递推来做:
按最后一个加上的数是几来分类,ans[n][k]=ans[n-1][k]+ans[n][k-1].其中ans[n][k-1]是最后一个加0,ans[n-1][k]是最后一位加的不是0.
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<stack>
#include<queue>
using namespace std;
#define INF 1000000000
#define eps 1e-8
#define pii pair<int,int>
#define LL long long int
const int mod=1000000;
int n,k,ans,c[250][250];
int main()
{
//freopen("in6.txt","r",stdin);
//freopen("out.txt","w",stdout);
c[0][0]=1;
for(int i=1;i<=200;i++)
{
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++)
{
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
while(scanf("%d%d",&n,&k)==2)
{
if(n==0&&k==0) break;
else
{
printf("%d\n",c[n+k-1][k-1]);
}
}
//fclose(stdin);
//fclose(stdout);
return 0;
}


